elastictube1d: A C++ repository from preCICE

title	permalink	keywords	summary
1D Elastic Tube	https://www.precice.org/tutorials-elastic-tube-1d.html	OpenFOAM, python	The 1D Elastic Tube is a FSI case, that consists of an internal flow in a flexible tube. The flow is unsteady and incompressible. This tutorial contains C++ and Python variants of the fluid and solid solvers. Running the simulation takes just 1-2 minutes.

Setup

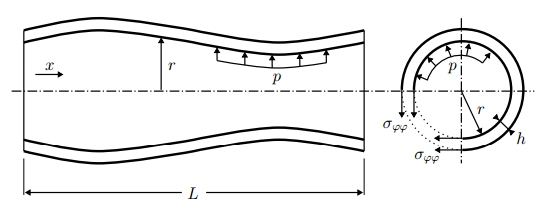
We want to simulate the internal flow in a flexible tube as shown in the figure below (image from [1]).

The flow is assumed to be incompressible flow and gravity is neglected. Due to the axisymmetry, the flow can be described using a quasi-two-dimensional continuity and momentum equations. The motivation and exact formulation of the equations that we consider can be found in [2].

The following parameters have been chosen:

Length of the tube: L = 10
Inlet velocity: $$ v_{inlet} = 10 + 3 sin (10 \pi t) $$
Initial cross sectional area = 1
Initial velocity: v = 10
Initial pressure: p = 0
Fluid density: $$ \rho = 1 $$
Young modulus: E = 10000

Available solvers

Both fluid and solid participant are supported in:

C++: An example solver using the intrinsic C++ API of preCICE. This solver also depends on LAPACK (e.g. on Ubuntu sudo apt-get install liblapack-dev)
Python: An example solver using the preCICE Python bindings. This solver also depends on the Python libraries numpy scipy matplotlib vtk mpi4py, which you can get from your system package manager or with pip3 install --user <package>.

Building the C++ Solver

In order to use the C++ solver, you first need to build the scripts FluidSolver and SolidSolver. Each script needs to be built separately.

cd fluid-cpp
mkdir build && cd build
cmake ..
make all

cd solid-cpp
mkdir build && cd build
cmake .. 
make all

Building can be skipped if you do not plan to use the C++ version.

Running the Simulation

C++

Open two separate terminals and start each participant by calling the respective run script.

cd fluid-cpp
./run.sh
# or, in parallel: ./run.sh -parallel

and

cd solid-cpp
./run.sh

The run scripts set the input parameters N = 100, tau = 0.01, kappa = 100.

{% include warning.html content= "Running serial or parallel leads to different results. Please refer to this open issue for more insight" %}

Python

Open two separate terminals and start each participant by calling the respective run script. Only serial run is possible:

cd fluid-python
./run.sh

and

cd solid-python
./run.sh

Parameters such as N can be modified directly at the FluidSolver.py and at the SolidSolver.py. The parameters must be consistent between the different solvers and participants.

Optional: Visualization and video output of the fluid participant can be triggered via the options --enable-plot and --write-video of FluidSolver.py. To generate .vtk files during execution, you need to add the flag --write-vtk.

{% include warning.html content= "The cpp and python solvers lead to different results. Please consider the Python results as the correct ones and refer to this open issue for more insight" %}

Post-processing

The postproc/ folder contains the .vtk files resulting from the execution, which you can visualize using eg. paraview. Alternatively you can visualize the results with the provided postproc/plot-fluid.py script:

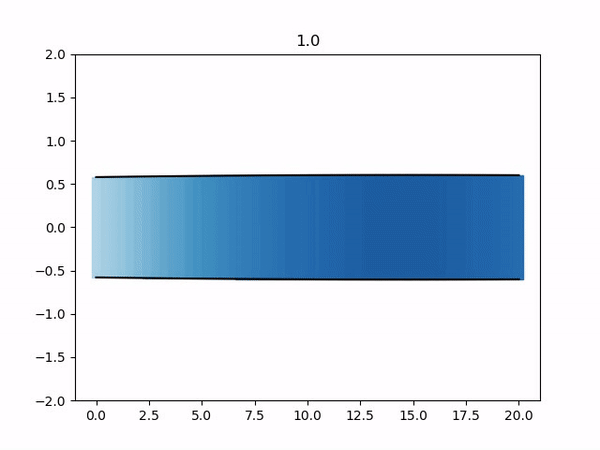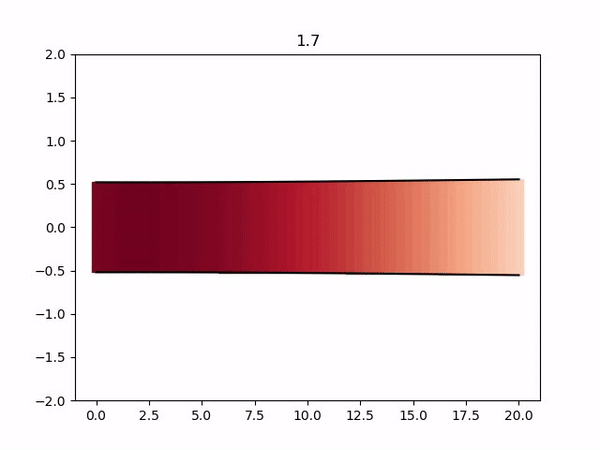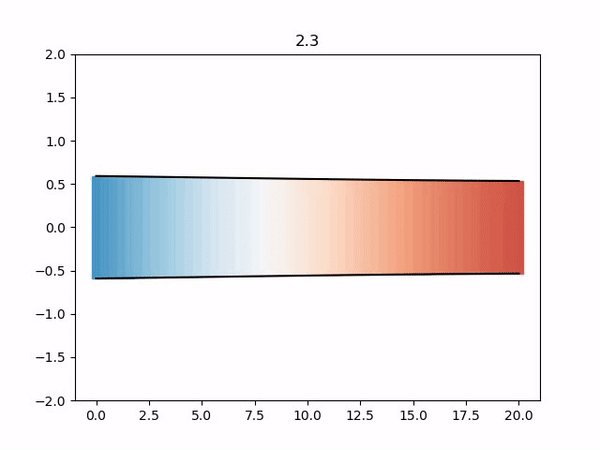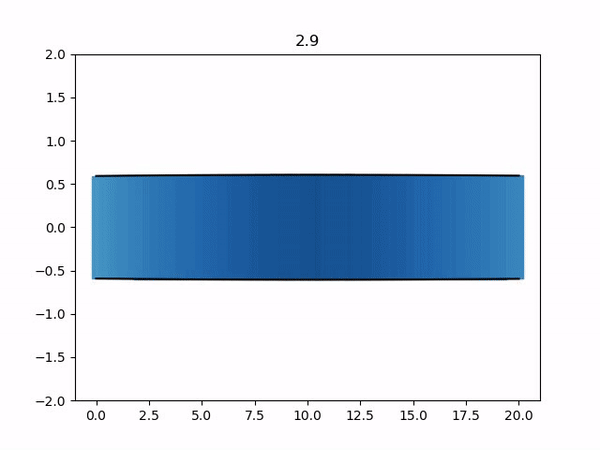
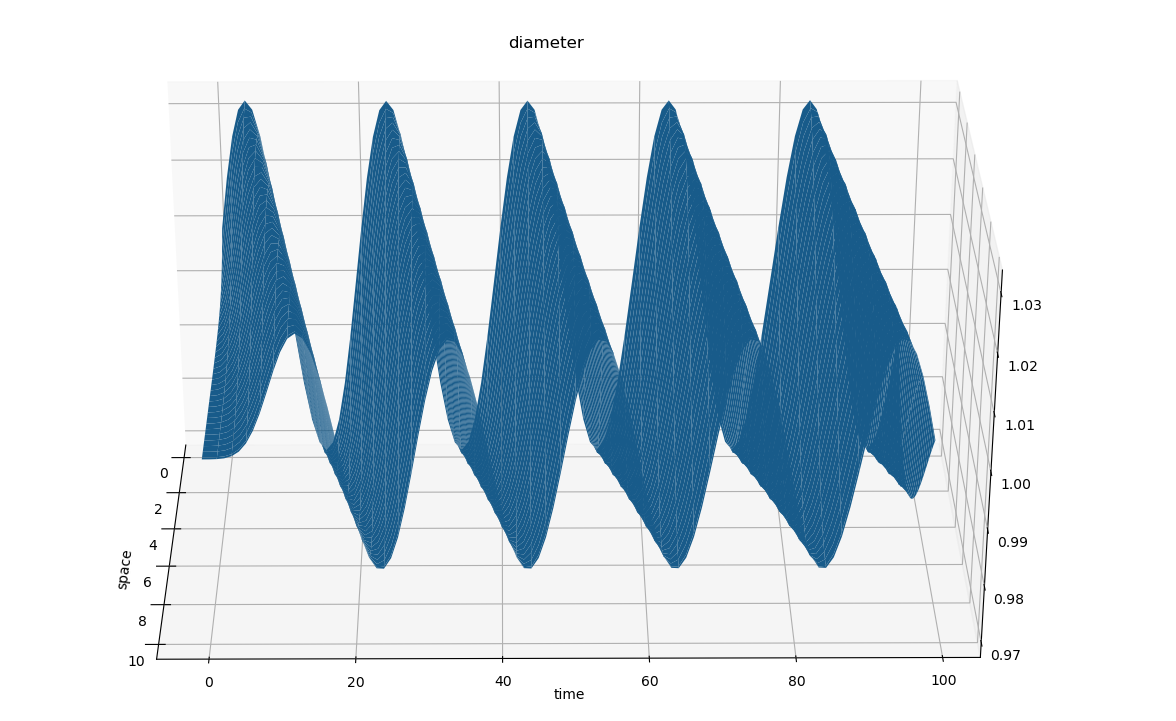
$ python3 postproc/plot-fluid.py <quantity> postproc/<prefix>

Note the required arguments specifying which quantity to plot (pressure, velocity or diameter) and the name prefix of the target vtk files.

For example, to plot the diameter using the default prefix for vtk files, we execute:

$ python3 postproc/plot-fluid.py diameter postproc/out_fluid_

If you run the case in parallel, you can visualize the results calculated by one rank (eg. rank 0) as follows:

$ python3 postproc/plot-fluid.py diameter postproc/out_fluid0_

References

[1] B. Gatzhammer. Efficient and Flexible Partitioned Simulation of Fluid-Structure Interactions. Technische Universitaet Muenchen, Fakultaet fuer Informatik, 2014.

[2] J. Degroote, P. Bruggeman, R. Haelterman, and J. Vierendeels. Stability of a coupling technique for partitioned solvers in FSI applications. Computers & Structures, 2008.

[3] M. Mehl, B. Uekermann, H. Bijl, D. Blom, B. Gatzhammer, and A. van Zuijlen. Parallel coupling numerics for partitioned fluid-structure interaction simulations. CAMWA, 2016.

precice/elastictube1d