Patricio R Estevez-Soto. Actualizado: 2020-04-06 01:06:02 GMT
Este proyecto no está siendo actualizado
Visita esta página para más información.
Si te interesa dar seguimiento a otros proyectos de seguimiento del covid-19 en México te recomiendo los siguientes sitios:
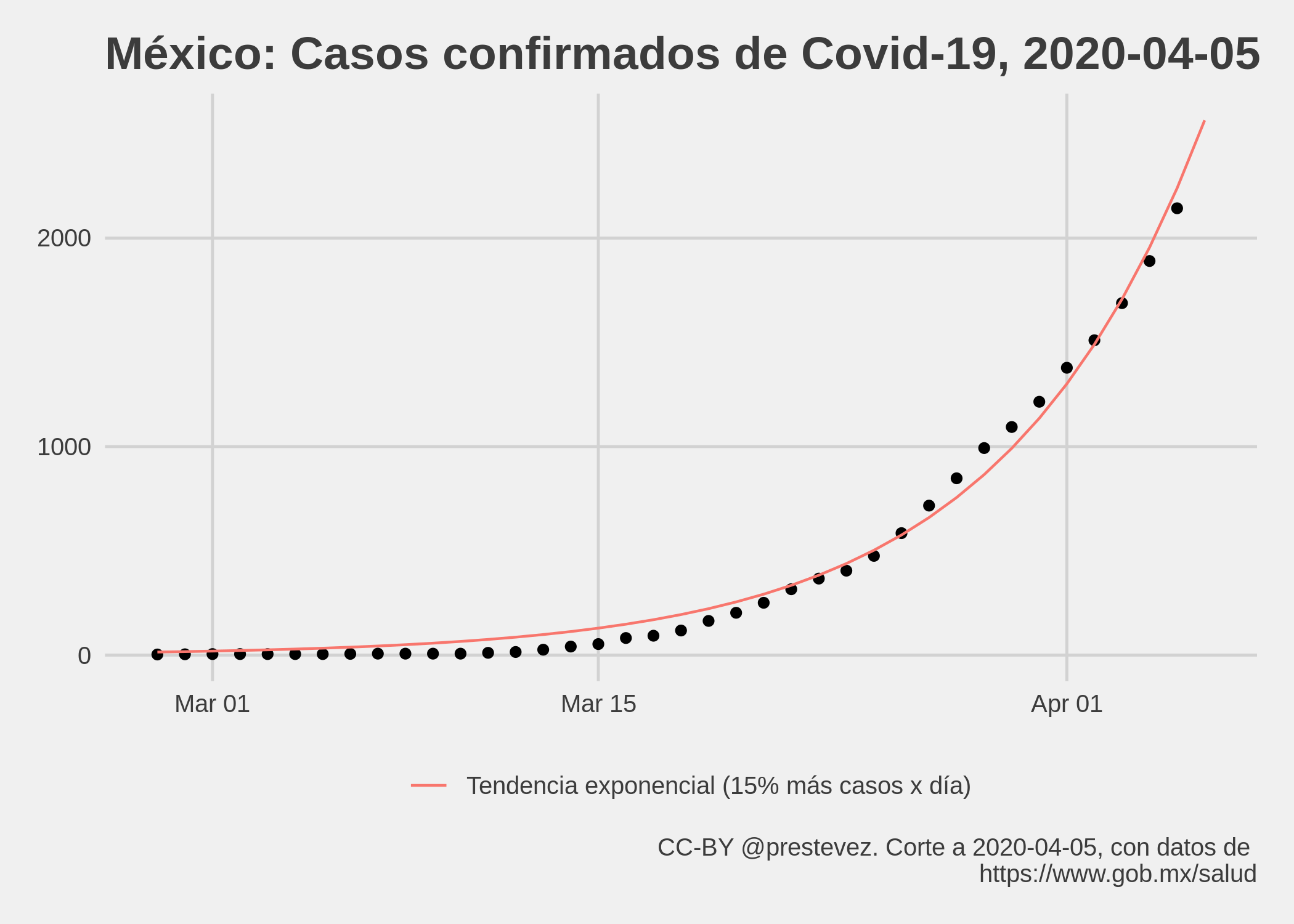
Gráfica con evolución de casos confirmados de Covid-19 en México. Datos originales tomados de la página de la Secretaría de Salud.
La gráfica muestra también una linea de tendencia calculada con un modelo exponencial:
E[casos | dia] = eb0 + b x dia
La gráfica presenta una extrapolación de la línea de tendencia indicando cuantos casos habría en un día asumiendo que la tendencia se mantiene. Sin embargo, es importante notar que los datos tienen un gran sesgo de medición, pues representan solamente los casos detectados—los cuales variarán en función de la cantidad de pruebas realizadas y verificadas por la autoridad sanitaria. Por tanto, es muy probable que el modelo predictivo contenga errores importantes y que los casos detectados sean menores (o mayores) a los esperados.
Considerando las limitaciones de los datos, los resultados del modelo no deben de considerarse como predicciones robustas. Son aproximaciones ingenuas para dar una idea general de cómo podría evolucionar el fenómeno con base en los datos existentes.
Parámetros del modelo predictivo:
##
## Call:
## glm(formula = casos ~ t, family = gaussian("log"), data = casos)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -96.33 -62.83 -30.22 -13.25 127.21
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.555234 0.124780 20.48 <2e-16 ***
## t 0.135755 0.003566 38.06 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 3603.66)
##
## Null deviance: 13837387 on 37 degrees of freedom
## Residual deviance: 129726 on 36 degrees of freedom
## AIC: 422.99
##
## Number of Fisher Scoring iterations: 6
Los errores estándar calculados en el modelo exponencial son erróneos. Esto es porque, especialmente para los casos acumulados, pero para para muchos datos en serie de tiempo los modelos no son independientes entre sí (hay autocorrelación en el tiempo) y no están identicamente distribuidos. Por ello, los errores no cumplen con los supestos básicos del modelo y no son confiables.
Hay varias maneras de obtener errores robustos. Una de ella es usar el método Jackknife. Esto implica calcular la línea de tendencia n veces omitiendo secuencialmente una observación del índice 1 a n de cada cáclulo. Ello nos da una distribución más robusta del valor esperado del estimador de la tendencia.
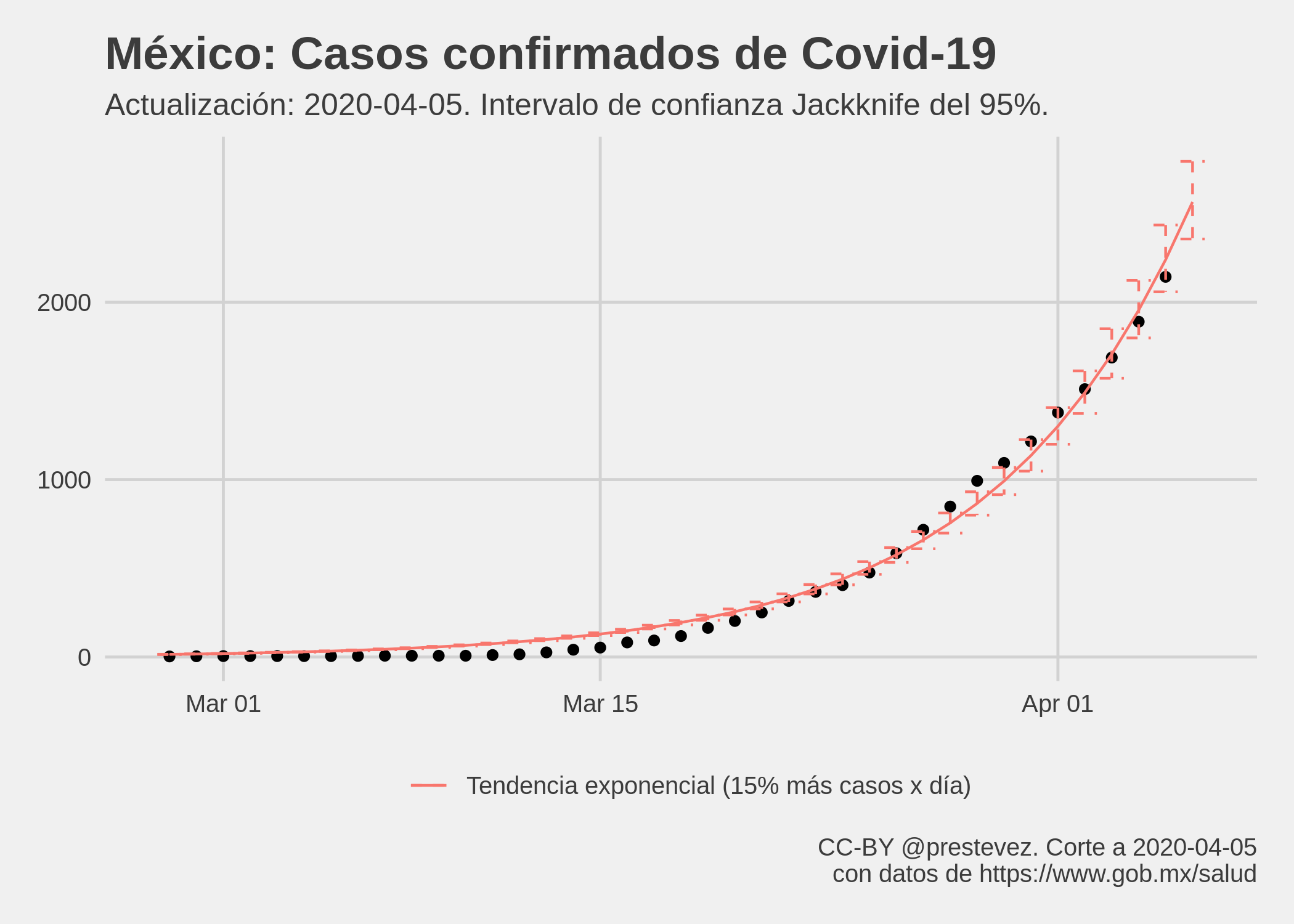
Gráfica con evolución del total de casos confirmados de Covid-19 en México con errores Jackknife.
El Jackknife no es la única forma de obtener errores robustos. En es caso decidí usar el Jackknife para controlar el sesgo por errores de muestreo y controlar el efecto de observaciones fuera de rango (outliers). De nuevo, este no es un modelo epidemiológico y las predicciones no son robustas.
Parámetros Jackknife del modelo predictivo de casos:
## # A tibble: 2 x 4
## var Estimate ci_low ci_high
## <chr> <dbl> <dbl> <dbl>
## 1 (Intercept) 2.55 2.50 2.58
## 2 t 0.136 0.135 0.137
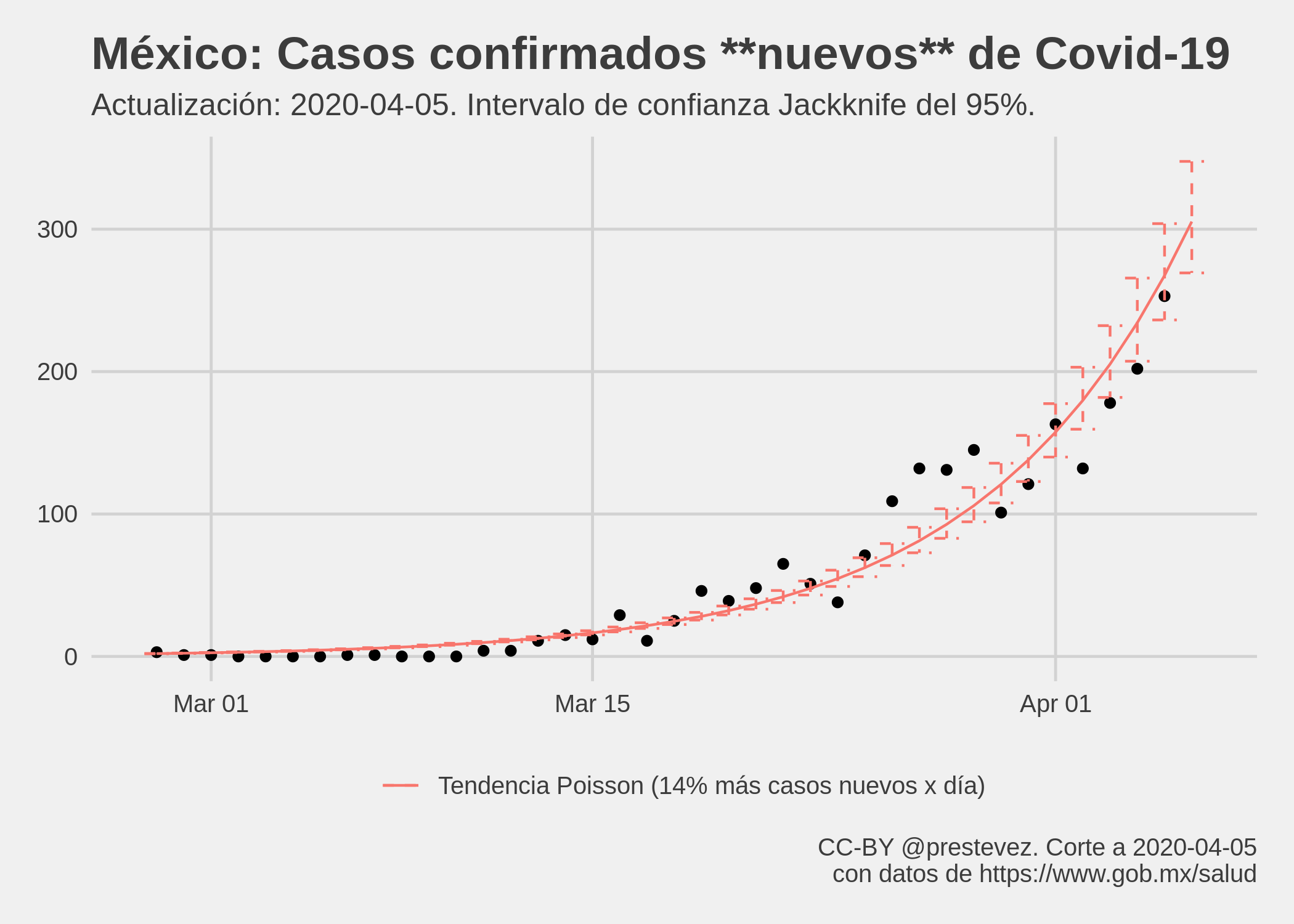
El modelo exponencial del acumulado de casos confirmados de Covid-19 es problemático pues las observaciones son monotónicas (solo pueden permanecer igual o crecer) y presentan una fuerte correlación temporal (el total de hoy es el total de ayer más los casos de hoy). Por tanto, se recomienda analizar el conteo de casos nuevos en lugar de usar el total de casos confirmados.
Para ello utilicé un modelo Poisson (un modelo apropiado para modelar conteos de eventos discretos) asumiendo que la tasa de ocurrencia de casos nuevos varía exponencialmente con el tiempo (según el modelo Poisson estándar). Asimismo, utilicé errores estándar Jackknife para calcular un intervalo de confianza del 95%.
De nuevo, es importante recordar que este modelo no es robusto ni busca modelar el curso de la epidemia, es simplemente una aproximación al patrón de crecimiento que han seguido los casos reportados de Covid-19.
Parámetros del modelo predictivo de casos nuevos:
##
## Call:
## glm(formula = casos_nuevos ~ t, family = poisson("log"), data = casos_ext)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -4.1378 -2.4478 -1.1613 0.9686 5.1583
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.558654 0.100183 5.576 2.46e-08 ***
## t 0.132376 0.003137 42.199 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 3047.68 on 37 degrees of freedom
## Residual deviance: 242.89 on 36 degrees of freedom
## AIC: 407.41
##
## Number of Fisher Scoring iterations: 5
## # A tibble: 2 x 4
## var Estimate ci_low ci_high
## <chr> <dbl> <dbl> <dbl>
## 1 (Intercept) 0.558 0.493 0.610
## 2 t 0.132 0.131 0.134
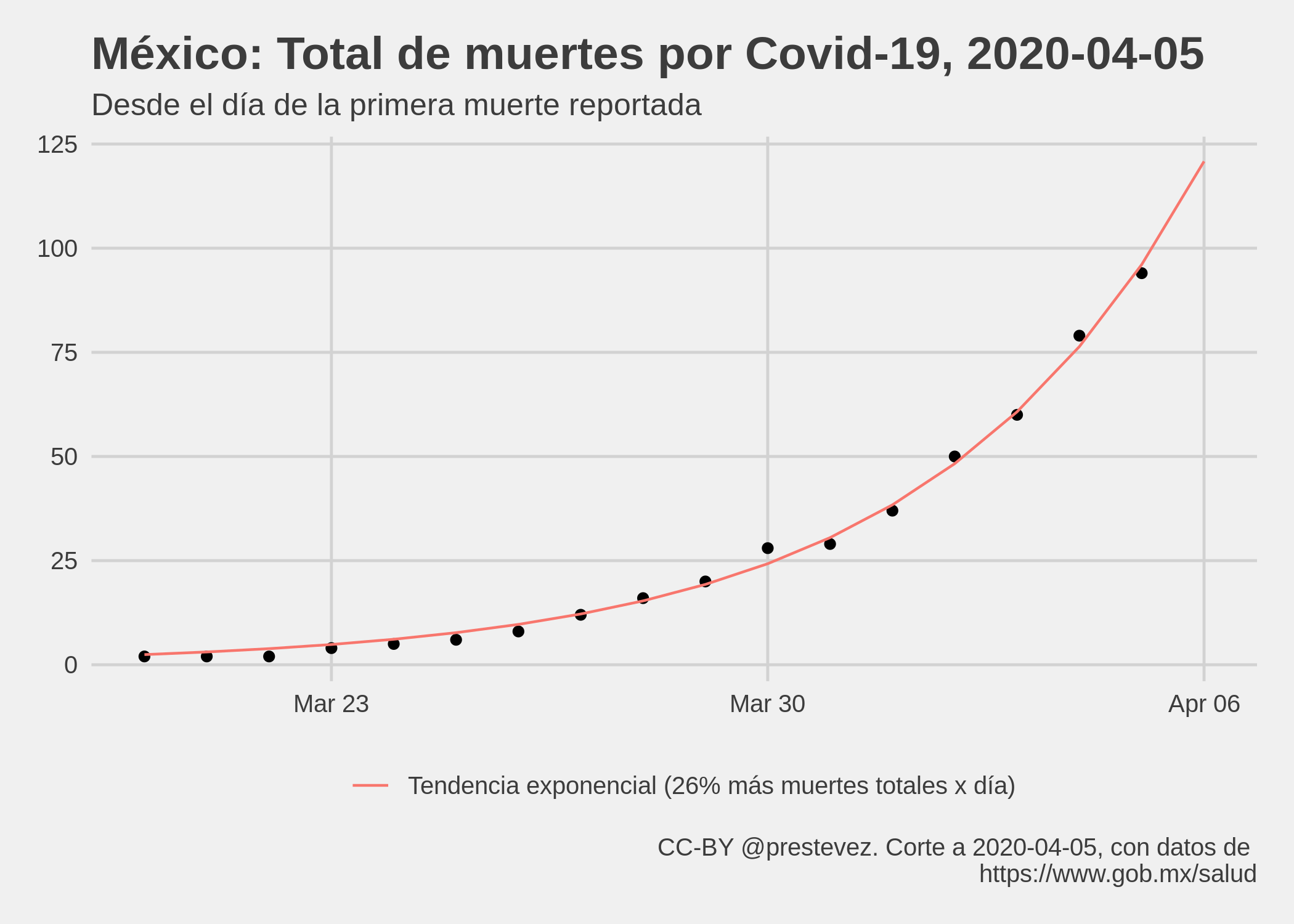
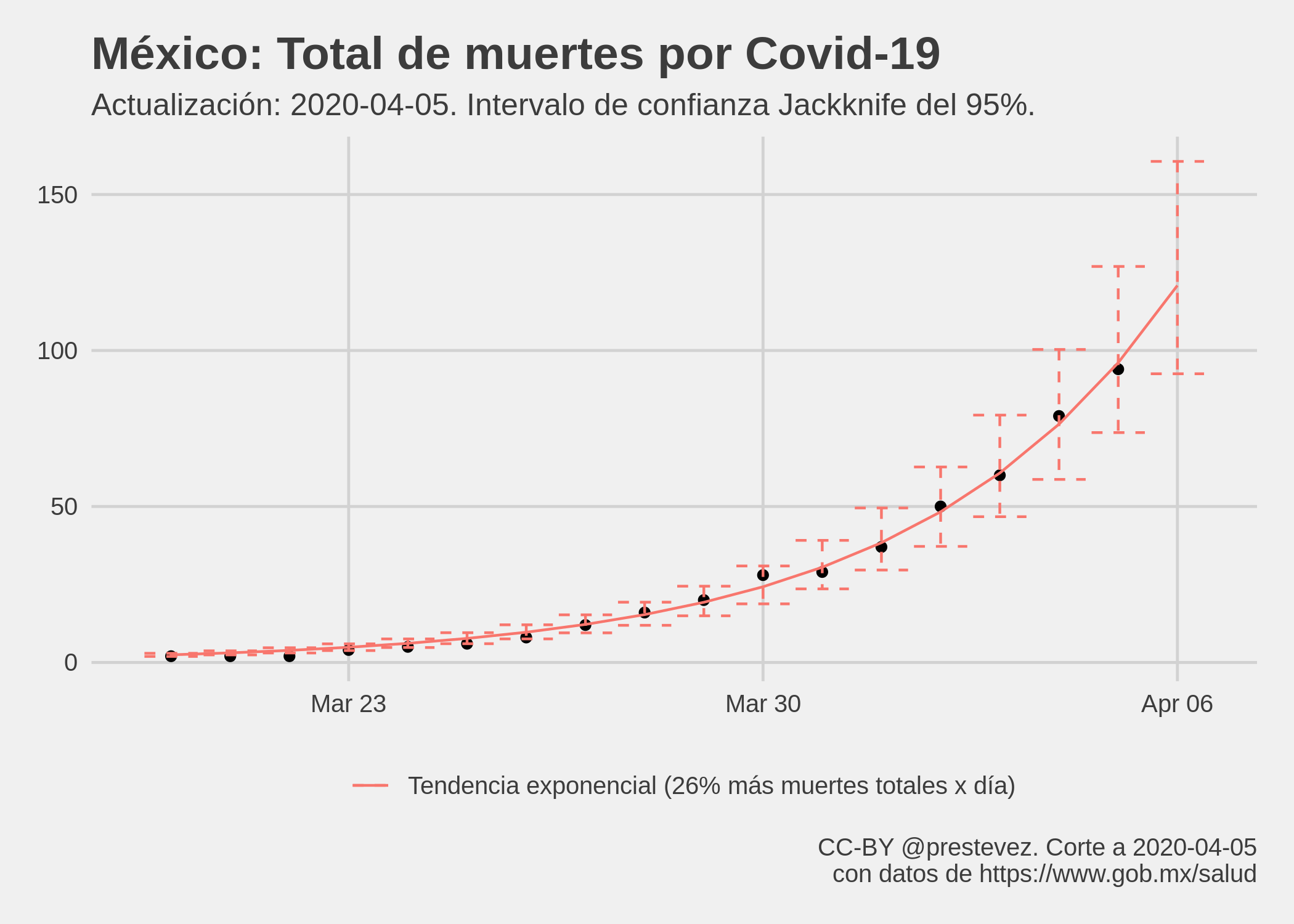
Utilizando la misma lógica que para el acumulado de casos, podemos modelar el acumulado de muertes y muertes nuevas para ver la tendencia de crecimiento en estas desde que se reportaron las primeras defunciones por covid-19. Cabe reiterar que estos modelos no son apropiados para capturar la dinámica real de las muertes causadas por la epidemia. Para ello se requieren modelos epidemiológicos. Estos modelos solo calculan las líneas de tendencia de las muertes totales y nuevas a la fecha, para estimar el ritmo de crecimiento. Se hacen extrapolaciones a un día para darse una idea de cuántas muertes totales y nuevas podrían verse mañana si las tendencias a la fecha se mantienen.
Mañana se espera que el total acumulado de casos confirmados de Covid-19 alcance 2565, con un intervalo de confianza Jackknife del 95% entre 2356 y 2794, si la tendencia observada hasta hoy se mantiene igual.
Según el modelo de casos nuevos, mañana se esperan 305 casos confirmados nuevos, con un intervalo de confianza Jackknife del 95% entre 269 y 348, si la tendencia observada hasta hoy se mantiene igual.
Según el modelo de muertes acumuladas, mañana se espera que el total alcance alrededor de 121 muertes, con un intervalo de confianza Jackknife del 95% entre 93 y 161, si la tendencia observada hasta hoy se mantiene igual.
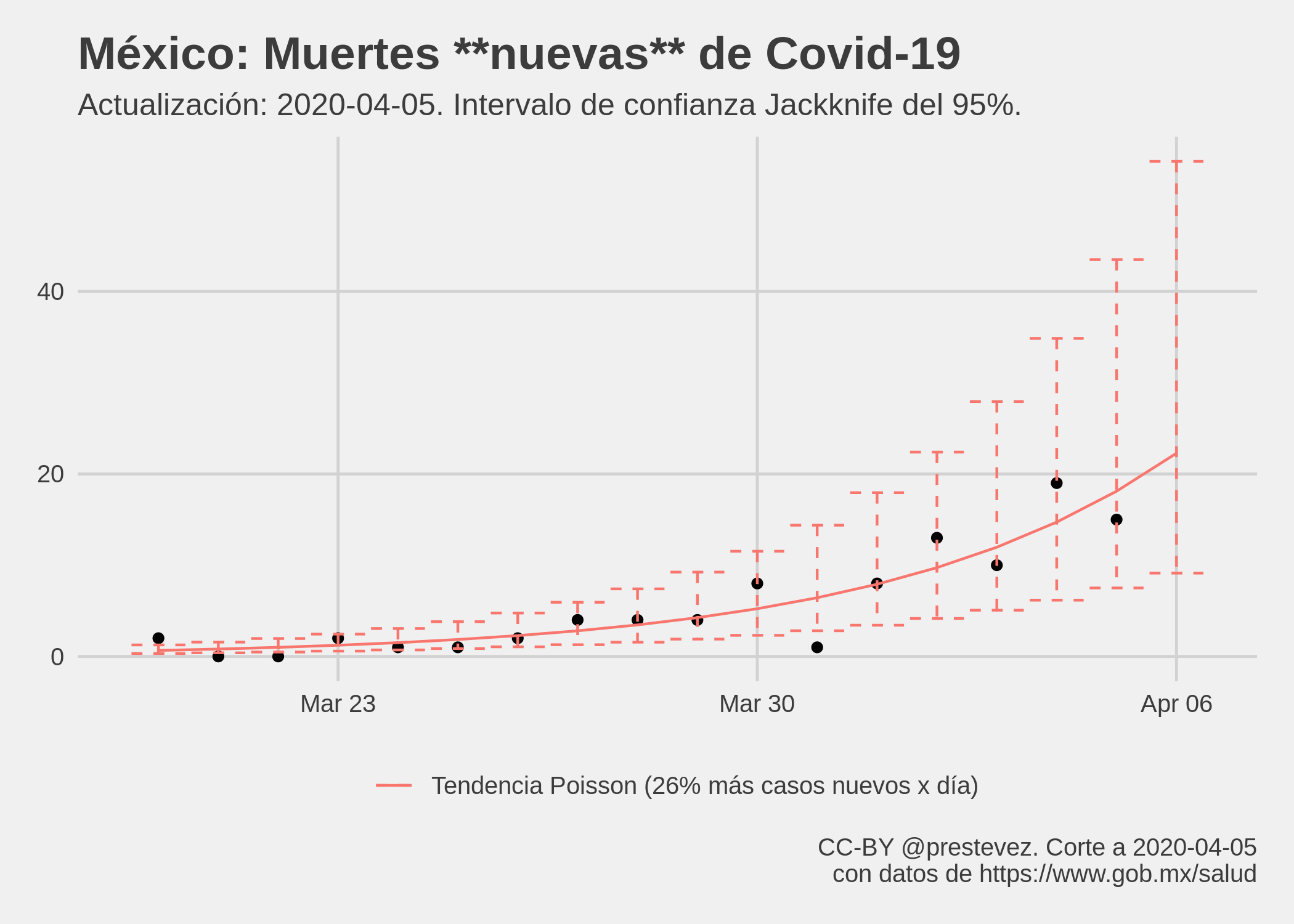
Según el modelo de muertes nuevas, mañana se esperan alrededor de 22 muertes nuevas, con un intervalo de confianza Jackknife del 95% entre 9 y 54, si la tendencia observada hasta hoy se mantiene igual.
Sin embargo, estas cifra muy probablemente estén equivocadas, pues los modelos usados son extremadamente simples. El objetivo es tener una vaga noción de las cifras esperadas.
Los modelos se actualizan cada día conforme se publican los datos de casos confirmados. En esta sección se presenta la diferencia entre el número de casos observados hoy contra el número de casos que se esperaban hoy según el modelo del día anterior.
Para el modelo del acumulado de casos:
| Fecha | Casos Totales Observados | Predicción | Error |
|---|---|---|---|
| 2020-03-15 | 53 | 51.89 | 1.11 |
| 2020-03-16 | 82 | 73.72 | 8.28 |
| 2020-03-17 | 93 | 115.68 | -22.68 |
| 2020-03-18 | 118 | 134.77 | -16.77 |
| 2020-03-19 | 164 | 163.96 | 0.04 |
| 2020-03-20 | 203 | 218.34 | -15.34 |
| 2020-03-21 | 251 | 273.56 | -22.56 |
| 2020-03-22 | 316 | 335.79 | -19.79 |
| 2020-03-23 | 367 | 415.43 | -48.43 |
| 2020-03-24 | 405 | 487.84 | -82.84 |
| 2020-03-25 | 476 | 545.18 | -69.18 |
| 2020-03-26 | 585 | 620.12 | -35.12 |
| 2020-03-27 | 717 | 730.57 | -13.57 |
| 2020-03-28 | 848 | 876.82 | -28.82 |
| 2020-03-29 | 993 | 1041.24 | -48.24 |
| 2020-03-30 | 1094 | 1222.78 | -128.78 |
| 2020-03-31 | 1215 | 1380.92 | -165.92 |
| 2020-04-01 | 1378 | 1537.02 | -159.02 |
| 2020-04-02 | 1510 | 1716.08 | -206.08 |
| 2020-04-03 | 1688 | 1890.01 | -202.01 |
| 2020-04-04 | 1890 | 2084.83 | -194.83 |
| 2020-04-05 | 2143 | 2304.40 | -161.40 |
Intervalos de confianza JK
| Fecha | Casos Totales Observados | Rango esperado | Fuera de rango |
|---|---|---|---|
| 2020-03-24 | 405 | 388-633 | No |
| 2020-03-25 | 476 | 423-732 | No |
| 2020-03-26 | 585 | 511-768 | No |
| 2020-03-27 | 717 | 636-846 | No |
| 2020-03-28 | 848 | 792-968 | No |
| 2020-03-29 | 993 | 936-1166 | No |
| 2020-03-30 | 1094 | 1106-1363 | Sí |
| 2020-03-31 | 1215 | 1230-1571 | Sí |
| 2020-04-01 | 1378 | 1383-1724 | Sí |
| 2020-04-02 | 1510 | 1558-1903 | Sí |
| 2020-04-03 | 1688 | 1707-2103 | Sí |
| 2020-04-04 | 1890 | 1892-2300 | Sí |
| 2020-04-05 | 2143 | 2100-2531 | No |
Para el modelo de casos nuevos:
| Fecha | Casos Nuevos Observados | Predicción | Error |
|---|---|---|---|
| 2020-03-22 | 65 | 70.92 | -5.92 |
| 2020-03-23 | 51 | 87.47 | -36.47 |
| 2020-03-24 | 38 | 91.69 | -53.69 |
| 2020-03-25 | 71 | 88.21 | -17.21 |
| 2020-03-26 | 109 | 99.55 | 9.45 |
| 2020-03-27 | 132 | 124.43 | 7.57 |
| 2020-03-28 | 131 | 154.15 | -23.15 |
| 2020-03-29 | 145 | 176.99 | -31.99 |
| 2020-03-30 | 101 | 200.17 | -99.17 |
| 2020-03-31 | 121 | 200.59 | -79.59 |
| 2020-04-01 | 163 | 207.60 | -44.60 |
| 2020-04-02 | 132 | 227.10 | -95.10 |
| 2020-04-03 | 178 | 232.28 | -54.28 |
| 2020-04-04 | 202 | 250.36 | -48.36 |
| 2020-04-05 | 253 | 272.22 | -19.22 |
Intervalos de confianza JK, casos nuevos.
| Fecha | Casos Nuevos Observados | Rango esperado | Fuera de rango |
|---|---|---|---|
| 2020-03-24 | 38 | 61-149 | Sí |
| 2020-03-25 | 71 | 58-144 | No |
| 2020-03-26 | 109 | 74-142 | No |
| 2020-03-27 | 132 | 97-165 | No |
| 2020-03-28 | 131 | 121-194 | No |
| 2020-03-29 | 145 | 141-225 | No |
| 2020-03-30 | 101 | 162-252 | Sí |
| 2020-03-31 | 121 | 157-265 | Sí |
| 2020-04-01 | 163 | 164-290 | Sí |
| 2020-04-02 | 132 | 188-291 | Sí |
| 2020-04-03 | 178 | 195-281 | Sí |
| 2020-04-04 | 202 | 209-318 | Sí |
| 2020-04-05 | 253 | 237-325 | No |
Para las muertes por covid-19:
| Fecha | Muertes Totales Observadas | Predicción | Error |
|---|---|---|---|
| 2020-04-01 | 37 | 40.87 | -3.87 |
| 2020-04-02 | 50 | 48.76 | 1.24 |
| 2020-04-03 | 60 | 62.98 | -2.98 |
| 2020-04-04 | 79 | 77.25 | 1.75 |
| 2020-04-05 | 94 | 99.24 | -5.24 |
Predcciones: acumulado de muertes por covid-19.
| Fecha | Muertes Totales Observadas | Rango esperado | Fuera de rango |
|---|---|---|---|
| 2020-04-01 | 37 | 13-138 | No |
| 2020-04-02 | 50 | 31-80 | No |
| 2020-04-03 | 60 | 47-83 | No |
| 2020-04-04 | 79 | 58-105 | No |
| 2020-04-05 | 94 | 78-126 | No |
Intervalos de confianza JK, acumulado de muertes.
Para las muertes nuevas por covid-19:
| Fecha | Muertes Nuevas Observadas | Predicción | Error |
|---|---|---|---|
| 2020-04-01 | 8 | 6.13 | 1.87 |
| 2020-04-02 | 13 | 8.30 | 4.70 |
| 2020-04-03 | 10 | 12.74 | -2.74 |
| 2020-04-04 | 19 | 14.23 | 4.77 |
| 2020-04-05 | 15 | 20.17 | -5.17 |
Predcciones: Muertes nuuevas por covid-19.
| Fecha | Muertes Nuevas Observadas | Rango esperado | Fuera de rango |
|---|---|---|---|
| 2020-04-01 | 8 | 0-229 | No |
| 2020-04-02 | 13 | 1-55 | No |
| 2020-04-03 | 10 | 2-68 | No |
| 2020-04-04 | 19 | 4-46 | No |
| 2020-04-05 | 15 | 7-57 | No |
Intervalos de confianza JK, muertes nuevas.
La tendencia exponencial del modelo sugiere que el número de casos confirmados se duplica cada 5.11 días. Este ritmo es más rápido que el observado a nivel global, pero es consistente con los ritmos de crecimiento observados durante las primeras semanas de la epidemia en otros países.
Cabe recalcar que el ritmo de aumento en los casos confirmados no es equivalente al ritmo de crecimiento de casos totales de Covid-19, pues como se mencionó, los casos confirmados dependen tanto del incremento en casos totales como de la cantidad de pruebas realizadas. Es probable que conforme aumente la cantidad de pruebas realizadas, el ritmo de crecimiento de los casos confirmados se haga más lento.
De la misma forma, los modelos y predicciones de muertes relacionadas a covid-19 sufren también de errores de medición: es posible que los datos reportados no logren capturar el total de muertes por covid-19. Por tanto las tendencias no representan el fenómeno real.
Los modelos presentados no consideran el efecto que puedan tener las medidas de mitigación de la epidemia en la cantidad de casos confirmados o muertes en el futuro. Como se ha mostrado en la evidencia académica, y se ilustra magistralmente en el artículo de Harry Stevens en el Washington Post, las medidas de contención y mitigación como aislamiento de pacientes, cuarentenas a ciudades y regiones, y especialmente el distanciamiento social, han demostrado ser efectivas para alentar el ritmo de crecimiento de la epidemia.
En la medida que dichas medidas se adopten con vigor en México, se esperaría que el crecimiento de casos confirmados de Covid-19 en el país sea más lento.
Los modelo presentados son modelos estadísticos básicos que no consideran supuestos epidemiológicos o médicos relevantes para predecir con mayor precisión cómo evolucionará la epidemia de Covid-19 en el país. La información es de carácter informativo solamente.
Modelar epidemias de forma precisa es complejo y difícil, aun más en el caso de una enfermedad nueva como la Covid-19. Por tanto, reitero que mi objetivo no es modelar cuál va a ser el comportamiento de largo alcance de la epidemia.
Mi objetivo es mucho más modesto: solo se busca dar una idea general de cuántos casos confirmados o muertes de Covid-19 podrían reportarse mañana según la tendencia observada hasta el presente, reconociendo que dicha predicción está sujeta a errores de medición y modelado.
Para reproducir este análisis usando R, clona o descarga el repositorio y corre:
# requiere {rmarkdown}, {tidyverse} y {ggthemes}
rmarkdown::render("README.Rmd")- 19-03-2020: La extrapolación se redujo a 1 día dados los errores de predicción del modelo. Se expandió la sección de aclaración. Se corrigió el cálculo del tiempo en el que se espera que se dupliquen el total de casos confirmados. El cálculo anterior estaba sesgado hacia abajo (el tiempo calculado era menor, el cálculo anterior era 2/exp(Beta) = t, debe ser log(2)/Beta = t).
- 23-03-2020: Se agregó un modelo Poisson de casos nuevos. Se agregaron Jackknife estimates.
- 03-04-2020: Se agregaron gráficas y predicciones para muertes totales y nuevas.
- 05-04-2020: Se dejó de actualizar el proyecto.
Esta
obra está bajo una
Licencia
Creative Commons Atribución 4.0 Internacional.