All the quantum algorithms at one place.
This project is aimed on collecting quantum computing algorithms. Inviting contributions from all quantum developers worldwide. You can make contributions in any quantum framework you like wether it be Qiskit or Q# or any other. Follow the below instructions to make a contribution to this project.
- Fork this repository.
- Add your code into the folder with name of you framework used. If you do not see any such folder feel free to create one and edit this readme below by adding the name of your framework used and write a description about it.
- Make a pull request. We will accept your contribution if it is valid and verified.
- Since it is the beginning phase, if you want to change the folder structure then feel free to raise an issue.
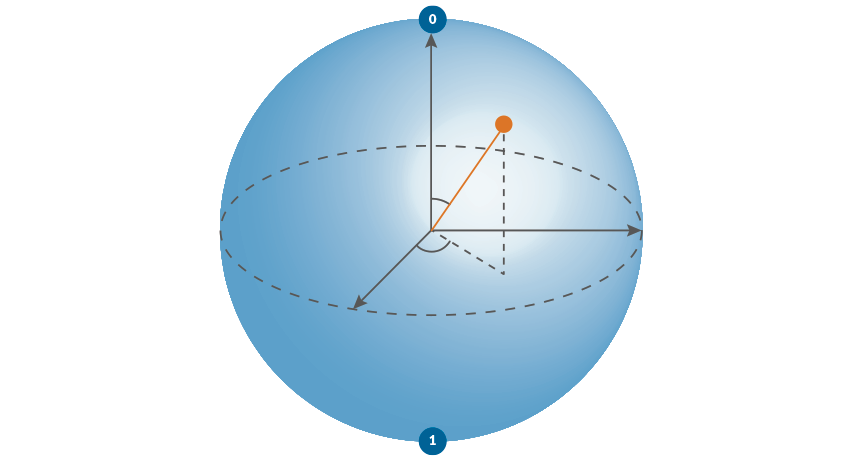
Quantum computing is the use of quantum phenomena such as superposition and entanglement to perform computation. Computers that perform quantum computations are known as quantum computers. Quantum computers are believed to be able to solve certain computational problems, such as integer factorization (which underlies RSA encryption), substantially faster than classical computers.
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical (or non-quantum) algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a problem, where each step or instruction can be performed on a classical computer. Similarly, a quantum algorithm is a step-by-step procedure, where each of the steps can be performed on a quantum computer. Although all classical algorithms can also be performed on a quantum computer,the term quantum algorithm is usually used for those algorithms which seem inherently quantum, or use some essential feature of quantum computation such as quantum superposition or quantum entanglement.