probirghosh45/DSA-learning

It is a document repository. I'm learning DSA so I created this repository to note down all the things, that might benefit many others. In this repository, I have tried to cover all the important topics of data structures and algorithms.

Welcome To DSA Learning

Here is the all chapter that we will learn in this docs

• Big O Notation
• Recursion
• Linear Search
• Binary Search
• Bubble Sort
• Selection Sort
• Insertion Sort
• Stack
• Queue
• Linked List
• Binary Tree

Algorithms

Big O Notation

> Big-O notation হচ্ছে আমাদের কোনো একটা function এর ইনপুট বাড়ার সাথে সাথে কতটা টাইম কমপ্লেক্সিটি ও কতটা স্পেস কমপ্লেক্সিটি হচ্ছে সেটা নির্ণয় করা। এটি একটি টুল যার সাহায্যে কোনো একটা অ্যালগরিদমের রানটাইমের উপর ভিত্তি করে টাইম কমপ্লেক্সিটি বের করা যায়। Big O notation কোনো অ্যালগরিদমের টাইম কমপ্লেক্সিটি ও কতটা স্পেস কমপ্লেক্সিটি নির্ণয় করতে ব্যবহৃত হয়, তাদের মধ্যে বৃদ্ধির হার হিসেবে প্রকাশিত হয়। উদাহরণস্বরূপ, O(1), O(log n), O(n), O(n log n), O(n^2) ইত্যাদি।

Big-O notation এর মাধ্যমে আমাদের প্রতিনিয়ত ব্যবহৃত কয়েকটা জাভাস্কিপ্ট মেথত এর টাইম কমপ্লেসিটি ও স্পেস কমপ্লেসিটি নির্ণয় করি

=> Big O(n) - যখন কোনো ইনপুট আমাদের অনিশ্চিত থাকে ( মানে কতগুলো ইনপুট অথবা ভেলু থাকতে পারে অথবা আউটপুট আসতে পারে আমরা জানি না ) তখন আমরা সেটাকে n হিসেবে নেই, এবং যে সকল মেথডের টাইম কমপ্লেক্সিটি আমরা নির্ণয় করার সময় এইরকম ভাবে অনিশ্চিত ইনপুট আসতে পারে পাই সেগুলোকে আমরা Big O(n) বলি।

=> Big O(1) - যখন কোনো ইনপুট আমাদের নিশ্চিত থাকে ( মানে আমরা জানি যে ওইটা শুধুমাত্র একটা আউটপুট দিবে আমাদের কন্ডিশন অনুযায়ী ) তখন আমরা সেটাকে 1 ধরি, এবং যে সকল মেথডের টাইম কমপ্লেক্সিটি আমরা নির্ণয় করার সময় এইরকম ভাবে নিশ্চিত ইনপুট আসতে পারে পাই সেগুলোকে আমরা Big O(1) বলি।

Object

• Object.keys - Big O(n)

  ( এটায় Big O(n) কারণ একটি object এ অনেক keys তাকতে পারে এটা বলা মুশকিল যে ওই object এর মধ্যে মোট কতটি entries তাকবে, তাই আমরা ধরে নিলাম যে একটা n ইনপুটে থাকবে এবং সেই n এ যত ইচ্ছা দেওয়া হবে তাই এটা n এর উপর ডিপেন্ডেড এবং এর জন্যই এটা Big O(n) )

• Object.entries - Big O(n)

  ( same as object.keys )

• Object.values - Big O(n)

  ( same as object.keys )

• Object.hasOwnProperty - Big O(1)

  ( এটায় Big O(1) কারণ আমরা যখন কোনো property সার্চ করবো তখন তো আমরা একটা value ই পাবো এবং এর জন্যই এটা Big O(1) )

Array

• push, pop - Big O(1)

  ( এটায় Big O(1) কারণ একটি array তে আমরা যখন push or pop এর মাধ্যমে কোনো element যুক্ত করি তখন সেই element টি ওই array এর শেষের দিকে যুক্ত হয় অথবা ডিলিট হয়, যার জন্য কোনো element এর ইনডেক্স পরিবর্তন করতে হয় না এবং এর জন্যই এটা Big O(1) )

• shift, unshift - Big O(n)

  ( এটায় Big O(n) কারণ একটি array তে আমরা যখন shift or unshift এর মাধ্যমে কোনো element যুক্ত করি তখন সেই element টি ওই array এর শুরুর দিকে যুক্ত হয় অথবা ডিলিট হয়, যার জন্য আগের element দের ইনডেক্স পরিবর্তন করতে হয়। তাই এখানে n বার নতুন element যুক্ত হতে পারে যার জন্যই এটা Big O(n) )

• search - Big O(n)

  ( এটায় Big O(n) কারণ একটি array তে কতগুলো value তাকবে তা বলা যাবে না এবং আমরা যদি ওই array তে কোনো কিছু search করি তাহলে আমাদের ওই array তে থাকা প্রতিটি element এর মধ্যে দিয়ে খুজতে হবে আমাদের কাংকিত element টিকে এবং সেটা n তম বার ও হতে পারে যার জন্যই এটা Big O(n) )

• access - Big O(1)

  ( এটায় Big O(1) কারণ একটি array থেকে আমরা যখন কোনো একটা element access করতে চাই তার index এর মাধ্যমে তখন কিন্তু আমরা সরাসরি ওই element টাকে access করতে পারি এবং সেটা একটি element হয় যার জন্যই এটা Big O(1) )

• forEach - Big O(n)

  ( এটায় Big O(n) কারণ একটি forEach এ কতগুলো ইনপুট আসবে সেটা আমরা জানি না। এখন সেটা অনেক বড় কোনো ইনপুট হতে পারে আবার ছোটও হতে পারে তার জন্যই এটা Big O(n) )

• map - Big O(n)

  ( এটায় Big O(n) কারণ একটি map এ কতগুলো ইনপুট আসবে সেটা আমরা জানি না। এখন সেটা অনেক বড় কোনো ইনপুট হতে পারে আবার ছোটও হতে পারে তার জন্যই এটা Big O(n) )

• filter - Big O(n)

  ( এটায় Big O(n) কারণ একটি filter এ কতগুলো ইনপুট আসবে সেটা আমরা জানি না। এখন সেটা অনেক বড় কোনো ইনপুট হতে পারে আবার ছোটও হতে পারে তার জন্যই এটা Big O(n) )

• reduce - Big O(n)

  ( এটায় Big O(n) কারণ একটি reduce এ কতগুলো ইনপুট আসবে সেটা আমরা জানি না। এখন সেটা অনেক বড় কোনো ইনপুট হতে পারে আবার ছোটও হতে পারে তার জন্যই এটা Big O(n) )

Recursion

> Recursion বিষয়টি হচ্ছে কোনো একটা প্রবলেমকে ভেঙ্গে ভেঙ্গে করাকে বুঝায়। Recursion এর মাধ্যমে আমরা কোনো একটা প্রবলেম normal way তে যেভাবে করে যেমন output পাই ঠিক তেমনি output পাবো Recursion way তে করার মাধ্যমে শুধু পরিবর্তনটি হবে আমরা যখন Recursion way তে কোড করবো তখন আমরা ধাপে ধাপে একটা প্রবলেম সল্ভ করবো।

Searching Algorithms

Linear Search

> Lineasr Search বিষয়টি হচ্ছে কোনো একটা স্পেসিফিক জায়গা থেকে কোনো একটা জিনিস খুজে দিবে এবং খুজে দেয়ার পর সেখান থেকে চলে আসবে। তার মানে হচ্ছে আমরা বলে দিবো যে এই জায়গা থেকে আমাকে তুমি এই জিনিসটা এনে দাও linear search বিষয়টি হচ্ছে এইরকম।

Binary Search

> binary search আমাদের টাইম কমপ্লেক্সিটি অনেক কমিয়ে দেয় এবং আমরা যে এলিমেন্ট খুজতে চাচ্ছি সেটা খুব সহজে বের করতে পারি। binary search করতে হলে আমাদের আগে আমাদের যে array টি থাকবে সেটাকে ascending order এ সাজাতে হবে এবং পরে সেটার উপর সার্চ করতে পারবো।

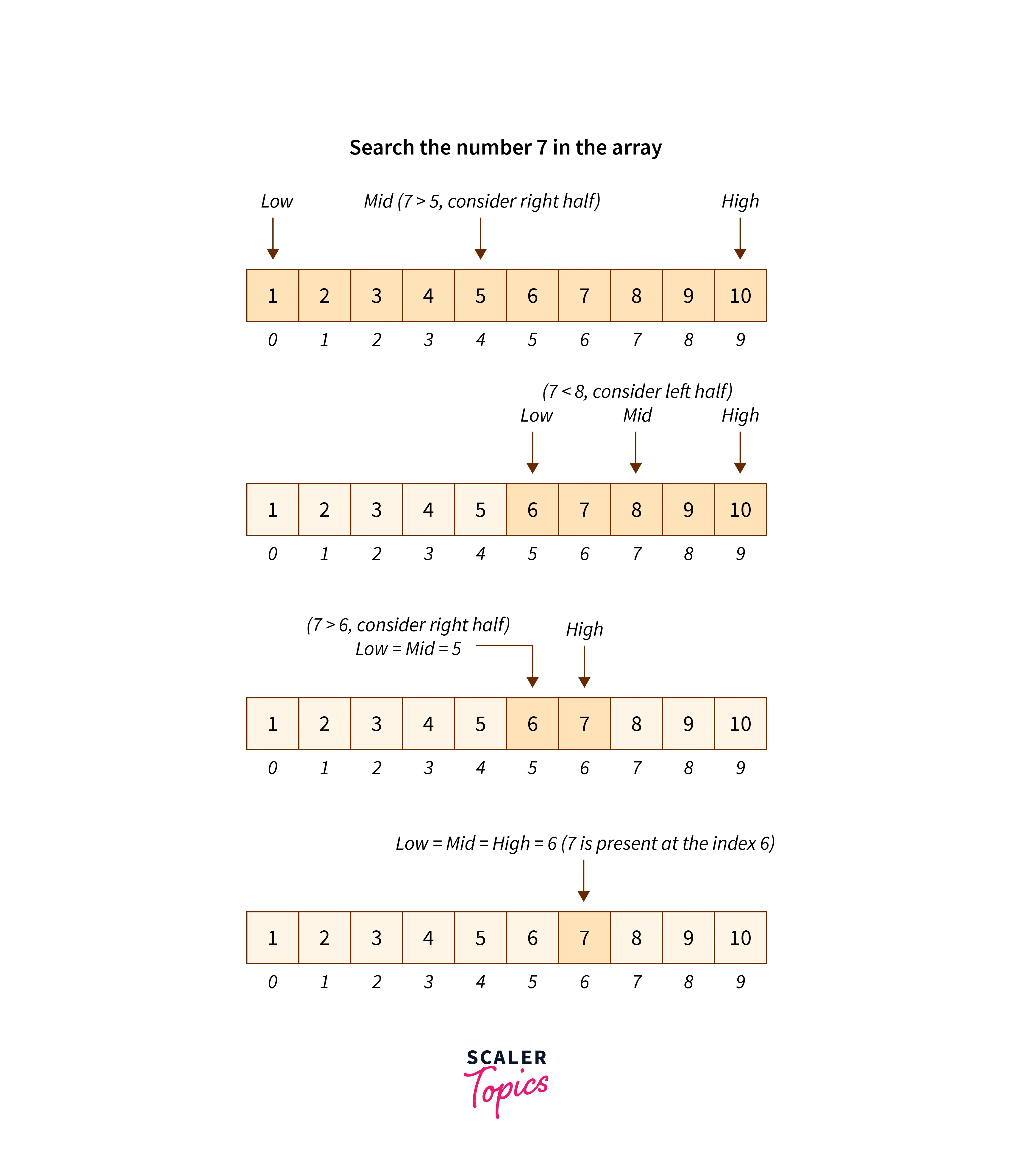
তাহলে চলেন নিচের ইমেজের মাধ্যমে আরো ভালোভাবে বুঝার চেষ্টা করি।

binary search এ আমরা তিনটি পয়েন্ট করি প্রথমে এবং সেই পয়েন্ট অনুসারে আমাদের যেই এলিমেন্ট খুজছি সেটা পাবো।

পয়েন্ট গুলো হচ্ছে,

1. Start Point
2. Middle Point
3. End Point

উপরের তিনটি পয়েন্টের মাধ্যমে আমরা খুব কম সময়ের মধ্যে আমদের যেই এলিমেন্ট খুজছি সেটা খুজে পাবো।

এখানে প্রসেসটি হচ্ছে এইরকম, আমরা প্রথমে সিলেক্ট করবো যে আমাদের start point কোনটি তারপর সিলেক্ট করবো আমাদের middle point কোনটি এবং শেষে সিলেক্ট করবো আমাদের end point কোনটি। এইগুলো সিলেক্ট হয়ে গেলে আমরা কন্ডিশন এর মাধ্যমে খুজে দেখবো যে আমাদের কাংক্ষিত এলিমেন্ট কি middle এর চেয়ে বড় নাকি ছোট ? যদি বড় হয় তাহলে আমরা সেই middle এলিমেন্ট এর পরের সব এলিমেন্ট বাদ দিয়ে দিবো কারণ আমাদের array টি তো ascending order এ সাজানো তাই না ? এবং যেহেতু আমাদের কাংক্ষিত এলিমেন্টটি middle এলিমেন্ট এর চেয়ে ছোট তাই আমরা middle এর আগের সব এলিমেন্ট এর উপর এখন search চালাবো এবং আমরা আমাদের start, middle, end point গুলো পরিবর্তন করে ফেলবো এভাবে যে আমাদের আগের middle point যেটা ছিলো সেটা হবে এখন end point এবং যেহেতু আমরা শেষের গুলো বাদ দিয়ে প্রথম দিকের এলিমেন্ট গুলোর উপর search করছি তাই আমদের আর start point পরিবর্তন করতে হবে না তাই middle point and end point পরিবর্তন করবো। এবং ওইখানে দেখবো যে এখন যেটা middle এলিমেন্ট আছে সেটা কি আমাদের কাংক্ষিত এলিমেন্ট এর চেয়ে ছোট নাকি বড় ছোট হলে তো আগের মতই পরিবর্তন করবো আর বড় হলে ও এবং যদি মিলে যায় তাহলে তো আমাদের output পেয়ে যাচ্ছি ( so now you can chill মজা করলাম )।

মুলত এইভাবেই binary search করা হয়। আর picture তো যুক্ত করে দিলামই যাতে আপনারা নিজে আর ভালো বুঝতে পারেন আমার বুঝানোর চেয়ে।

Sorting Algorithms

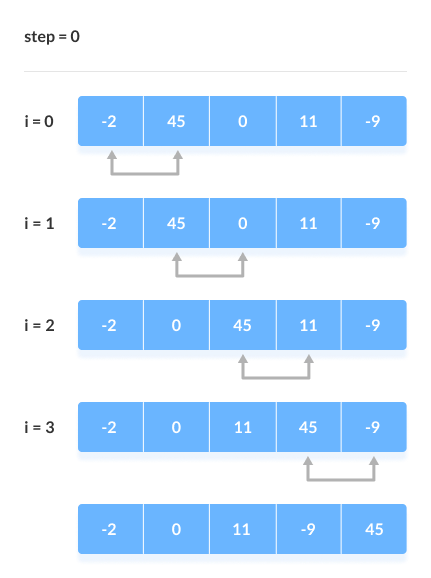
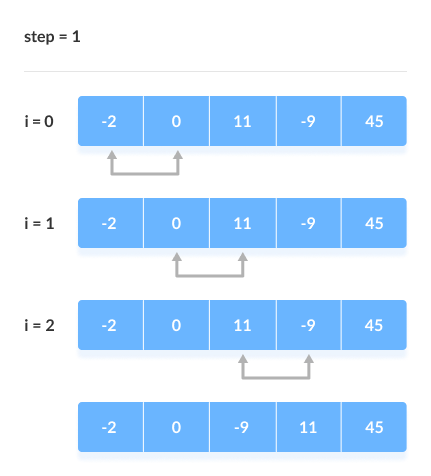
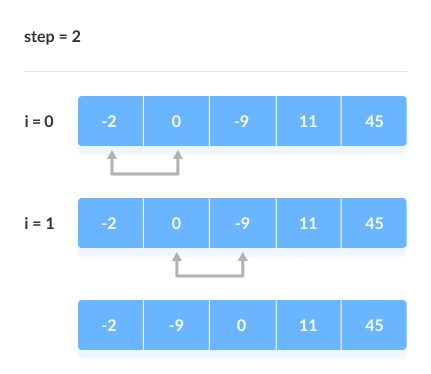
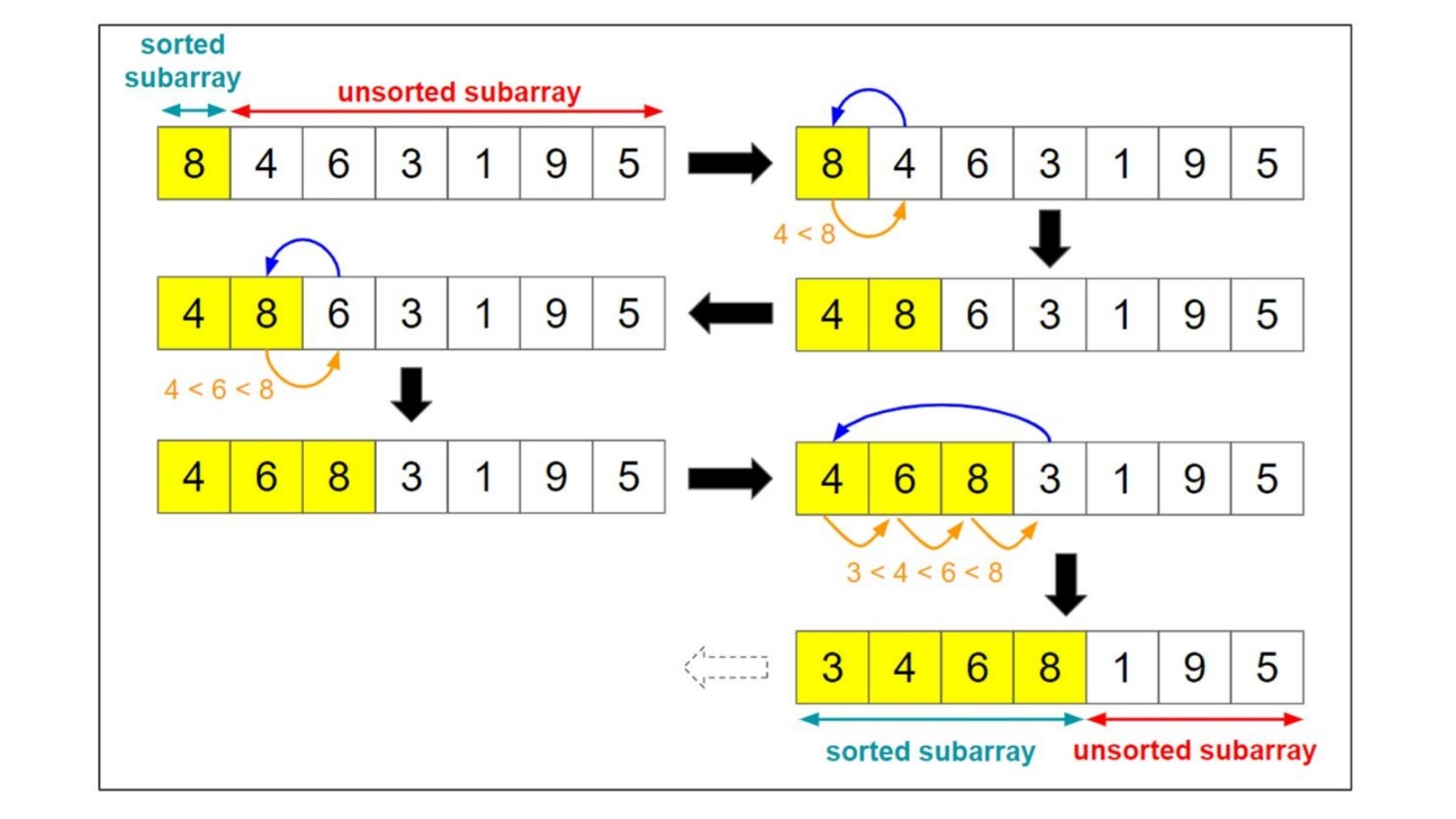
> sorting slgorithms হচ্ছে কোনো একটা array কে ascending order এ কিংবা descending order এ সাজানোর জন্য ( ছোট থেকে বড় কিংবা বড় থেকে ছোট )। আমরা এই sorting algorithms এর মধ্যে অনেকগুলো algorithms পাই জেগুলো ব্যবহার করে খুব সহজে যেকোনো array sort করতে পারবো। নিচে কিছু দেয়া হলো,

Bubble Sort

> bubble sort এর মাধ্যমে আমরা একটি array এর ২টি value নিয়ে নিয়ে তাদের মধ্যে compare করে দেখবো যে প্রথম value এর চেয়ে দ্বিতীয় value বড় নাকি ছোট যদি বড় হয় তাহলে আমরা swape করবো value গুলোকে, যেমন আমাদের প্রথম value বড় হলো দ্বিতীয় value এর চেয়ে তাহলে তো আমরা বুঝতে পারছি যে আমাদের ডান পাশের value টি হচ্ছে ছোট value এবং তাকে বাম পাশে আনতে হবে এবং বাম পাশের value কে ডান পাশে দিতে হবে। এভাবেই চেক করে করে আমরা bubble sorting করবো। এবং আরেকটা কথা হচ্ছে আমরা যখন সর্বশেষ লাস্ট বড় এলিমেন্ট পেয়ে যাব তখন দ্বিতীয় বার আর ওই লাস্ট এলিমেন্টকে বাম পাশের এলিমেন্ট দ্বারা চেক করবো না এবং এভাবেই চেকিং হবে।

নিচে কয়েকটি স্টেপের মাধ্যমে আর ক্লিয়ার করার চেষ্টা করেছি

আমি একটা ওয়েবসাইটের লিংক দিচ্ছি যেটাতে গেলে আপনি একটি ভিডিওর মাধ্যমে আরো ভাবে বুঝতে পারবেন যে operation টি হচ্ছে কেমনে।

https://visualgo.net/en/sorting

Selection Sort

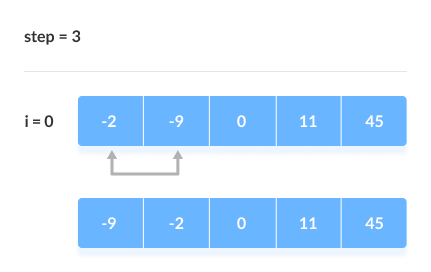
> Selection Sort বিষয়টি হচ্ছে একদম bubble sort এর মতই শুধু পরিবর্তনটি হচ্ছে আমরা bubble sorting এ তিনটি পয়েন্ট ধরতাম এবং সেগুলো দিয়ে array টি sort করতাম, কিন্তু selection sorting এ আমরা শুধুমাত্র একটি পয়েন্ট ধরবো যেটা হচ্ছে একটা lowest number এবং আমরা চেক করবো যে আমাদের lowest number কি তার পাশের number এর চেয়ে বড় ? যদি বড় হয় তাহলে তো আমাদের পাশের number টিকে lowest number এর ইনডেক্সে আনতে হবে কেননা ওই পাশের number টাই তো ছোট number এবং সেটা lowest number এর জায়গায় আসলে তবেই তো sorting টি হবে ছোট থেকে বড় হয়ে। এবং সংখ্যাটিকে আনার জন্য তো আমাদের swape করতে হবে তাই না ? আমরা swape করবো টিক যেভাবে bubble sort এ swape করেছিলাম ঠিক ওইভাবে।

আপনাদের বুঝার জন্য নিচে picture যুক্ত করেছি এবং একটি video ও যুক্ত করে দিয়েছি যাতে আপানারা খুব সহজে বিষয়টি বুঝতে পারেন।

video link - https://visualgo.net/en/sorting

Insertion Sort

> Insertion Sort ঠিক selection sort এর মতই কিন্তু এখানে পরিবর্তনটি হচ্ছে, আমরা selection sorting এ বাম পাশের number এর সাথে ডান পাশের number এর ছোট এবং বড় কি না সেটা চেক করতাম। কিন্তু insertion sorting এ আমরা একই ভাবে ডান পাশের টার সাথে ছোট বড় চেক করবো কিন্তু যদি ডান পাশের number টি বাম পাশের number এত ছোট হয় যে সেটাকে আমার আর ২ ইনডেক্স সামনে আনার প্রয়োজন হচ্ছে তখন insertion sort এ backword cheking করা হয় এবং ওই number এর সঠিক পজিশনে পৌঁচে দেওয়া হয়। এবং insetion sorting এ আমরা এইভাবে চেকিং করতে করতে সামনের দিকে এগুতে থাকি আর এইরকম পরিস্তিতির সম্মুখীন হলে backword checking এর মাধ্যমে ওই number টির সঠিক পজিশনে নেয়া হয়।

আপনাদের বুঝার জন্য নিচে picture যুক্ত করেছি এবং একটি video ও যুক্ত করে দিয়েছি যাতে আপানারা খুব সহজে বিষয়টি বুঝতে পারেন।

video link - https://visualgo.net/en/sorting

Data Structure

> Data Structure হচ্ছে একটি ওয়েবসাইটে আমাদের যত প্রয়োজনীয় ডাটা আছে সেগুলোকে খুব সুন্দর ভাবে সাজিয়ে রাখার মাধ্যম। ডাটা গুলো সুন্দর করে সাজিয়ে রাখলে পরবর্তীতে যখন আমি ওই ডাটাটি খুজতে যাবো অথবা ডাটাটি আপডেট করতে যাবো তখন আমার অন্য কোথাও খুজতে হবে না কারণ আমি জানি যে আমি এই ফাইলের মধ্যে ডাটাটি রেখেছি এবং তখন সরাসরি ওই ফাইলে যাবো এবং ডাটাটি নিয়ে আসতে পারবো। আর এটাই হচ্ছে data structure.

Stack

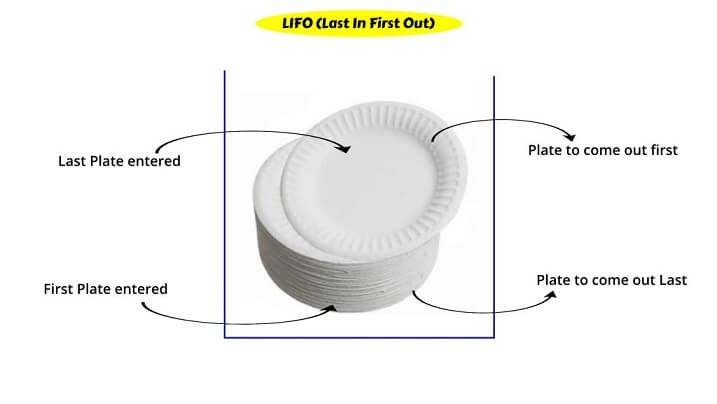
> stack এর একটি প্রিন্সিপাল রয়েছে এবং সেটা হচ্ছে (LIFO).

• L = Last
• I = In
• F = First
• O = Out

এক কথায়, Last In First Out বলা হয়েছে এখানে। যেটার মানে হচ্ছে যে সবার শেষে আসবে সে সবার প্রথমে বেরিয়ে যাবে এবং যে সবার প্রথমে আসবে সে সবার শেষে বেরিয়ে যাবে।

ওকে, জিনিসটা আর ক্লিয়ার করি একটি ইমেজের মাধ্যমে.........

এখানে ইমেজটি লক্ষ করুন, আমি যখন প্লেট রাখছিলাম তখন একটার উপর একটা এভাবে রাখছিলাম এবং আমি সব প্লেট রেখে দিয়েছি। পরে আমার আম্মু বললো যে উনাকে একটা প্লেট এনে দিতে, তো আমি গিয়ে উপরে যে প্লেটটি আছে সেটি নিয়ে এসে উনাকে দিবো তাই না ? হে, কারণ আমি চাইবো না যে নিচ থেকে একটা প্লেট এনে দেই কারণ সে ক্ষেত্রে পুরো প্লেটের স্তুবটি ভেঙ্গে যেতে পারে এবং না ভাঙ্গলে ও এতো কষ্ট নিয়ে আসবো না আমি। তাহলে এখানে ঘটনা কি হলো ? আমি যেই প্লেটটি সবার প্রথমে রেখেছিলাম সেটা নিচে রয়ে গেলো এবং যেই প্লেটটি সবার শেষে রেখেছিলাম সেটা উপরে রয়ে গেলো এবং আমি যখন প্লেট নিতে আসছি তখন ওই উপরের প্লেটটি নিয়ে গেছি। তাহলে আমাদের LIFO এর প্রমাণ হয়ে গেলো।

Queue

> Queue এর একটি প্রিন্সিপাল রয়েছে এবং সেটা হচ্ছে (FIFO).

• F = First
• I = In
• F = First
• O = Out

এক কথায়, First In First Out বলা হয়েছে এখানে। যেটার মানে হচ্ছে যে প্রথমে আসবে সে প্রথমে বেরিয়ে যাবে এবং যে শেষে আসবে সে শেষে বেরিয়ে যাবে।

এখানে ইমেজটি লক্ষ করুন, ইমেজে ২টি পার্ট রয়েছে একটা হচ্ছে front এবং আরেকটা হচ্ছে back. তো আমরা যে ডাটা গুলো insert(যুক্ত করবো) সেগুলো back পার্ট দিয়ে যুক্ত হবে এবং যখন আমরা সেই ডাটাটি get(পেতে চাইবো) তখন front পার্ট দিয়ে বেরিয়ে আসবে। এবং অবশ্যই সেক্ষেত্রে আমরা সে ডাটা আগে যুক্ত করবো সেটা আগে বেরিয়ে আসবে এবং সেটা পরে যুক্ত করবো সেটা পরে বেরিয়ে আসবে। তাহলে আমাদের FIFO এর প্রমাণ হয়ে গেলো।

Linked List

> Linked List যেহেতু অনেক বড় একটি টপিক তাই আমি এই টপিক এর জন্য আলাদাভাবে আরেকটি রিপোজিটরি তৈরি করেছি এবং সেখানে Linked List নিয়ে খুব ভালোভাবে আলোচনা করার চেষ্টা করেছি এবং নিচে সেই রিপোজিটরির লিংক দিয়েছি,

Repository Link - https://github.com/Asfak00/linked-list-full-explained

Binary Tree

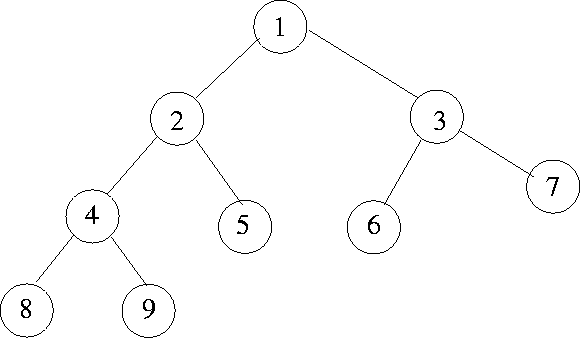
> যে ট্রি এর নোডগুলোতে সর্বোচ্চ দুইটি child থাক্কে পার তাকে বাইনারি ট্রি বলা হয়। নোডগুলোতে লিঙ্কড লিস্টের মোট এর বা একাধিক ডেটা স্টোর করার ফিল্ড/ভেরিয়েবল থাকতে পারে। আর থাকবে এই নোডের left child এবং right child এর মেমরি এড্রেস। যার মাধ্যমে এদেরকে অ্যাক্সেস করা যায়।

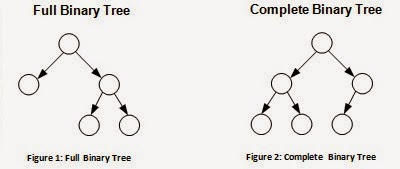
Binary Tree হচ্ছে ৩ প্রকারঃ

1. Full Binary Tree
2. Complete Binary Tree
3. Perfect Binary Tree

Full Binary Tree

> এমন একটা বাইনারি ট্রি যার নোডগুলোতে ০ থেকে ২ টি child থাকতে পারে। অর্থাৎ কোনও নোডে একটা child থাকলে সেটা full binary tree হবে না। একে proper binary tree, strictly binary tree বা plane binary tree বলা হয়।

Complete Binary Tree

> যে বাইনারি ট্রি এর শেষ লেভেল বাদে বাকি সব লেভেল সম্পূর্ণ ভাবে child দ্বারা পূর্ণ তাকে Complete Binary Tree বলে। অর্থাৎ সবগুলো নোডেই দুটি করে child আছে এবং শেষের লেভেলের ক্ষেত্রে নোডগুলো fill up হতে হবে একদম বাম বাশ থেকে। বামের দিকের কোনো একটা নোডের জায়গা ফাঁকা রেখে ডান দিকে নোড যুক্ত করলে তাকে Complete Binary Tree বলা যাবে না।

Perfect Binary Tree

> যেই বাইনারি ট্রি এর প্রত্যেকটি inteior node দুটি child থাকে এবং সকল leaf এর depth ও level একই হবে।

Binary Search Tree - Add Node

> আমরা জানি যে আমাদের binary tree তে একটি root রয়েছে। এবং সেই root এর under এ left এবং right রয়েছে। আর binary tree এর left এ থাকা সব node কিন্তু ছোট হয়ে থাকে এবং right এ থাকা সব node বড় হয়ে থাকে। তাই আমরা যে নতুন node যুক্ত করতে চাচ্ছি যেটা বড় হলে right এ পাঠিয়ে দিবো আর ছোট হলে left এ পাঠিয়ে দিবো। এখন প্রথমে আমাদের চেক করতে হবে যে আমাদের tree তে আধো কোনো root আছে কি না কারণ শুরুর দিকে তো আমাদের কোনো root থাকবে না তাহলে আমাদের প্রথমে root তৈরি করতে হবে। এবং সেজন্যই আমরা চেক করবো যে আমাদের কোনো root আছে কি না যদি না থাকে তাহলে আমরা যে নতুন node যুক্ত করতে চাচ্ছি সেটাকে বানিয়ে দিবো root। আর যদি আমাদের tree তে root থেকে থাকে তাহলে আমরা চেক করবো যে আমরা যে নতুন node যুক্ত করতে চাচ্ছি সেটি কি আমাদের root এর চেয়ে বড় নাকি ছোট। যদি ছোট হয় তাহলে নতুন node কে পাঠিয়ে দিবো left এর দিকে আর যদি বড় হয় তাহলে নতুন node কে পাঠিয়ে দিবো right এর দিকে। এখন যখন নতুন node left অথবা right এ যাবে তখন ওইখানে ও তো left এবং right থাকবে। তাহলে আমরা যখন বুঝে যাবো যে আমাদের নতুন node আমাদের root এর চেয়ে বড় নাকি ছোট তখন তো left অথবা right এ পাঠাবো এবং যেদিকেই পাঠাই না কেনো ওইদিকে যাওয়ার আগে আবার চেক করবো যে অইখানে কোনো node আছে নাকি যদি না থাকে তাহলে সরাসরি ওইখানে আমাদের নতুন node বসিয়ে দিবো আর যদি থেকে থাকে তাহলে আমরা আমাদের আগের যে root ছিলো সেটাকে করে দিবো এখন এইখানে থাকা node কে এবং আবার চেক করবো যে এই root এর চেয়ে বড় নাকি ছোট আমাদের নতুন node টি এবং এভাবেই আমাদের node যুক্ত করার প্রসেস চলতে থাকবে এবং ঠিক সেইম ভাবেই right এর দিকে ও।

নিচে কোড দেওয়া হলো এবং সাথে কমেন্ট করে বুঝানো হলো কোন লাইন কি কাজ করছে।

// add node in binary tree

// এখানে একটি টেম্পলেট তৈরি করা হলো নতুন node এর জন্য যাতে পরবর্তীতে যেকোনো জায়গায় ব্যবহার করা যায়।
class Node {
  constructor(value) {
    this.leftChid = null;
    this.rightChild = null;
    this.value = value;
  }
}

class BinaryTree {
  constructor() {
    this.root = null;
  }

  // add method
  addNode(value) {
    // নতুন node একটি variable এ রাখা হলো।
    let newNode = new Node(value);

    // চেক করা হলো যদি root null হয়ে থাকে তাহলে আমাদের root হয়ে যাবে নতুন যে node যুক্ত করতে চাচ্ছি সেটি। আর null না হলে else চলবে।
    if (this.root === null) {
      this.root = newNode;
    } else {
      // currentRoot variable এর মধ্যে আমাদের tree এর যে root রয়েছে তাকে রাখলাম।
      let currentRoot = this.root;

      // এখানে একটি বুলিয়ান value রাখলাম যাতে পরবর্তীতে প্রোগ্রাম রান ব্রেক করতে পারি।
      let added = false;

      // while loop চলবে যদি আমাদের added true না হয় এবং যদি currentRoot null না হয় তাহলে।
      while (!added && currentRoot) {
        // যদি আমাদের নতুন node আমাদের tree এর currentRoot এর value এর চেয়ে ছোট হয় তাহলে
        if (value < currentRoot.value) {
          // যদি আমাদের currentRoot এর left এ কোনো node না থাকে তাহলে
          if (currentRoot.leftChid === null) {
            // currentRoot এর left সমান হয়ে যাবে আমাদের নতুন node
            currentRoot.leftChid = newNode;

            // added কে true করে দিলাম কারণ আমরা নতুন node যুক্ত করে নিলে তো আমাদের আর এই প্রোগ্রাম চালানোর প্রয়োজন নাই তাই।
            added = true;
          }
          // যদি আমাদের currentRoot এর left এ কোনো node থাকে তাহলে
          else {
            // এখন আমাদের currentRoot হয়ে যাবে currenRoot এ থাকা left
            currentRoot = currentRoot.leftChid;
          }
        }
        // যদি আমাদের নতুন node আমাদের tree এর currentRoot এর value থেকে বড় হয় তাহলে
        else if (value > currentRoot.value) {
          // যদি আমাদের currentRoot এর right এ কোনো node না থাকে তাহলে
          if (currentRoot.rightChild === null) {
            // currentRoot এর right সমান হয়ে যাবে আমাদের নতুন node
            currentRoot.rightChild = newNode;

            // added কে true করে দিলাম কারণ আমরা নতুন node যুক্ত করে নিলে তো আমাদের আর এই প্রোগ্রাম চালানোর প্রয়োজন নাই তাই।
            added = true;
          }
          // যদি আমাদের currentRoot এর right এ কোনো node থাকে তাহলে
          else {
            // এখন আমাদের currentRoot হয়ে যাবে currenRoot এ থাকা right
            currentRoot = currentRoot.rightChild;
          }
        }
      }
    }
  }
}

Binary Search Tree - Search Node

> binary tree তে আমরা যেহেতু জানি যে root থেকে left এর দিকে যেসব সংখ্যা থাকবে সেগুলো সব ছোট হবে root এর চেয়ে এবং right এর দিকে যেসব সংখ্যা থাকবে সেগুলো সব বড় হবে root এর চেয়ে তাহলে আমাদের এখানে search করা খুবই সহজ হয়ে গেছে। আমরা প্রথমে চেক করে নিবো আমাদের root আছে কি না যদি থাকে তাহলে বাকি কাজ করবো না হলে সেখানেই রিটার্ন করে দিবো null। আর যদি থাকে তাহলে আমরা যে node টি খুজতে চাচ্ছি সেটা দিয়ে চেক করবো যে আমাদের root এর চেয়ে বড় নাকি ছোট ওই নতুন value টি যদি বড় হয় তাহলে তো আমরা left এর দিকে যাবো না কারণ আমরা জানি ওইদিকে শুধু ছোট সংখ্যাই আছে আমরা যাবো right এর দিকে এবং সেদিকেই আমাদের search node পেয়ে যাবো আর যদি ছোট হয় তাহলে তো left এর দিকে যাবো। ব্যাস এই সিম্পল কাজ আর কিছু না এবং যখন আমাদের search node পেয়ে যাবো তখন সেটা রিটার্ন করে দিবো।

ওকে নিচে কোড দেওয়া হলো এবং সাথে কমেন্ট করে দেওয়া হলো কোন লাইন কি করছে।

// searching node in binary tree
findNode(value) {
    // চেক করা হচ্ছে যদি আমাদের tree তে কোনো node ই না থাকে তাহলে null রিটার্ন করবে।
    if (!this.root) {
      return null;
    }

    // আমাদের বর্তমান root কে একটি variable এর মধ্যে রাখলাম।
    let currentRoot = this.root;

    // আমাদের root যদি থাকে তাহলে এই while loop চলবে।
    while (currentRoot) {

      // চেক করা হচ্ছে যে আমাদের currentRoot এর যে value আছে যেটা কি আমরা যে node খুজছি সেটার সাথে মিলে?
      if (currentRoot.value === value) {
        // মিলে গেলে আমাদের search node এই currentRoot তাই সেটা রিটার্ন করে দিচ্ছি।
        return currentRoot;
      }
      // চেক করা হচ্ছে আমরা যে node খুজছি সেটা কি আমাদের currentRoot এর value এর থেকে ছোট।
      else if (value < currentRoot.value) {
        // ছোট হলে আমাদের currentRoot করে দিবো currentRoot এ থাকা left কে কারণ আমরা জানি যে আমাদের সব ছোট সংখ্যা রয়েছে left এর দিকে।
        currentRoot = currentRoot.leftChid;
      } else {
        // আর বড় হলে আমাদের currentRoot করে দিবো currentRoot এর right কে কারণ ওইদিকে সব বড় সংখ্যা রয়েছে।
        currentRoot = currentRoot.rightChild;
      }
    }
  }