fastDiff

fast (DCT-based) differential

Examples: case 5: use the class in an optimisation. In this example, we have an identity operator, plus gamma times a differential operator. We use a fastDiff method for J and J'.

This involves:

Define some utilities:

 def cost_identity(x,xobs):
   J_ = x - xobs
   J =  0.5 * np.dot(J_,J_)
   return J,J_
   
 def fun_dfun(x,xobs,diff):
   J,J_ = cost_identity(x,xobs)
   J1,J1_ = diff.cost_der_cost(x)
   return J + J1,J_ + J1_

main code

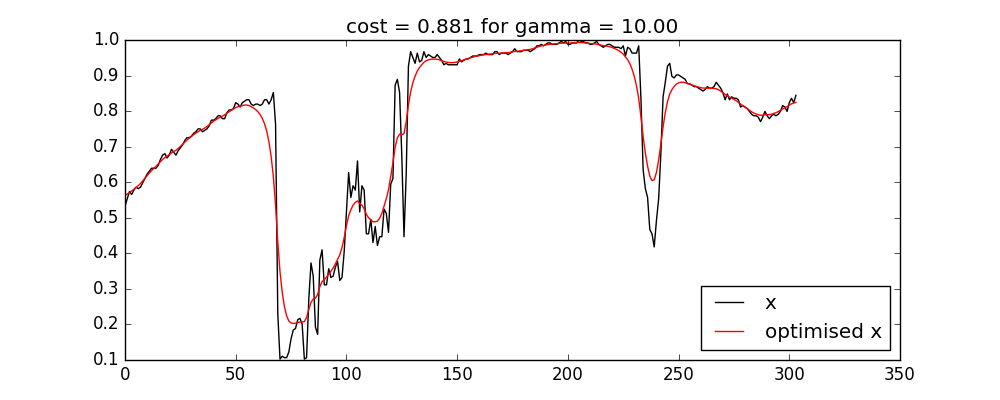
from PIL import Image
import urllib.request
from fastDiff import fastDiff
from scipy.optimize import minimize

# pull a dataset and make it 1D for now
url='https://upload.wikimedia.org/wikipedia/en/0/04/TCF_centre.jpg'
im = np.array(Image.open(urllib.request.urlopen(url)).convert("L")).astype(float)[50]
x = im/im.max()

gamma = 10.
diff = fastDiff(x,axis=(0,),gamma=gamma)
res = minimize(fun_dfun, x, jac=True, method='Newton-CG',\
        options={'disp': True},\
        args=(x,diff))

Result

 Optimization terminated successfully.
   Current function value: 0.881144
   Iterations: 11
   Function evaluations: 12
   Gradient evaluations: 130
   Hessian evaluations: 0

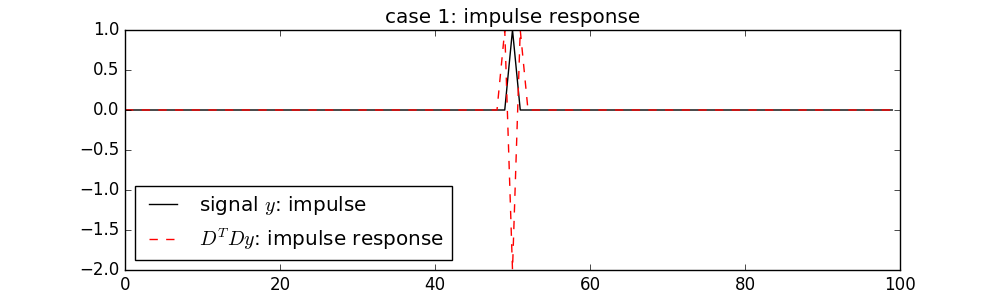
case 1: show impulse response function

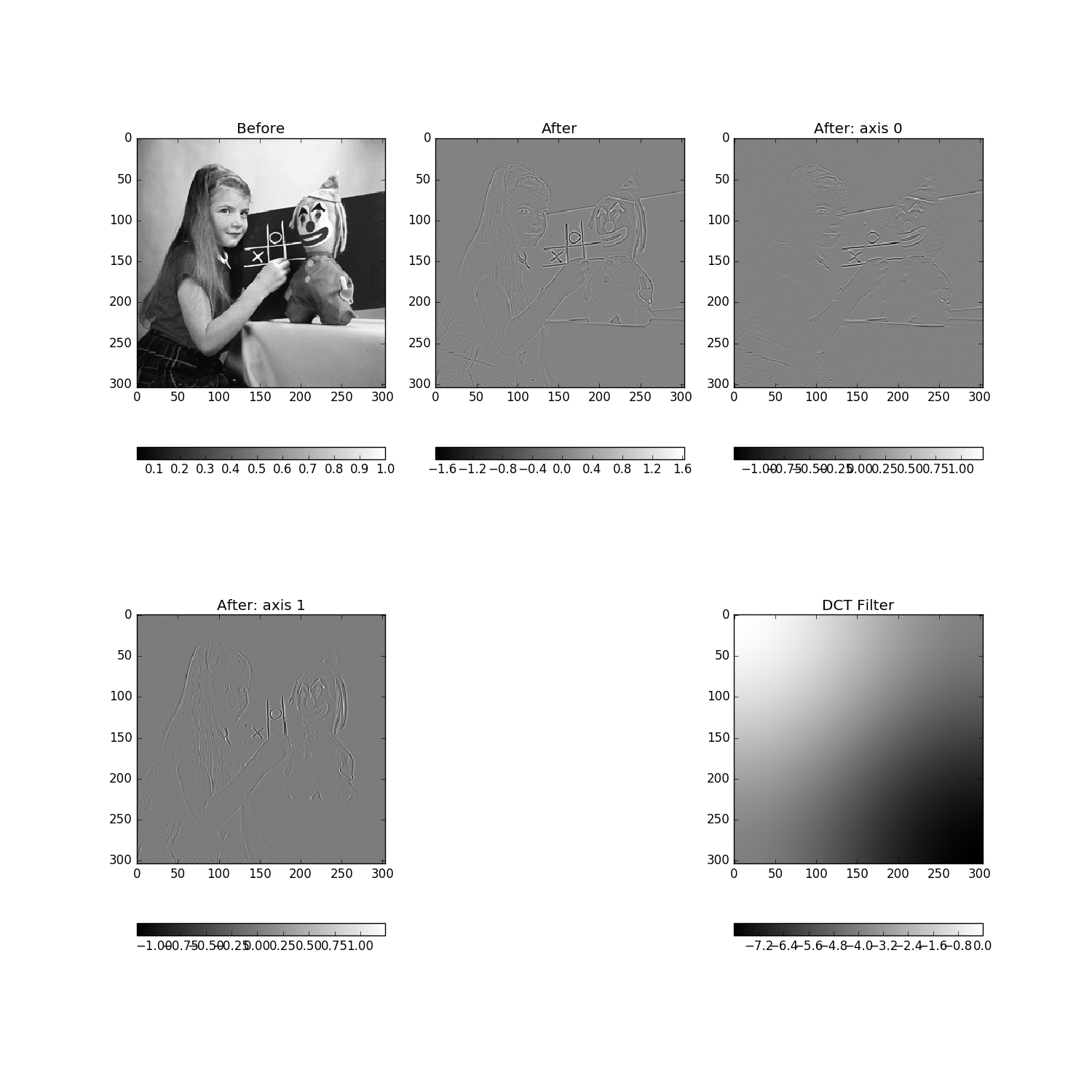
case 2: greyscale image differentiation in one or more dimensions

case 3: colour image differentiation in one or more dimensions

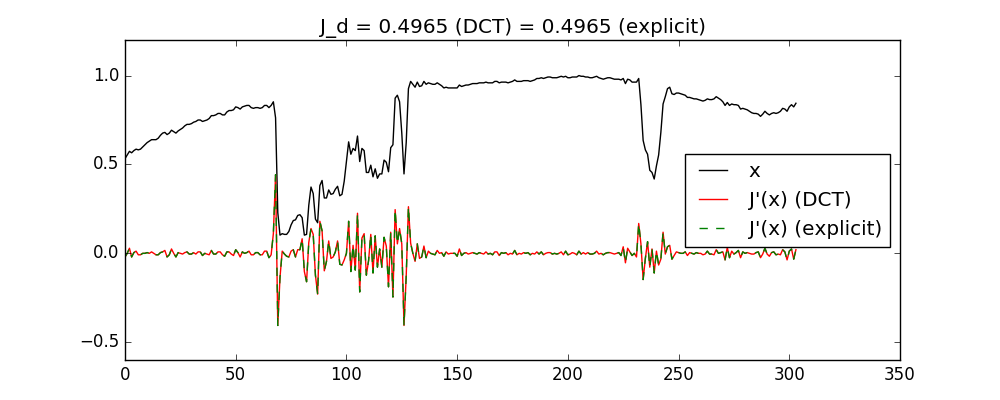
case 4: use to get J and J' for differential operator

profLewis/fastDiff

fastDiff