To get started: Fork this repository then issue
git clone --recursive http://github.com/[username]/geometry-processing-curvature.git
See introduction.
Once built, you can execute the assignment from inside the build/ by running
on a given mesh:
./curvature [path to mesh.obj]
In this assignment we explore discrete curvature quantities computed on a surface. These quantities give us local information about a shape. Beyond inspecting the surface (the extent of this assignment), these quantities become the building blocks to:
- define energies to minimize during smoothing/deformation,
- identify salient points and curves on the shape, and
- provide initial conditions/constraints for remeshing.
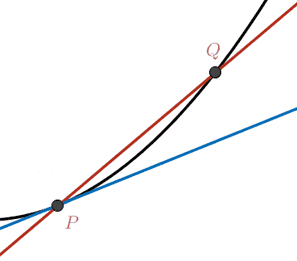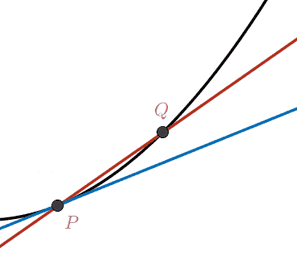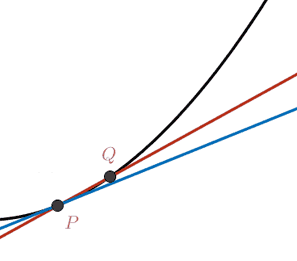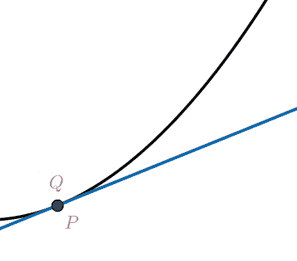
The fundamental difference between a segment on the real line and a curve is the introduction of curvature. This is quite natural and intuitive. When we draw a 1D object in the plane or in space we have the freedom to let that object bend. We quantify this "bending" locally as curvature.
Curvature is also the
fundamental difference between a chunk (i.e., subregion) of the Euclidean
Plane and a
surface that has been
immersed in
We start our discussion assuming a smooth surface
Let us briefly recall how
curvature is
defined for a planar curve
There are multiple equivalent definitions.
We can define the tangent direction at
a point
\[
\t(s) = \lim_{\q→\p} \frac{\q-\p}{|\q-\p|} =
\lim_{t→s} \frac{γ(t)-γ(s)}{|γ(t)-γ(s)|} = \frac{γ'(s)}{|γ'(s)|}.
\]
It always possible, and often convenient, to assume without loss of generality
that
In an analogous fashion, we can consider the limit of the
circumcircle
\[ C(\p) = \lim_{\q₁,\q₂→\p} C(\q₁,\p,\q₂). \]
This limit circle is called the osculating
circle at the point
\[
κ(\p) = \frac{1}{R(\p)}.
\]
The radius is a non-negative measure of length with units meters, so the
curvature
\[ R(\p) = \lim_{\q₁,\q₂→\p} \frac{‖\q₁-\p‖ ‖\p-\q₂‖ ‖\q₂-\q₁‖} {2\left| (\q₁-\p) \quad (\p-\q₂)\right|}. \]
Plugging in our arc-length parameterization this reveals that the curvature (inverse of radius) is equal to the magnitude of change in the tangent or equivalently the magnitude of second derivative of the curve:
\[ κ(s) = \lim_{t→s} \left| \frac{γ'(t)-γ'(s)}{t-s} \right| = ‖γ''(s)‖. \]
Because we chose the arc-length parameterization, the only change to the
tangent vector
\[ γ'' ⋅ γ' = 0 \quad → \quad γ'' ⋅ \hat{\n} = ± κ \hat{\n}. \label{equ:curvature-normal} \]
If we define an orientation to our curve then we can endow the curvature with a sign based on whether the center of the osculating circle lies on the left or right side of the curve. As already established, the tangent of the osculating circle and the curve agree, so the vector pointing toward the circle's center must be perpendicular to the tangent: i.e., in either the positive or negative normal directions.
If the orientation agrees with increasing the arc-length parameter
\[ \begin{align} k(\p) &= \text{sign}(γ''(\p)⋅\hat{\n}))\ κ(\p) \ &= γ''(\p) ⋅ \hat{\n}. \end{align} \]
This definition neatly conforms to our intuition of a curve as the trajectory
of a moving point. Imagine the curved formed by driving along a particular
trajectory
While
Curvature in the path corresponds to turning and quite literally the amount by which your friend needs to turn the steering wheel away from the "straight" position: on a straight course, the steering wheel remains at zero-angle position and the curvature is zero, on a circular course the steering wheel is fixed at a constant angle in the left or right direction corresponding to constant positive or negative curvature respectively.
Changing the steering wheel changes the direction of the vehicle's velocity.
For your friend driving at constant speed, this is the only change admissible
to the velocity, hence the curvature exactly corresponds to
If somebody wants to make a Sega Out Run inspired gif showing a steering wheel turning next to a little car tracing a curve, I'll be very impressed.
The integrated signed curvature around a closed
curve must be an integer multiple of
\[ ∮ k(s) \ ds = 2π τ, \] where τ is an integer called the "turning number" of the curve.
This is a bit surprising at first glance. However, in the moving point
analogy a closed curve corresponds to a period trajectory (e.g., driving
around a race-track). When we've made it once around the track, our velocity
direction (e.g., the direction the vehicle is facing) must be pointing in the
original direction. That is, during the course, the car either have turned all the
way around once (
In the discrete world, if a curve is represented as a piecewise-linear chain of segments, then it's natural to associate curvature with vertices: the segments are flat and therefor contain no curvature.
A natural analog to the definition of curvature as
the derivative of the tangent vector
(i.e.,
\[
k_i = ∠ (\v_i - (\v_{i-1}-\v_i)) \v_i\v_{i+1} = θ_i,
\]
that is, the signed exterior
angle
The turning number theorem for continuous curves finds an immediate analog in
the discrete case. For a closed polygon the discrete signed angles must sum up
to a multiple of
\[ ∑_{i=1}^n k_i = 2π τ. \]
In this way, we preserve the structure found in the continuous case in our discrete analog. This structure preservation leads to an understanding of the exterior angle as an approximation or discrete analog of the locally integrated curvature.
Alternatively, we could literally fit an circle to the discrete curve based on local samples and approximate curvature as the inverse radius of the osculating circle. This curvature measure (in general) will not obey the turning number theorem, but (conducted properly) it will converge to the pointwise continuous values under refinement (e.g., as segment length shrinks).
We will explore these two concepts for surfaces, too: discrete analogs that preserve continuous structures and discretizations that approximate continuous quantities in the limit.
A surface can be curved locally in multiple ways. Consider the difference between a flat piece of paper, a spherical ping-pong ball and a saddle-shaped Pringles chip. The Pringles chip is the most interesting because it curves "outward" in one direction and "inward" in another direction. In this section, we will learn to distinguish and classify points on a surface based on how it curves in each direction.
The simplest way to extend the curvature that we defined for planar curves to a
surface
The (local) intersection of the surface
There are infinitely many planes that pass through a given point
\[ k_\n(φ,\p) = γ''_\n(\p). \]
Normal curvature requires choosing an angle, so it doesn't satiate our desire to reduce the "curvy-ness" to a single number for any point on the surface. A simple way to reduce this space of normal curvatures is to, well, average all possible normal curvatures. This defines the mean curvature:
\[ H(\p) = \frac{1}{2π}∫_0^{2π} k_\n(φ,\p) \ dφ. \]
Another obvious way to reduce the space of normal curvatures to a single number
is to consider the maximum or minimum normal curvature over all choices of
\[ \begin{align} k₁(\p) &= \max_φ \ k_\n(φ,\p) \ k₂(\p) &= \min_φ \ k_\n(φ,\p). \end{align} \]
Collectively, these are referred to as the principal curvatures and correspondingly the angles that maximize and minimize curvature are referred to as the principle curvature directions:
\[ \begin{align} φ₁(\p) &= \argmax_φ \ k_\n(φ,\p) \ φ₂(\p) &= \argmin_φ \ k_\n(φ,\p). \end{align} \]
Euler's
theorem
states that the normal curvature is a quite simple function of
\[ k_\n(φ,\p) = k₁ \cos^2 φ + k₂ \sin^2 φ. \]
There are two immediate and important consequences:
- the principal curvature directions (
$φ₁$ and$φ₂$ ) are orthogonal, and - the mean curvature reduces to the average of principal curvatures:
\[ H = ½(k₁ + k₂). \]
For more theory and a proof of Euler's theorem, I recommend "Elementary Differential Geometry" by Barret O'Neill, Chapter 5.2.
Maximum, minimum and mean curvature reduce curvature to a single number, but still cannot (alone) distinguish between points lying on a round ping-pong ball, a flat sheet of paper, the cylindrical Pringles can and a saddle-shaped Pringles chip.
The neck of this cartoon elephant--like a Pringles chip--bends inward in one
direction (positive
The product of the principal curvatures maintains the disagreement in sign that categories this saddle-like behavior. This product is called Gaussian curvature:
\[ K = k_1 k_2. \]
Both mean and Gaussian curvature have meaningful relationships to surface area.
Let us consider a seemingly unrelated yet familiar problem. Suppose we would
like to minimize the surface area of a given shape
If we consider a small patch
\[
∮_{∂A} -η ;ds = ∮_{∂A} \n × d\x = ∫_A ∆\x ;dA,
\]
where
In the limit as
The Laplacian
\[ ∆f = ∇⋅ ∇f = \tr{ \left[ \begin{array}{cc} \frac{∂²f}{∂u²} & \frac{∂²f}{∂u∂v} \ \frac{∂²f}{∂v∂u} & \frac{∂²f}{∂v²} \end{array} \right] }
\frac{∂²f}{∂u²} + \frac{∂²f}{∂v²}. \]
If we generously choose
\[
\begin{align}
∆\x &= \frac{∂²\x}{∂u²} + \frac{∂²\x}{∂v²} \
&= k₁ \n + k₂ \n \
&= 2H\n,
\end{align}
\]
where
As the product of principal curvatures, Gaussian curvature
Locally, Gaussian curvature measures how far from developable the surface is: how much would the local area need to stretch to become flat.
First, we introduce the Gauss map, a
continuous map
Consider a small patch on a curved surface. Gaussian curvature
\[ K = \lim_{A→0} \frac{A_G}{A}. \label{equ:gaussian-curvature-area} \]
Let's consider different types of regions:
- flat:
$A_G=0$ because the Gauss map is a point, - cylindrical:
$A_G=0$ because the Gauss map is a curve, - spherical:
$A_G>0$ because the Gauss map will maintain positive swept-area, and - saddle-shaped:
$A_G<0$ because the area on the Gauss map will maintain oppositely oriented area (i.e., from the spherical case).
Similar to the turning number theorem for curves, there exists an analogous
theorem for surfaces
stating that the total Gaussian curvature must be an integer multiple of
\[
∫_S K dA = 2π χ(\S),
\label{equ:gauss-bonnet}
\]
where
In stark contrast to mean curvature, this theorem tells us that we cannot add Gaussian curvature to a surface without:
- removing an equal amount some place else, or
- changing the topology of the surface.
Since changing the topology of the surface would require a discontinuous deformation, adding and removing Gaussian curvature must also balance out for smooth deformations. This simultaneously explains why a cloth must have wrinkles when draping over a table, and why a deflated basketball will not lie flat on the ground.
There is yet another way to arrive at principal, mean and Gaussian curvatures.
Consider a point
\[
S_\p(\v) := ∇ \n ⋅ \v
\]
we call
Locally, the tangent vector space is two-dimensional spanned by basis vectors
\[ S_\p(\v) = \left[ \begin{array}{cc} S_\p(\e₁)⋅\e₁ & S_\p(\e₁)⋅\e₂ \ S_\p(\e₂)⋅\e₁ & S_\p(\e₂)⋅\e₂ \end{array} \right] \v \]
Given
\[ S_\p = \left[\r₁ \quad \r₂\right] \left[ \begin{array}{cc} k₁ & 0 \ 0 & k² \end{array} \right] \left[\r₁ \quad \r₂\right]^\transpose \]
Consider why the off-diagonal terms are zero. Think about the extremality of the principal curvatures.
We have actually conducted an eigen decomposition on the shape operator. Reading this progression backwards, the eigen decomposition of the shape operator expressed in any basis will reveal:
- the principal curvatures as the eigen values, and
- the principal curvature directions as the eigen vectors.
By now we are very familiar with the discrete Laplacian for triangle meshes:
\[
∆f ≈ \M^{-1} \L \f,
\]
where
When applied to the vertex positions, this operator gives a point-wise (or rather integral average) approximation of the mean curvature normal:
\[ H\n ≈ \H = \M^{-1} \L \V ∈ \R^{n×3}. \]
Stripping the magnitude off the rows of the resulting matrix would give the
unsigned mean curvature. To make sure that the sign is preserved we can check
whether each row in
This connection between the Laplace operator and the mean curvature normal provides additional understanding for its use as a geometric smoothing operator (see "Computing Discrete Minimal Surfaces and Their Conjugates" [Pinkall and Polthier 1993]).
On a discrete surface represented as a triangle mesh, curvature certainly can't live on the flat faces. Moreover, Gaussian curvature can't live along edges because we can always develop the triangles on either side of an edge to the plane without stretching them. In fact we can develop any arbitrarily long chain of faces connected by edges so long as it doesn't form a loop or contain all faces incident on a vertex. This hints that discrete Gaussian curvature (like curvature for curves) must live at vertices.
Using the definition of Gaussian curvature in terms of the area on the Gauss
map in Equation
\[ Ω_i = 2π - ∑\limits_{f ∈ \text{faces(i)}} θ_{if}. \]
Thus, our discrete analog of locally integrated Gaussian curvature is given
as the angle defect at the
\[ K_i = \frac{2π - ∑\limits_{f ∈ \text{faces(i)}} θ_{if}}{A_i}. \]
By way of closing up the Gauss map, closed polyhedral surfaces (i.e., meshes)
will obey the
Gauss-Bonnet in Equation
\[ ∑\limits_{i=1}^n K_i = 2π χ(\S). \]
We can connect this to Euler's formula for polyhedra in our very first assignment:
\[
\frac{1}{2π} ∑\limits_{i=1}^n K_i = |V| - |E| + |F|,
\]
where
Alternatively, we can approximate all curvatures of a surface by locally fitting an analytic surface and reading off its curvature values. Since planes have no curvature, the simplest type of analytic surface that will give a non-trivial curvature value is a quadratic surface.
Thus, the algorithm proceeds as follows. For each vertex
- gather a sampling of points in the vicinity. For simplicity, let's just
grab all other vertices that share an edge with
$\v$ or share an edge with a vertex that shares an edge with$\v$ (i.e., the "two-ring" of$\v$ ). For most sane meshes, this will provide enough points. Gather the positions of these$k$ points relative to$\v$ (i.e.,$\v_i - \v$ ) into a matrix$\P ∈ \R^{k×3}$ . - Next, we are going to define a quadratic surface as a height field above
some two-dimensional plane passing through
$\v$ . Ideally, the plane is orthogonal to the normal at$\v$ . To find such a plane, compute the principal-component analysis of$\P$ (i.e., conduct eigen decomposition on$\P^\transpose \P$ ). Let$\S ∈ \R^{k × 2}$ be the coefficients for two most principal directions (call them the$u$ - and$v$ - directions) corresponding to each point in$\P$ , and let$\B ∈ \R^{k}$ be the "height" of each point in the least principal direction (call it the$w$ -direction). - An quadratic function as a height-field surface passing through the origin
is given by:
\[
w = a₁ u + a₂ v + a₃ u² + a₄uv + a₅v².
\]
We have
$k$ sets of$u,v$ values and$w$ values. Treat this as a least-squares fitting problem and solve for the 5 unknown coefficients. (igl::pinvis good for solving this robustly). - Each element of the shape operator for the graph of a quadratic function over the plane has a closed form expression. You need to derive these by hand. Just kidding. The shape operator can be constructed as the product of two matrices: \[ S = - \left[ \begin{array}{cc} e & f \ f & g \end{array} \right] \left[ \begin{array}{cc} E & F \ F & G \end{array} \right]^{-1} \] known as the second and first fundamental forms respectively. The entries of these matrices categorize the stretch and bending in each direction: \[ E = 1+a₁² \ F = a₁a₂ \ G = 1+a₂² \ e = \frac{2a₃}{\sqrt{a₁² + 1 + a₂²}} \ f = \frac{a₄}{\sqrt{a₁² + 1 + a₂²}} \ g = \frac{2a₅}{\sqrt{a₁² + 1 + a₂²}} \] See Table 1 of "Estimating Differential Quantities Using Polynomial Fitting of Osculating Jets" [Cazals & Pouget 2003] to double check for typos :-).
- Eigen decomposition of
$S$ reveals the principal curvatures$k₁$ and$k₂$ and the principal tangent directions (in the$uv$ PCA basis). - Lift the principal tangent directions back to world
$\R³$ coordinates.
Download Barret O'Neill's book. This is my go-to differential geometry book. The section on curvature and the shape operator should help resolve questions and fill in missing proofs above.
igl::gaussian_curvatureigl::internal_angles(or any of the other overloads)igl::principal_curvatures
igl::adjacency_matrix.higl::cotmatrixigl::invert_diagigl::massmatrixigl::per_vertex_normalsigl::pinvigl::sliceigl::sortigl::squared_edge_lengths
Compute the discrete mean curvature at each vertex of a mesh (V,F) by
taking the signed magnitude of the mean curvature normal as a pointwise (or
integral average) quantity.
Given (squared) edge-lengths of a triangle mesh l_sqr compute the internal
angles at each corner (a.k.a. wedge) of the mesh.
Compute the discrete angle defect at each vertex of a triangle mesh
(V,F), that is, the locally integrated discrete Gaussian
curvature.
Approximate principal curvature values and directions locally by considering
the two-ring neighborhood of each vertex in the mesh (V,F).




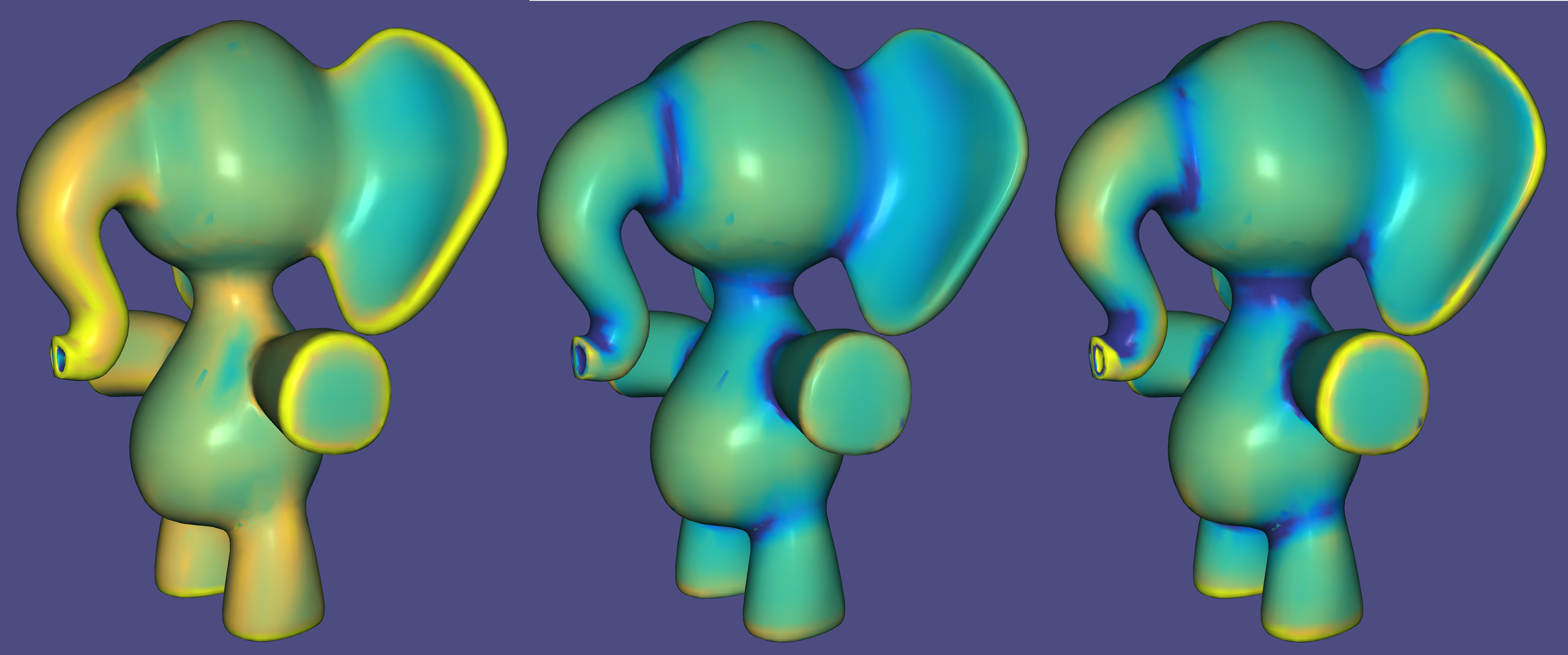




!["Gaussian Curvature and Shell Structures" [Calladine 1986]](https://raw.githubusercontent.com/psarahdactyl/geometry-processing-curvature/master/images/angle-defect.png)