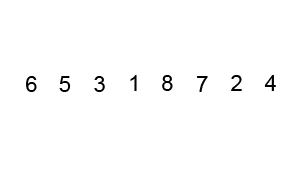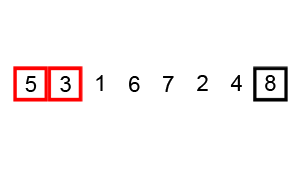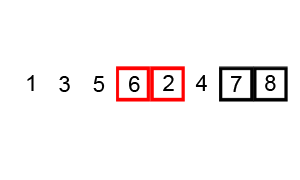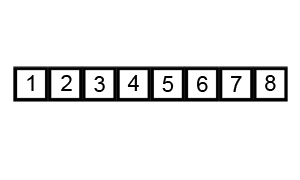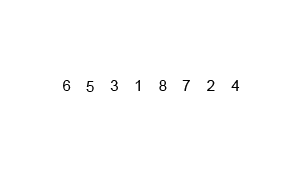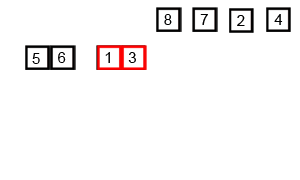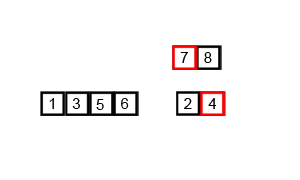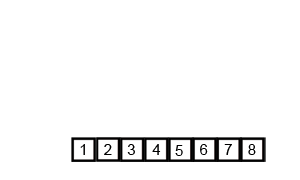Week 5 workshop - Sorting and efficiency

In Python, sorting a list is as easy as running sorted(). But what is behind that command? How does it work?

There are many different algorithms available to sort elements by increasing (or decreasing) value, some more efficient than others. Today, we'll implement a few of them, and through them, introduce the concept of computational efficiency, and how to evaluate it in Python. This should also be a good exercise for you to practice your algorithmic skills.

This is a pair programming workshop, so pick someone to be the driver first, and swap roles every 15 minutes or so.

Task 1: Bubble sort

Bubble sort has a fairly simple implementation: each pair of consecutive elements is put in order one by one, until the whole list is sorted. This usually requires multiple passes over a list until it's fully sorted. The larger elements will "bubble up" to the end of the list as you go along.

Start at the first element in the list.
- Compare it to the next element.
- If these 2 elements are in the wrong order, swap them.
- Move to the next element of the list.
Repeat the steps in 1. until reaching the end of the list.
Repeat steps 1 and 2 until you can go through the list without having swapped any elements -- this means that the list is now sorted.

Write a function bubble_sort() which takes such a list as an input, and returns another list where the elements have been sorted using bubble sort.

You can test your function using Numpy's np.random module to create an array random_array of random integers of some length n, ranging from 1 to n. Compare the output of your bubble_sort() function with the output of Python's sorted() function on the same array. The Numpy documentation, as always, will be useful.

A quick note on mutable types and operating in-place

Mutable objects are objects that you can modify in-place in Python. There is a fairly detailed explanation of this in the Week 3 code-along video (the bin-packing problem). Lists and Numpy arrays, for example, are mutable; strings are not. (Try it -- create a string s, and try to change the first character afterwards with s[0] = 'x'.)

A function can change mutable objects in-place -- it can actually go look in memory for the box where the data is stored, and change the contents. Here is an example you can run to convince yourself -- note that we are not returning anything, the list my_list is changed in-place.

my_list = [5, 5, 5, 5, 5]

def my_func(some_list):
    some_list[1] = 999

# Note that the function doesn't return anything, and here we don't assign any new variables either
my_func(my_list)
print(my_list)

This can be a good way to implement a function which changes an array or a list, but the issue here is that we lose the original list permanently. Alternatively, if we want to keep both (which could be useful here to compare with sorted()), we can use the .copy() method to create a copy of the array -- and now we need to return it:

my_list = [5, 5, 5, 5, 5]

def my_func(some_list):
    new_list = some_list.copy()
    new_list[1] = 999
    return new_list

my_new_list = my_func(my_list)
print(my_list)  # Now the same as before
print(my_new_list)

Note that .copy() works on both lists and Numpy arrays.

Task 2: Evaluating the performance of bubble sort

Despite being quite simple to implement, bubble sort is not generally used to sort large arrays, because it is not efficient -- it passes over the whole list many times to fully sort it. In fact, as the size of the list grows, not only the time it takes to go through the list increases, but also the number of passes it has to do over the whole list! In fact, it's possible to show that when the size n of a list increases, the time it takes to sort that list with bubble sort increases as fast as n^2. We say that bubble sort has time complexity O(n^2) (this is the "big O" notation).

One of the main aspects of computational efficiency of an algorithm is this time complexity -- in other words, how fast it is, and how the speed changes when dealing with bigger problems (another important aspect is memory efficiency -- we'll talk about this later in the course). In virtually every computational application in scientific computing or data science, you will be dealing with large amounts of data, and implementing efficient algorithms will be imperative.

A quick way to evaluate efficiency in Python is to use the time module -- specifically, its time() and time_ns() functions. For instance, time.time() returns the current time (in seconds, since 1970). While not very useful on its own, you can use two time.time() calls to measure elapsed time. Try this:

import time
t0 = time.time()
time.sleep(3)   # Tell Python to wait 3 seconds
t1 = time.time() - t0
print(f'Time elapsed: {t1} seconds')

Now, let's measure the time it takes for bubble_sort() to sort lists of different sizes. Write a function time_sort() which executes bubble_sort() on random lists of size 500 to 3000, with increments of 500. Your function should time the execution of bubble_sort() every time (note that you don't need to store the result here), and finally plot 6 points on a graph, where the x-axis is the array size and the y-axis is the measured computation time.

You should see that the points form a parabola, indicating O(n^2). If your computer can take it, don't hesitate to try larger values of n (up to, say, 10000). If you plot the results on a log-log scale, you should see a straight line with slope 2, again indicating O(n^2).

Task 3: Merge sort

As opposed to bubble sort, merge sort is one of the most efficient sorting algorithms. It is recursive, and uses a "divide and conquer" method: a list is split into 2 halves, each half is itself divided into 2 halves, etc., until we reach lists of length 1, which is (by default) sorted. Then, we merge these half-lists again all the way back until we have the full list again, now sorted.

Here are the steps:

Split the list in half.
For each half, if it has length 1, then it's sorted; otherwise, merge sort it (recursively; split it in half, etc.).
Merge the two (now sorted) halves, by comparing the first elements in each list pair-wise and adding the smallest to the new list every time.

For example, to merge the lists [3, 7, 8] and [4, 5, 11]:

compare 3 and 4, add 3 to the list.
- new list: [3]
- remaining: [7, 8] and [4, 5, 11]
compare 7 and 4, add 4 to the list.
- new list: [3, 4]
- remaining: [7, 8] and [5, 11]
compare 7 and 5, add 5 to the list.
- new list: [3, 4, 5]
- remaining: [7, 8] and [11]
etc.

Write a function merge() to merge 2 sorted lists as described above and return the sorted list. Then, write a recursive function merge_sort() to implement merge sort, calling your function merge() for the merging step.

Modify your previous function time_sort() to take a function as an input argument, and use it to evaluate the performance of merge_sort() as you did for bubble_sort(). This should be much faster than bubble_sort() for larger arrays, so you could time execution for larger sizes, or call the function multiple times on the same array and compute the average time to get more stable results (make sure you don't change in-place if you do this, otherwise the second time around, the list will already be sorted!).

Extra reading for the curious

Although, for practical applications, we usually want the most efficient algorithm, finding the least efficient ways one could go about sorting a list of numbers is also an interesting exercise, and has led to some very creative answers -- see, for example, this forum thread, or this paper describing Slowsort, which prefers "multiply and surrender" to "divide and conquer".

There are some great visualisations of sorting algorithms here and here (with audio!). (The source code used to generate that video is available on GitHub.)

Attribution

Bubble sort and Merge sort animations: Swfung8, CC BY-SA 3.0, via Wikimedia Commons

pypr-2021/w05-workshop