Fracdiff: Super-fast Fractional Differentiation

Fracdiff performs fractional differentiation of time-series, a la "Advances in Financial Machine Learning" by M. Prado. Fractional differentiation processes time-series to a stationary one while preserving memory in the original time-series. Fracdiff features super-fast computation and scikit-learn compatible API.

What is fractional differentiation?

See M. L. Prado, "Advances in Financial Machine Learning".

Installation

$ pip install fracdiff

Features

Functionalities

fdiff: A function which extends numpy.diff to fractional orders.
Fracdiff: Perform fracdiff of a set of time-series. Compatible with scikit-learn API.
FracdiffStat: Automatically fracdiff which makes a set of time-series stationary while preserving their maximum memory. Compatible with scikit-learn API.

Speed

Fracdiff is blazingly fast.

The following graphs show that Fracdiff computes fractional differentiation much faster than the "official" implementation.

It is especially noteworthy that execution time does not increase significantly as the number of time-steps (n_samples) increases, thanks to NumPy engine.

The following tables of execution times (in unit of ms) show that Fracdiff can be ~10000 times faster than the "official" implementation.

n_samples	fracdiff	official
100	0.164 +- 0.088	20.725 +- 5.323
1000	0.162 +- 0.055	108.049 +- 3.612
10000	0.268 +- 0.085	1074.970 +- 89.375
100000	0.779 +- 0.241	12418.813 +- 453.551

n_features	fracdiff	official
1	0.162 +- 0.055	108.049 +- 3.612
10	0.229 +- 0.036	1395.027 +- 172.948
100	1.745 +- 0.196	13820.834 +- 821.352
1000	19.438 +- 2.093	154178.162 +- 11141.337

(Run on Macbook Air 2018, 1.6 GHz Dual-Core Intel Core i5, 16 GB 2133 MHz LPDDR3)

How to use

Fractional differentiation

A function fdiff calculates fractional differentiation. This is an extension of numpy.diff to a fractional order.

import numpy as np
from fracdiff import fdiff

a = np.array([1, 2, 4, 7, 0])
fdiff(a, n=0.5)
# array([ 1.       ,  1.5      ,  2.875    ,  4.6875   , -4.1640625])
np.array_equal(fdiff(a, n=1), np.diff(a, n=1))
# True

a = np.array([[1, 3, 6, 10], [0, 5, 6, 8]])
fdiff(a, n=0.5, axis=0)
# array([[ 1. ,  3. ,  6. , 10. ],
#        [-0.5,  3.5,  3. ,  3. ]])
fdiff(a, n=0.5, axis=-1)
# array([[1.    , 2.5   , 4.375 , 6.5625],
#        [0.    , 5.    , 3.5   , 4.375 ]])

Preprocessing by fractional differentiation

A transformer class Fracdiff performs fractional differentiation by its method transform.

from fracdiff import Fracdiff

X = ...  # 2d time-series with shape (n_samples, n_features)

f = Fracdiff(0.5)
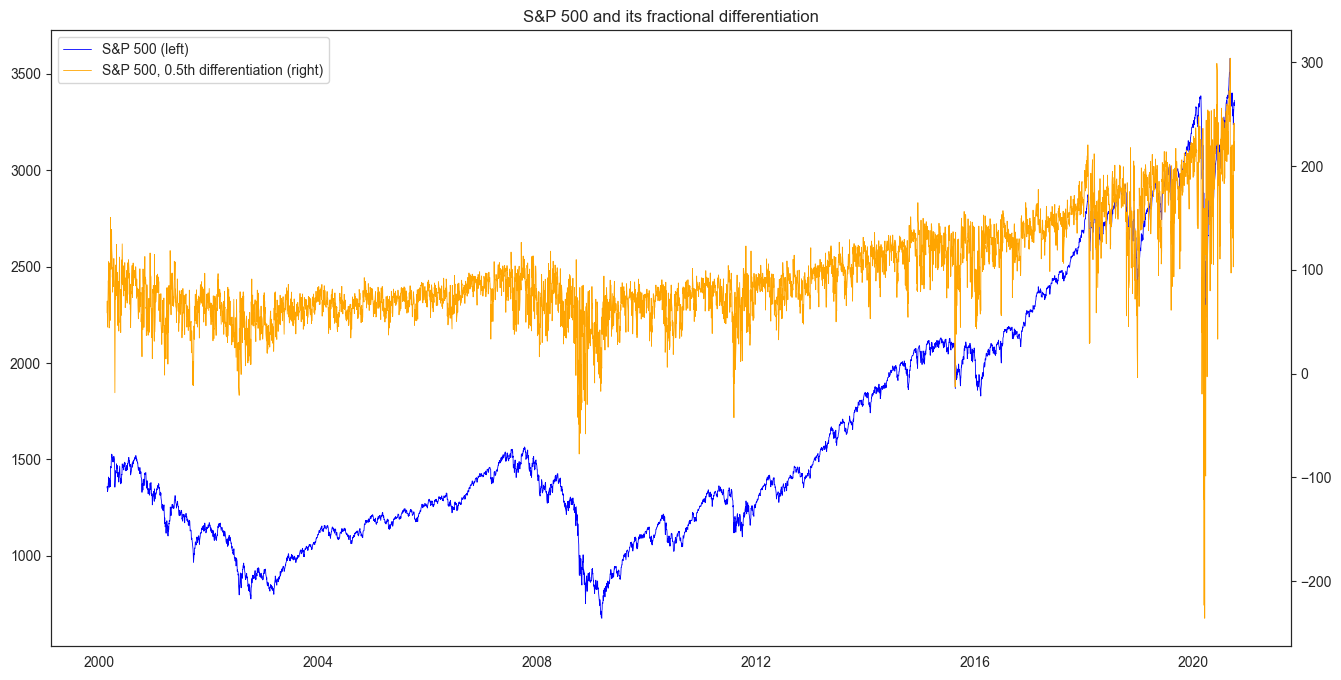
X = f.fit_transform(X)

For example, 0.5th differentiation of S&P 500 historical price looks like this:

Fracdiff is compatible with scikit-learn API. One can imcorporate it into a pipeline.

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

X, y = ...  # Dataset

pipeline = Pipeline([
    ('scaler', StandardScaler()),
    ('fracdiff', Fracdiff(0.5)),
    ('regressor', LinearRegression()),
])
pipeline.fit(X, y)

Fractional differentiation while preserving memory

A transformer class FracdiffStat finds the minumum order of fractional differentiation that makes time-series stationary. Differentiated time-series with this order is obtained by subsequently applying transform method. This series is interpreted as a stationary time-series keeping the maximum memory of the original time-series.

from fracdiff import FracdiffStat

X = ...  # 2d time-series with shape (n_samples, n_features)

f = FracdiffStat()
X = f.fit_transform(X)
f.d_
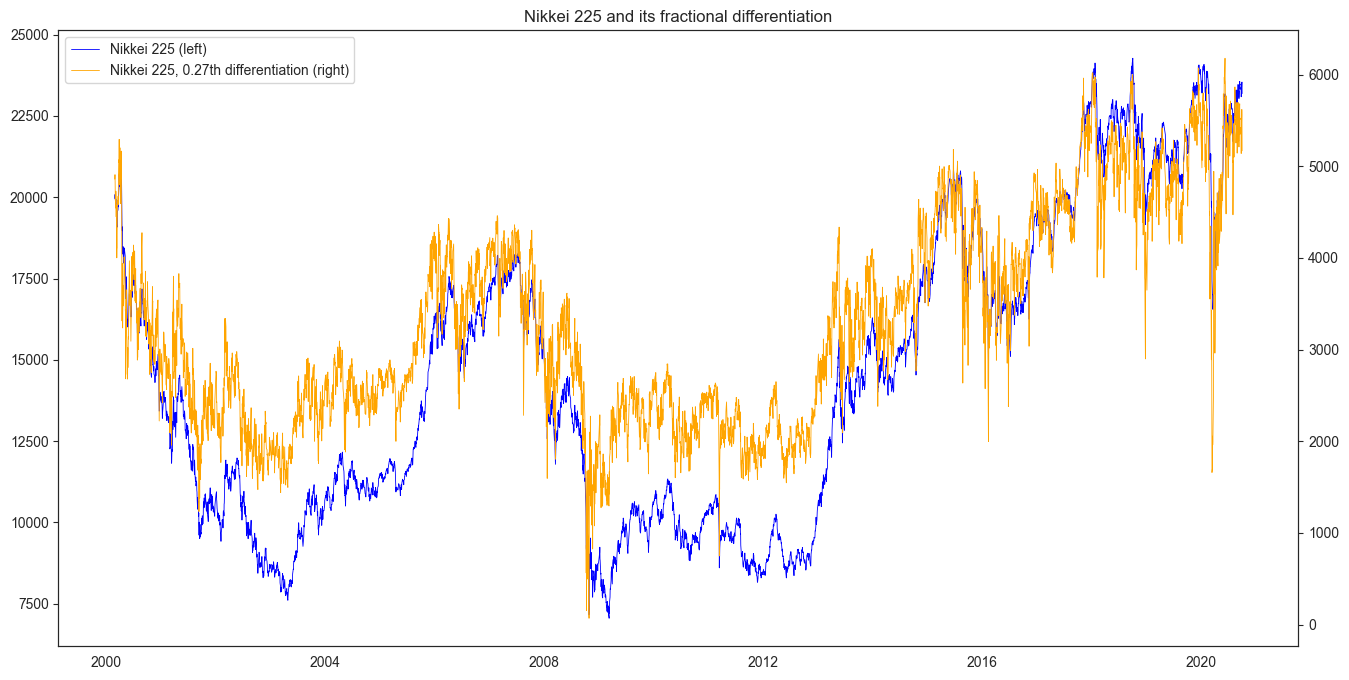
# array([0.71875 , 0.609375, 0.515625])

The result for Nikkei 225 index historical price looks like this:

Other examples are provided here.

Example solutions of exercises in Section 5 of "Advances in Financial Machine Learning" are provided here.

References

Marcos Lopez de Prado, "Advances in Financial Machine Learning", Wiley, (2018).

qcho1010/fracdiff