Qlasskit

Qlasskit is a Python library that allows quantum developers to write classical algorithms in pure Python and translate them into unitary operators (gates) for use in quantum circuits, using boolean expressions as intermediate form.

This tool will be useful for any algorithm that relies on a 'blackbox' function and for describing the classical components of a quantum algorithm.

Qlasskit implements circuit / gate exporters for Qiskit, Cirq, Qasm and Sympy.

pip install qlasskit

For a quickstart, read the quickstart and examples notebooks from the documentation: https://dakk.github.io/qlasskit.

from qlasskit import qlassf, Qint4 

@qlassf
def h(k: Qint4) -> bool:
    h = True
    for i in range(4):
        h = h and k[i]
    return h

Qlasskit will take care of translating the function to boolean expressions, simplify them and translate to a quantum circuit.

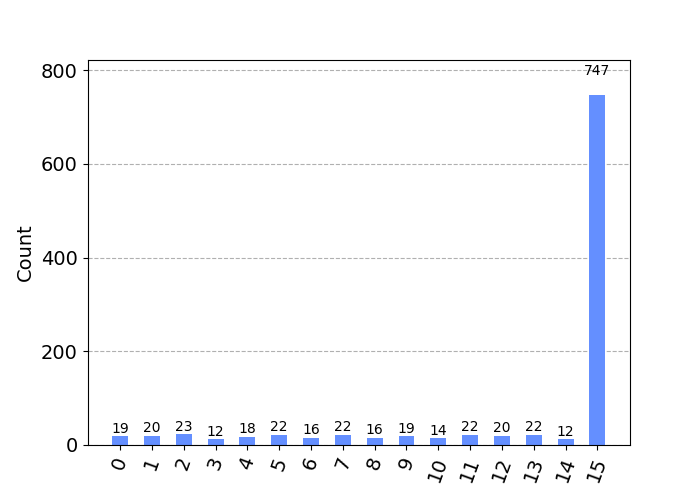
Then, we can use grover to find which h(k) returns True:

from qlasskit.algorithms import Grover

algo = Grover(h, True)
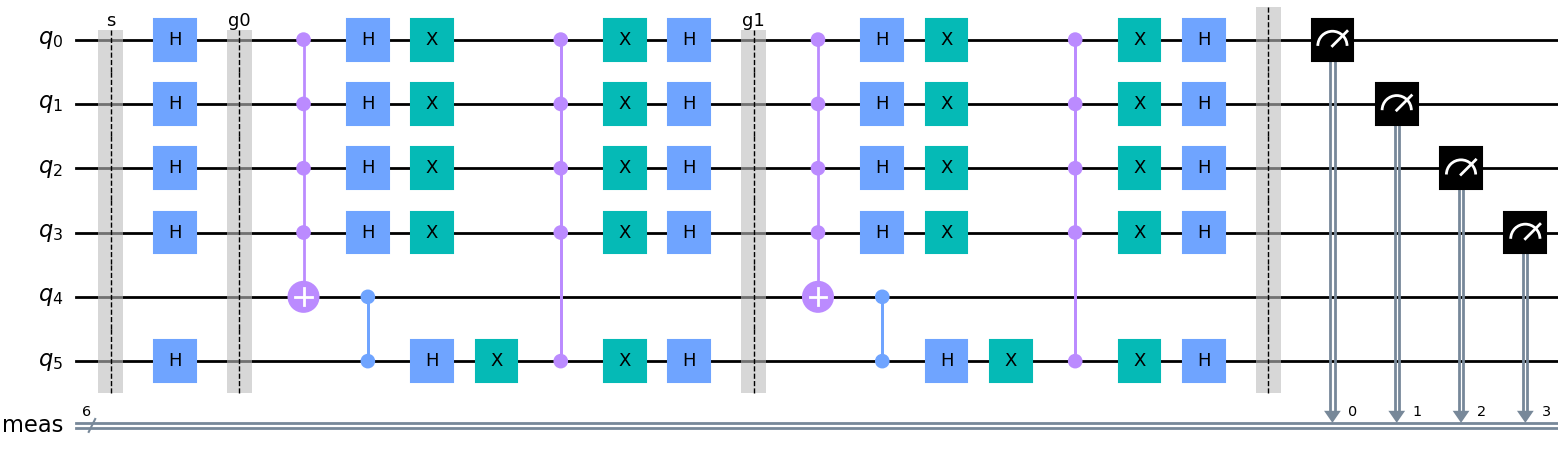
qc = algo.circuit().export("circuit", "qiskit")

And that's the result:

Qlasskit also offers type abstraction for encoding inputs and decoding results:

counts_readable = algo.decode_counts(counts)
plot_histogram(counts_readable)

You can also use other functions inside a qlassf:

@qlassf
def equal_8(n: Qint4) -> bool:
  return equal_8 == 8

@qlassf
def f(n: Qint4) -> bool:
  n = n+1 if equal_8(n) else n
  return n

Qlasskit supports complex data types, like tuples and fixed size lists:

@qlassf
def f(a: Tuple[Qint8, Qint8]) -> Tuple[bool, bool]:
  return a[0] == 42, a[1] == 0

@qlassf
def search(alist: Qlist[Qint2, 4], to_search: Qint2):
  for x in alist:
    if x == to_search:
      return True
  return False

Roadmap

Read TODO for details about the roadmap and TODOs.

Contributing

Read CONTRIBUTING for details.

License

This software is licensed with Apache License 2.0.

Cite

@software{qlasskit2023,
  author = {Davide Gessa},
  title = {qlasskit: a python-to-quantum circuit compiler},
  url = {https://github.com/dakk/qlasskit},
  year = {2023},
}

About the author