The goal of {fluents} is to be an opinionated R package
re-implementation of grind.R by
Rob de Boer, Theoretical Biology and Bioinformatics, University of
Utrecht. grind.R is a port from the same author C-based program GRIND
(GReat INtegrator Differential
equations) to R.
{fluents} aims at packing the same functionality as grind.R,
departing from grind.R in a few ways:
{fluents}is an R package,grind.Ris a script.{fluents}is under public version control at GitHub, facilitating open collaboration and easy distribution.{fluents}’s API has more functions that do less each, whilegrind.R’s has fewer functions that do more each.
You can install the current version of {fluents} with:
# install.packages("remotes")
remotes::install_github("ramiromagno/fluents")library(fluents)
#>
#> Attaching package: 'fluents'
#> The following object is masked from 'package:base':
#>
#> solve
# `m`: Lotka-Volterra model
m <- function(t, state, parms) {
with(as.list(c(state, parms)), {
dR <- r * R * (1 - R / K) - a * R * N
dN <- c * a * R * N - delta * N
return(list(c(dR, dN)))
})
}
# `p`: vector of parameters
p <- c(
r = 1,
K = 1,
a = 1,
c = 1,
delta = 0.5
)
# `s`: vector of initial state
s <- c(R = 1, N = 0.01)
# `t`: time points
t <- seq(0, 100, by= 1)
# Integrate the ODE
sol <- solve(s = s, p = p, m = m, t = t)
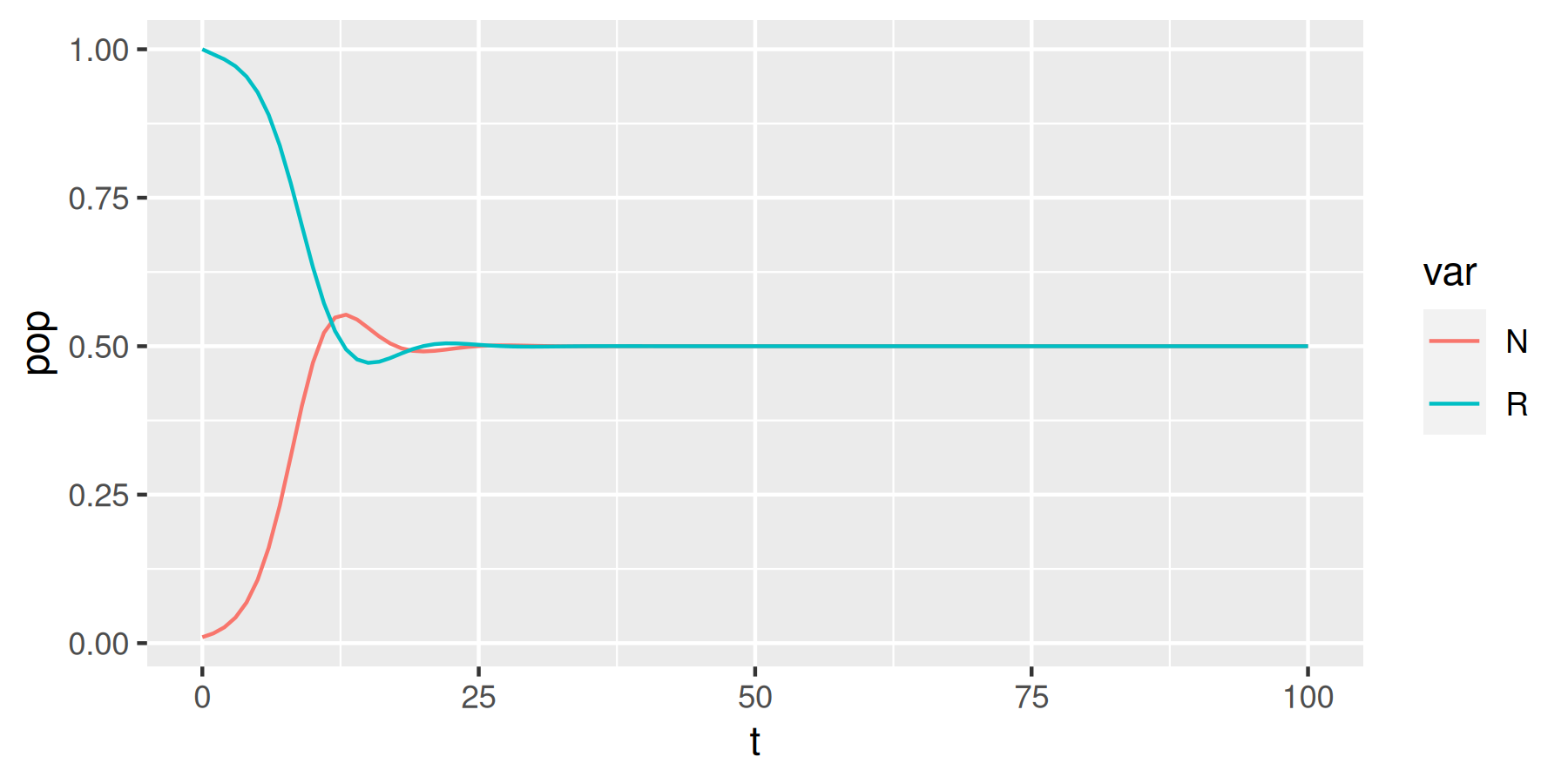
# Make a time plot of the solution `sol`
tidyr::pivot_longer(sol, cols = c("R", "N"), names_to = "var", values_to = "pop") %>%
ggplot(aes(x = t, y = pop, col = var)) +
geom_line()# Find steady states
steady_states(
s0 = tidyr::expand_grid(R = seq(0, 1, 0.1), N = seq(0, 1, 0.1)),
p = p,
m = m
)
#> diagonal element is zero
#> [1] 2
#> diagonal element is zero
#> [1] 2
#> # A tibble: 3 × 8
#> ..R ..N R N stability jacobian eigenvalues eigenvectors
#> <dbl> <dbl> <dbl> <dbl> <chr> <list> <list> <list>
#> 1 0 0 0 0 unstable <dbl [2 × 2]> <dbl [2]> <dbl [2 × 2]>
#> 2 0.1 0.8 0.5 0.5 stable <dbl [2 × 2]> <cpl [2]> <cpl [2 × 2]>
#> 3 0.3 0.2 1 0 unstable <dbl [2 × 2]> <dbl [2]> <dbl [2 × 2]>| grind.R | fluents |
|---|---|
run() |
solve() |
newton() |
steady_states() |