Better to be Lucky than Good? A Wordle Analysis

Introduction

In the rapidly growing landscape of online word games, Wordle has emerged as a popular and engaging daily challenge that tests players’ vocabulary, deduction, and strategy. The objective is simple: guess a hidden five-letter word within six attempts, using color-coded feedback to inform subsequent guesses. While success in Wordle might seem to hinge on a combination of vocabulary breadth and strategic reasoning, this study investigates a less intuitive factor—luck.

This analysis explores the relative contributions of luck and skill to Wordle performance. Using a dataset of Wordle games, we employ an R-based analysis to measure how each player’s skill and luck scores correlate with the number of guesses required to solve the puzzle.

Methods

The data for this study is drawn from a Facebook messenger chat between college friends. This chat contains shared Wordle results dating back to March 2022. A data request was made to Facebook to download the entire chat in HTML so that messages containing Wordle results could be extracted. The consent of all parties who shared the results of scored Wordle games between March 2022 and August 2024 was obtained prior to publication. This study was exempted from IRB review by not being submitted to an IRB.

Analysis was performed in R 4.4.1 using the code below. A total of 2297 observations were extracted using regex from the chat, of which 279 had valid Skill, Luck, and Guess data (12.1%). The remaining observations were shared with out Skill and Luck scores either because they predated the inclusion of those scores or because users shared results from the main Wordle landing page and not from the Wordlebot analyzer.

Analysis

First we load the necessary libraries. We then import the group chat data from a file called message_1.html. This raw source data is not shared on GitHub to maintain privacy of group member communications.

# Load necessary libraries
library(rvest)
library(dplyr)
library(magrittr)
library(stringr)
library(future)
library(furrr)
library(ggplot2)
library(tidyr)
library(lubridate)

# Load the HTML file

on.hpc = FALSE

if(on.hpc){
  file_path = "message_1.html"
} else {
  file_path = "C:\\Users\\saiee\\OneDrive\\Documents\\_Northwestern Residency\\Research\\Miscellaneous Analyses\\message_1.html" #URL on PC
}

page <- read_html(file_path)

# Extract the text content from the HTML
text_content <- page %>% html_text()

# Split the text content into individual lines
lines <- str_split(text_content, "(?=Wordle )") %>% .[[1]]

# Loop through each line to find and extract Wordle data
params <- list('i' = seq(2,length(lines)))

We then create a function calc_row for examining a single line of html from the chat. This function assesses whether the line contains a Wordle post. If it does, then it extracts that Wordle data and create a row of data summarizing the Wordle post. If not, it returns an NA row.

calc_row <- function(i) {
  line <- str_trim(lines[i]) %>% {sub(',','',.)}
  
  # Check if the line contains a Wordle result
  if (str_detect(line, "\\d+ \\d/6")) {
    # Extract the Wordle number, guesses, and user
    wordle_number <- str_extract(line, "Wordle \\d+") %>% str_extract("\\d+") %>% as.numeric()
    guess <- str_extract(line, "\\d/6") %>% str_extract("\\d") %>% as.numeric()
    user <- word(lines[i-1],-1)

    # Find the WordleBot skill and luck scores in the following lines
    skill <- str_extract(line, "Skill \\d+/99") %>% str_extract("\\d+") %>% as.numeric()
    luck <- str_extract(line, "Luck \\d+/99") %>% str_extract("\\d+") %>% as.numeric()
    
    # Extract the date from two lines above the Wordle result
    date <- str_trim(line) %>% str_extract("[A-Za-z]{3} \\d{1,2}, \\d{4}")

    wordle_data <- data.frame(
      'Date' = date,
      'User' = user,
      'Wordle' = wordle_number,
      'Guesses' = guess,
      'Skill' = skill,
      'Luck' = luck,
      stringsAsFactors = FALSE
    )
  } else {
    wordle_data <- data.frame(
      'Date' = NA,
      'User' = NA,
      'Wordle' = NA,
      'Guesses' = NA,
      'Skill' = NA,
      'Luck' = NA,
      stringsAsFactors = FALSE
    )
  }
  
  return(wordle_data)
  
  
}

The next chunk plans and executes the parallel computing process using library functions from the furrr package. The code runs calc_row on each line of text, collects the results as a list of N 1x6 data frames, and combines the rows to make an Nx6 data frame and saves the data to a CSV file.

plan(multicore, workers = 3)
wordle <- future_pmap(params, calc_row, .progress = TRUE) %>%
  bind_rows()

# now save the data to a csv

write.csv(wordle, file = 'wordle_data.csv')

We then clean the data. Data cleaning steps are explained in in-line comments.

# Some 'users' identified in calc_row(...) are actually just random words.
# Here I extract names of real users on the basis that their names are 
# capitalized. I could have hard-coded vector of my friends' names,
# e.g., c('Alex','Hector', etc.), but I am keeping them anonymous in the
# source code shared on GitHub

real_user_names <- wordle %>%
  pull(User) %>%
  unique() %>%
  {.[c(grepl("^[A-Za-z]+$",substr(.,1,1)) &
         substr(.,1,1) == substr(toupper(.),1,1))]}

# my friends names in the graphs and figures will be replaced by those below
# obtained from https://1000randomnames.com/
replacement_names <- c('River Edwards','Adrian Hawkins','Ariel O’Connell',
                       'Jovanni Woodward','Drew Norris','Cairo Adkins',
                       'Emelia McPherson','Foster Reid','Charlee Salas',
                       'Zaiden Gallagher','Elliott Dejesus','Rio Bailey')

# Recode the 'guesses' values as a factor variable,
# filter to include posts only by real_user_names,
# fill in missing dates with the adjacent dates,
# and parse the dates (strings) to lubridate dates

wordle %<>% 
  mutate(Guesses = Guesses %>% as.factor()) %>% 
  filter(User %in% real_user_names) %>% 
  fill(Date) %>% 
  mutate(Date = Date %>% mdy())

# replace my friends' names with the anonymous replacement names
wordle$User = replacement_names[wordle$User %>% as.factor()]

# save the dataset again for sharing on GitHub after names have been anonymized
write.csv(wordle, 'wordle_data_anonymized.csv')

# keep only posts with valid guess data
wordle %<>% filter(!is.na(Guesses))

Results

Now for fun time. Let’s make some plots. Each graph will show N = 279 points.

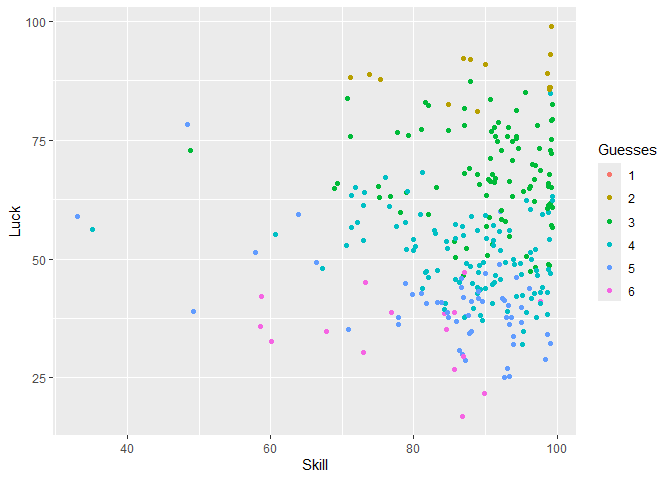
First, here is a scatter plot of skill vs. luck scores, color coded by the number of guesses required to solve the puzzle:

wordle %>% ggplot(aes(color = Guesses, x = Skill, y = Luck)) +
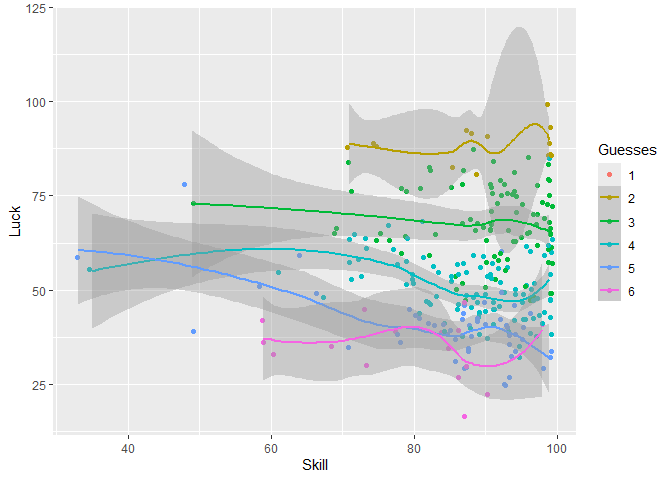
  geom_jitter()

Here is the same graph but overlaid with LOESS curves to show the estimated averages and confidence intervals:

wordle %>% ggplot(aes(color = Guesses, x = Skill, y = Luck)) +
  geom_jitter() + 
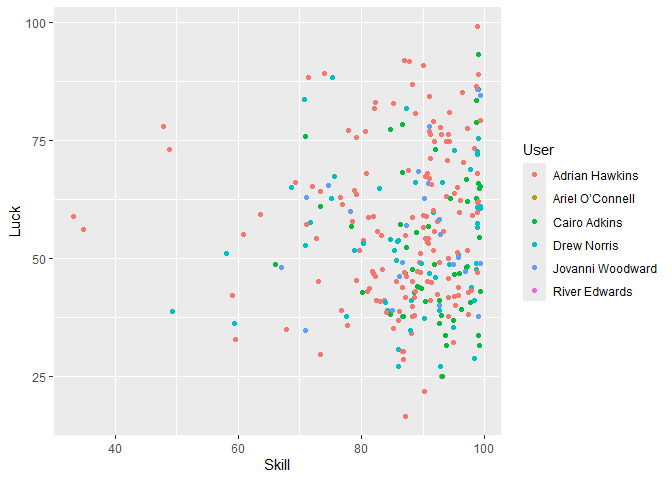
  geom_smooth(method = 'loess')

Next for fun, here is the scatter plot color coded by user:

wordle %>% ggplot(aes(color = User, x = Skill, y = Luck)) +
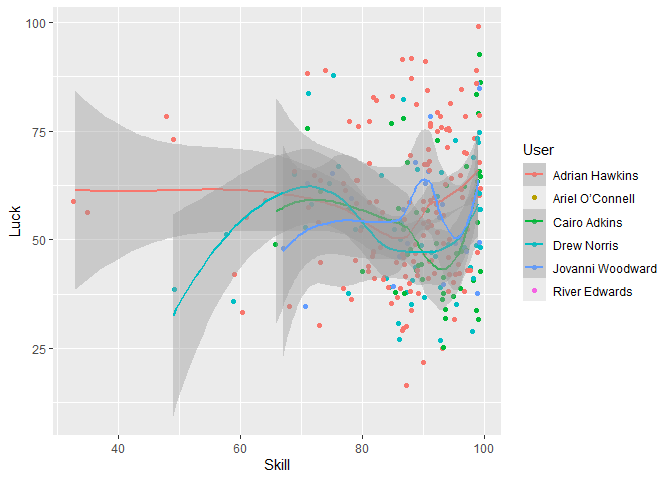
  geom_jitter()

And here’s the same scatter plot with LOESS curves:

wordle %>% ggplot(aes(color = User, x = Skill, y = Luck)) +
  geom_jitter() + 
  geom_smooth(method = 'loess')

Discussion

In this study of 279 Wordle games shared in college friends’ Facebook Messenger group chat, we analyzed each game’s skill and luck scores to assess for an association between those scores and the number of guesses required to solve the puzzle. Our findings challenge conventional wisdom, revealing that high luck scores are more strongly associated with fewer guesses, whereas high skill scores demonstrate a surprisingly weak association with solving efficiency.

Limitations of this work include non-random sampling of Wordle games from a single friend group. Only a minority of games had complete skill, luck, and guess scores, which invites selection bias. Clustering of skill scores between 70 and 99 in our dataset reduces the ability to make inferences about the contribution of low skill scores to the number of guesses needed to solve Wordle. However, the apparent stratification of luck by number of guesses strongly suggests the contribution of luck to solving the puzzle.

The implications of this study reach beyond mere curiosity, offering insights into the nature of problem-solving under uncertainty. In games like Wordle, where initial conditions and guesswork can significantly influence outcomes, our results suggest that chance plays a more pivotal role than traditionally acknowledged. This analysis not only sheds light on the dynamics of Wordle but also prompts a reevaluation of how we understand the balance between luck and skill in similar problem-solving contexts.

Acknowledgements

The introduction and discussion were written with the assistance of generative AI.