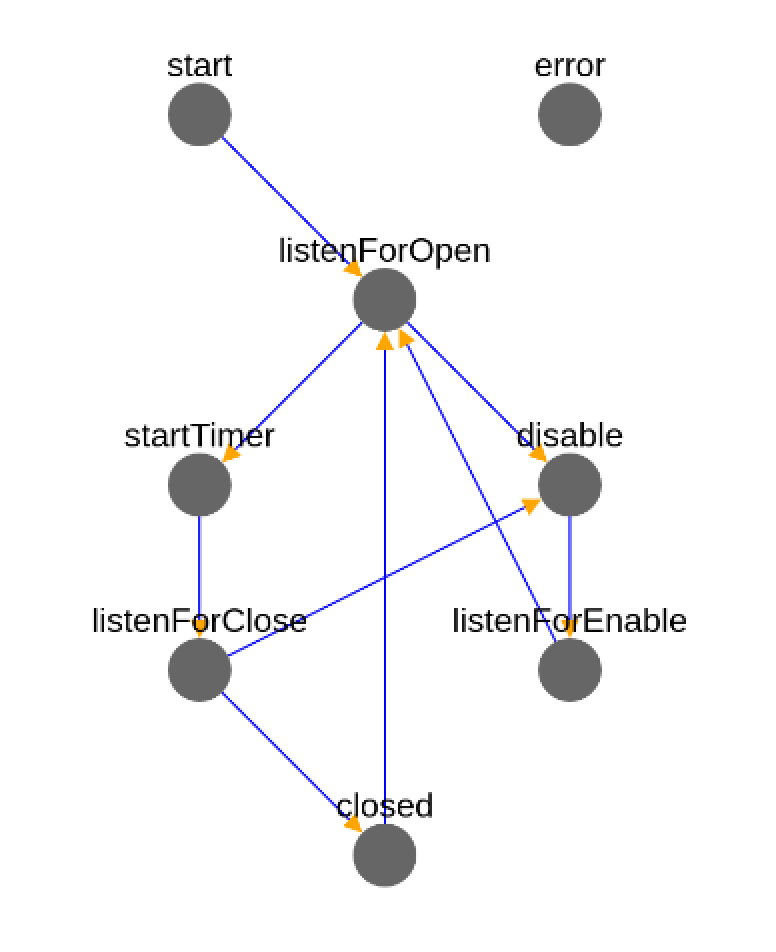
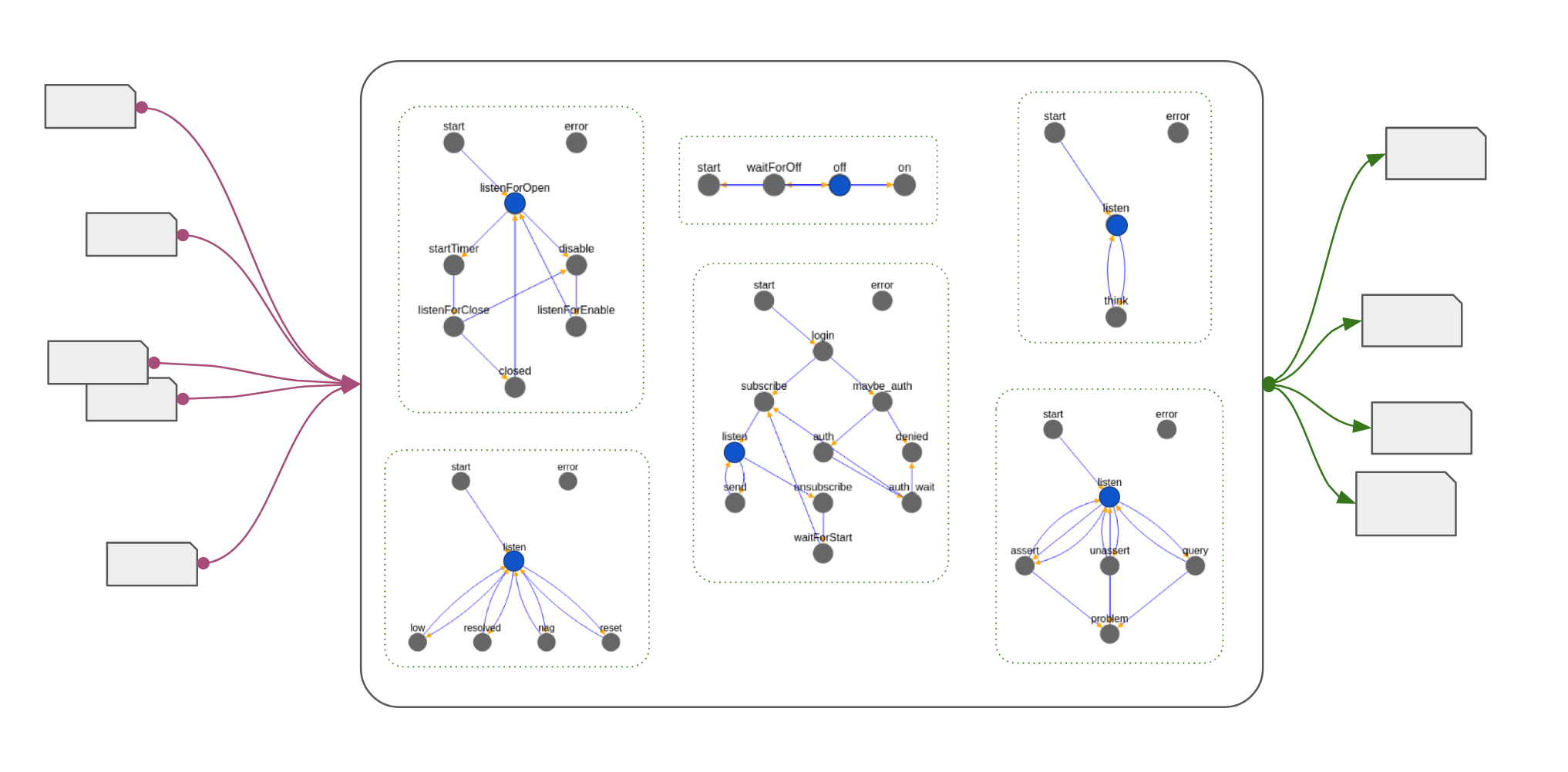
Sheens is an automation engine that hosts message-processing state machines (also called "sheens"). These machines process and emit messages efficiently and atomically. The initial motivation was implementing IoT-oriented home automations; however, Sheens has been useful in other settings.
Sheens is easy to integrate via HTTP, WebSockets, MQTT, plain TCP, Go or C applications, or via other glue. For example, we have integrated Sheens with several internal services, AWS IoT, Home Assistant, and other frameworks.
The structure and behavior of sheens are amenable to standardization, and multiple implementations are feasible and practical. The Sheens engine is highly programmable. Sheen-oriented tools (debuggers, visualizations, monitoring, analyzers) are often easy to implement.
This repo is licensed under Apache License 2.0.
To build, first install Go.
Then:
go get github.com/Comcast/sheens/...
cd $GOPATH/src/github.com/Comcast/sheens # Or equivalent
echo '{"double":1}' | msimple -s specs/double.yaml A bit fancier:
mcrew -s specs -t :9000 &
cat cmd/mcrew/input.txt | nc localhost 9000
kill %%See cmd/mcrew for more discussion, and see the rest of
this README and doc/by-example.md for a start
at documentation.
Applications will all use the core package (which has decent
godoc). If an
application wants a little help with containers of machines, then the
crew package might be a good start. An application should provide
its own message transport (both in and out), and an application should
provide its own persistence. For simple example, see
cmd/msimple, which is a very simple single-machine
process. The example cmd/mcrew demonstrates some
additional functionality.
This project attempts to provide automation gear that is
- Simple
- Robust and correct
- Debuggable, testable
- Efficient
IoT is a motivating application area.
Other objectives
- Pluggable action interpreters. Actions can be written in a language that's executed by pluggable components.
- Transport-agnostic. Input from and output to any sort of messaging services (e.g., HTTP, MQTT, CoAP).
- Pluggable persistence.
- Amenable to formal specification(s) (see below).
- Feasible alternative implementations in other languages.
- Modest resource requirements.
A machine processes and emits messages.
- A machine's state consists of the name of a node and the set of bindings (and a machine specification). A machine's initial bindings are its parameters.
- A machine's specification defines the structure and behavior of the
machine. (See
specsfor some example specifications.) - A state transition is determined by pattern matching against either a pending message or current bindings.
- Actions ideally just generate messages and return new bindings. A good action has no side effects nor will it ever block on IO.
- A collection of machines is called a crew. A crew is typically associated with a user account (or some agent).
- Machines within a crew can send messages to all other machines
in that crew or to a specific machine in that crew.
(Intra-crew messaging is optionally provided by a nanobus via
a pluggable
Router.) - Machines can send messages to any service if routed appropriately.
- Action languages are pluggable. Most examples here are based on goja, which is an ECMAScript implementation.
"Transmit the message to the receiver; hope for an answer some day."
This section provides definitions for machines. For an example-based exposition, see this work-in-progress documentation.
Given a machine specification and some initialization parameters, we can make a machine, which can perform actions in response to messages.
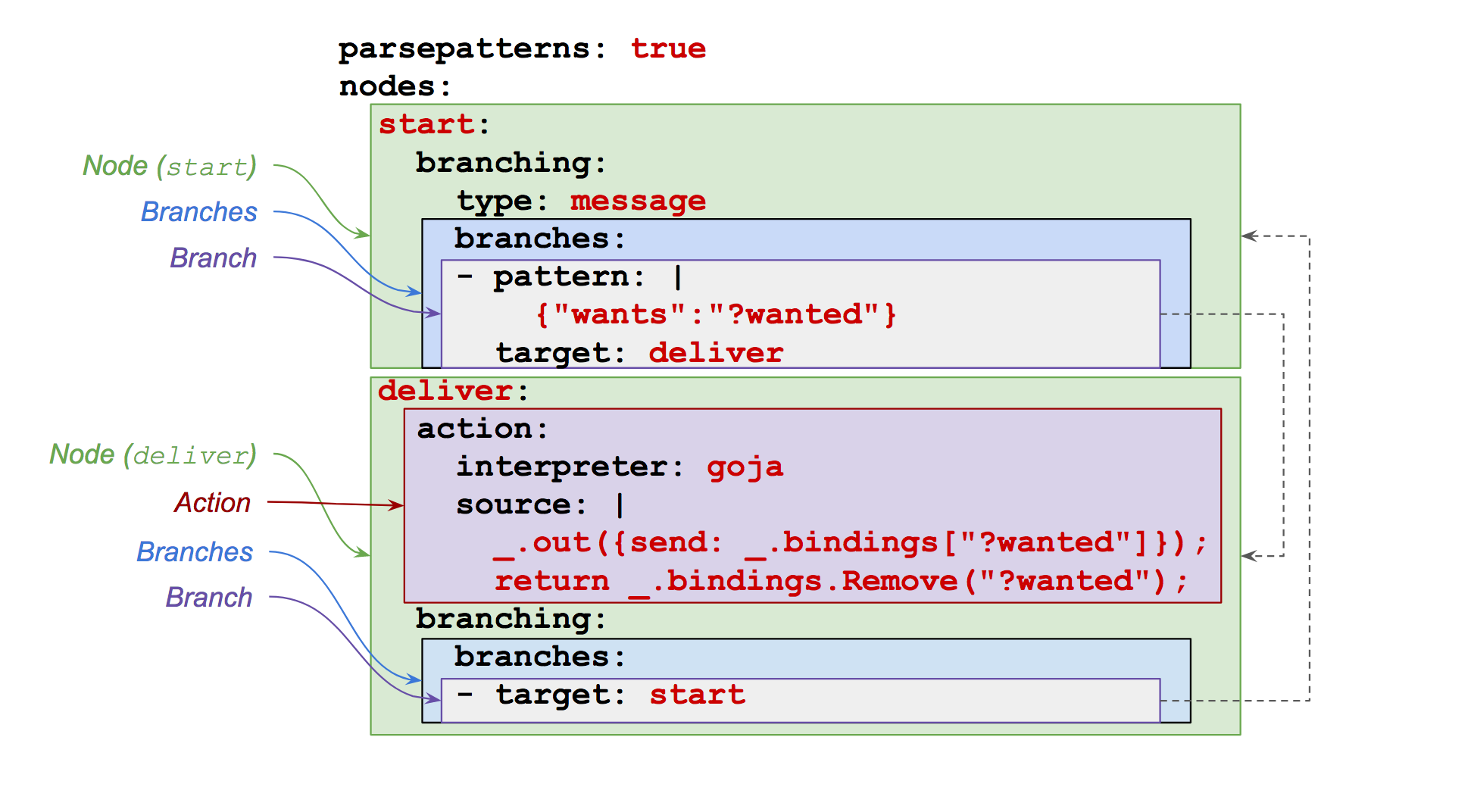
A machine specification consists of a map from node names (just
strings) to nodes. (See specs for some example
specifications.)
A node consists of an optional action and a required branching
specification that consists of a branching type, which is either
message or bindings, and a set of branches to other nodes.
An action could be any function that accepts bindings and returns bindings. Ultimately, an action can (or should) only construct messages and return a new set of bindings. Every action has a timeout, which is enforced.
Each branch consists of an optional pattern, optional guard, and a required target, which is the name of a node in the machine specification.
A pattern is a structure object that can include pattern variables. (See below for more about pattern.) A guard is an optional procedure that generates bindings (perhaps nil) from bindings. If a guard returns no bindings, then the branch isn't followed.
A machine consists of its current state: the name of the current node, the current bindings, and a pointer to the machine's specification. A machine's initial parameters become the machine's first bindings.
A crew is a group of machines associated with some agent.
To try to be happy is to try to build a machine with no other specification than that it shall run noiselessly.
Transitions from one node to another are driven by pattern matching, either against the current set of bindings or a pending message.
A pattern is a map (perhaps with deep structure) that might contain
some strings that start with a ?. Example:
{"person": "homer",
"likes": "?here",
"at": {"type": "residence", "address": "?address"}}A string that starts with a ? is a pattern variable. (The string
? (without anything else) is an anonymous pattern variable that
matches anything and is not based on input bindings or included in
output bindings.)
A message matched against a pattern results in zero or more sets of variable bindings.
As an example, the pattern
{"a":{"b":"?x","c":"?y"},"d":"?y"}matches
{"a":{"b":1,"c":2},"d":2}with a set of bindings
[{"?x":1,"?y":2}]When matching against a message, a map or set (array) value need not be completely specified in the pattern. This behavior is called partial matching. Examples:
Pattern
{"a": 1, "b": "?x"}matches{"a": 1, "b": 2, "c": 3}even though the pattern does not contain a key"c".
Pattern
{"a": 1, "b": ["?x"]}matches{"a": 1, "b": [2,3]}with bindings[{"?x": 2}, {"?x": 3}]. Note the multiple bindings.
With partial matching, backtracking can occur. Also you might get more than one set of bindings.
An array is treated as a set, which can also trigger backtracking. For example, the pattern
{"a":[{"b":"?x"}]}matches
{"a":[{"b":1},{"b":2},{"c":3}]}with the bindings
[{"?x":1},{"?x":2}]For some more examples, see match/match.md, which is
generated by test cases.
The utility patmatch is handy for testing patterns:
patmatch -p '{"a":[{"b":"?x"}]}' -m '{"a":[{"b":1},{"b":2},{"c":3}]}'
[{"?x":1},{"?x":2}]If a pattern variable starts with ??, that variable (or its
associated property when in a map) is optional. Examples:
patmatch -p '{"x":"??opt","y":"?y"}' -m '{"y":"Y"}'
[{"?y":"Y"}]
patmatch -p '{"x":"??opt","y":"?y"}' -m '{"y":"Y","x":"X"}'
[{"??opt":"X","?y":"Y"}]
patmatch -p '["??maybe","a","b"]' -m '["a","b","c"]'
[{"??maybe":"c"}]
patmatch -p '["??maybe","a","b"]' -m '["a","b"]'
[{}]
patmatch -p '["??maybe","a","b"]' -m '["a"]'
nullAs an experimental feature, pattern matching supports numeric inequalities.
The input bindings should include a binding for a variable with a name
that contains either <, >, <=, >=, or != immediately after
the leading ?. The input pattern can then use that variable. When
matching, a value X will match that variable only if the binding Y
for that variable satisfies the inequality with X and Y (in that
order). In this case, the output bindings will include a new binding
for a variable with the same name as the inequality variable but
without the actual inequality.
(Yes, such a feature makes us stare down a slippery slope.)
For example, given input bindings {"?<n":10}, pattern
{"n":"?<n"}, and message {"n":3}, the match will succeed
with bindings {"?<n":10,"?n":3}.
See the matching examples for several examples. (Search for "inequality".)
A machine processes an input message by
-
Obtaining the machine's current node based on the current node name and machine specification.
-
If the current node has branching of type
message, then the message is matched against each branch's pattern. When there's a match, the branch's guard (if any) is executed based on the bindings that resulted from the match. If the guard returns non-nil bindings, the machine's current node name is set to the branch's target, and the machine's current bindings is set to those (non-nil) bindings. When a branch doesn't have a guard, the machine proceeds directly to the branch target.Branches are processed in the order given.
-
If the current node has branching of type
bindings, then the procedure above is executed except that the current bindings are used in place of the input message. The process is execute until the branching are of typemessage, at which point the procedure above is executed.
When the machine arrives at a node that has an action, that action is executed. Action execution results in a new set of bindings, which will replace the current bindings. (An action is given the current bindings.)
A node with an action must have branching of type "bindings", so processing can immediately proceed to the node's branches. (This behavior allows an action to have side effects, but we'd rather actions not have side effects.)
Ideally, actions can only emit messages. In particular, in typical use, an action can't even make an HTTP request!
(You might not have noticed that pattern matching during branch evaluation can result in multiple sets of bindings ("bindingss"). What to do in that case? One approach: If match results in more than one set of bindings, each extra set of bindings results in the creation of a new machine! Alternately: Try each set of bindings in (the arbitrary) order, and go with the first set of bindings that works. That's what the current implementations do, I think.
Retry-like functionality is specified just as any other control flow is specified. There are almost no exceptions. (The only exception is when an internal error occurs, and, even in that case, a setting controls what happens next.
For example, the processor inject the error in bindings to allow for standard, branching-based transitions based on the error. Alternative, the machine could automatically transition to an error node. (That behavior would be the only possibility if the error occured at a location that prevented branching-based error handling.)
A machine's state is independent from other machines' states. Machines can run concurrently without any locking or synchronization.
A machine operates sequentially. Therefore, there are no concurrent state mutations (within a single process).
Virtuous actions have no side effects, and their processing is atomic. Such an action can generate multiple outbound messages, but the processor would only send that batch on if the action terminated without error. Using this behavior, an application can process a message using multiple machines and that entire processing can be atomic.
(Since action interpreters are pluggable, a system can of course provide dangerous action interpreters, which can allow actions to do IO and other unholy things. Yes, you could have a Bash-based action interpreter.)
A virtuous machine action does not block on IO. Therefore machine performance and resource consumption is can be relatively predictable.
(Again, since action interpreters are pluggable, a system can of course provide dangerous action interpreters, which can allow actions to do IO and other unholy things.)
When a message is presented to a set of machines (which could contain
hundreds of machines), we'll want efficient dispatch to the subset of
machines that are waiting on message branching that will (likely)
match the message. Efficient dispatch will likely require an index;
util/index.go heads that direction. Other approaches are of course
possible.
Machines are amenable to debugging using machine-oriented debugging tools that provide the usual operations: reset state, step through transitions, back up, set breakpoints, etc.
Since messages are message processors with exposed state, test tools
(see cmd/mexpect for an example) are relatively easy
to write. The core can be programmed functionality. (There is no
"state" in core!)
If you want to update a machine specification (in a way that's
backward-compatible), you don't have to touch any user data.
Therefore, you can give many machines a new specification with a
single atomic swap (within a process). See core.Specter.
A system could have multiple timer services for different qualities of timers. For example, a nanocron could implement timers with goroutines (with various suitable limits). An external timer service could provide durable timers. Etc.
Though you can happily use sheens without worrying about formalities, you can get formal with sheens if you want to.
The operation of a machine is amenable to formal specification (of evolving precision) and alternate implementations. An interprising investigator could implement a sheens system and prove properties about it. We've started an experiment with Idris along these lines.
In the implementation in this repo, the interpreters for actions and guards are pluggable, so an application is free to provide its own interpreter(s). For example, a conventional native code sheens system, which ideally has been subject to extensive testing, could offer an action interpreter that enables and/or requires proofs of useful properties, such as being total, not making undesired bindings, or only emitting messages with certain properties.
A sheen is not in general a finite state machine. Techincally speaking, a machine is triple of node id, current bindings, and the machine's specification, and the space of bindings is in general not finite. Therefore even holding the specification constant doesn't give a finite state. However, a sheen step does have the Markov property, which makes a wide range of analysis feasible.
For example, consider the projection of a sheen's state space to just the set of nodes defined in the sheens's specification. We now have a finite set of states. Of course, state transitions still have that Markov property. So we can (say) build and maintain simple models of state transition counts over time: count(FROM,TO) → N. If there are S nodes, then that information can be represented as a vector of S*S integer components. Assume we update that data virtually at some interval to reflect a state not changing during that interval. (Of course, we can perform that computation in one go rather than performing some actual heartbeat-like activity.) We could then accumulate a distribution of those vectors over time. Finally, to finish this little example, we could watch for a 2σ (or whatever) excursion, which perhaps indicates a new regime or anomaly of some sort.
As we mentioned above, a virtuous action performs no I/O. Therefore, a single message (or even a batch of messages) can be processed atomically againts a set of machines. In general, the result is a structure that contains new states, which can include error states or conditions, and a set of sequences (of sequences) of messages. The caller can then decide what to do next. If the processing resulted in no system-level error conditions, then all states are updated (hopefully atomically via the application's persistence system). Only then are the output messages actually forwarded to a system that can deliver them (with the required policies/guaranties). If any system-level error condition occured, the application could retry all processing. More economically, the application could retry only the specific failure. Either way, the application need not fear side effects from the previous attempt. Of course, other approaches are possible.
| KING LEAR | How now! what art thou? |
| SHEEN | A machine, sir. |
| KING LEAR | What dost thou profess? what wouldst thou with us? |
| SHEEN | I do profess to be no less than I seem; to serve him truly that will put me in trust: to love him that is honest; to converse with him that is wise, and says little; to fear judgment; to fight when I cannot choose; and to eat no fish. |
| KING LEAR | What art thou? |
| SHEEN | A very honest-hearted machine, and as poor as the king. |
| KING LEAR | If thou be as poor for a subject as he is for a king, thou art poor enough. What wouldst thou? |
| SHEEN | Service. |
| KING LEAR | Who wouldst thou serve? |
| SHEEN | You. |
| KING LEAR | Dost thou know me, fellow? |
| SHEEN | No, sir; but you have that in your countenance which I would fain call master. |
| KING LEAR | What's that? |
| SHEEN | Authority. |
| KING LEAR | What services canst thou do? |
| SHEEN | I can keep honest counsel, ride, run, mar a curious tale in telling it, and deliver a plain message bluntly: that which ordinary men are fit for, I am qualified in; and the best of me is diligence. |
We take our code of conduct seriously. Please abide by it.
Please read our contributing guide for details on how to contribute to our project.
- The Actor Model
- Guards in OCaml
- AWS Step Functions and their state language
- Erlang's
gen_statem - Leslie Lamport on state machines
- The Rulio rules engine
- Little Sheens