The beta measure was introduced by the renowned capital asset pricing model (CAPM) of Sharpe (1964) and Lintner (1965). It relates the expected returns of a security to the market portfolio returns. The resulting measure is the sensitivity of the security returns to changes in the market portfolio returns. The traditional estimation method uses ordinary least squares (OLS) for estimating a linear regression of security excess returns against market excess returns, resulting in an unconditional beta coefficient. The economic intuition behind the CAPM is attractive and easily understood, but Fama and French (2004) showcase poor empirical performance of the model compared to the expectations of the theoretical framework.
More advanced estimation methods accounting for heteroscedasticity, volatility-clustering and time-dependency exist, e.g. GARCH-based models.
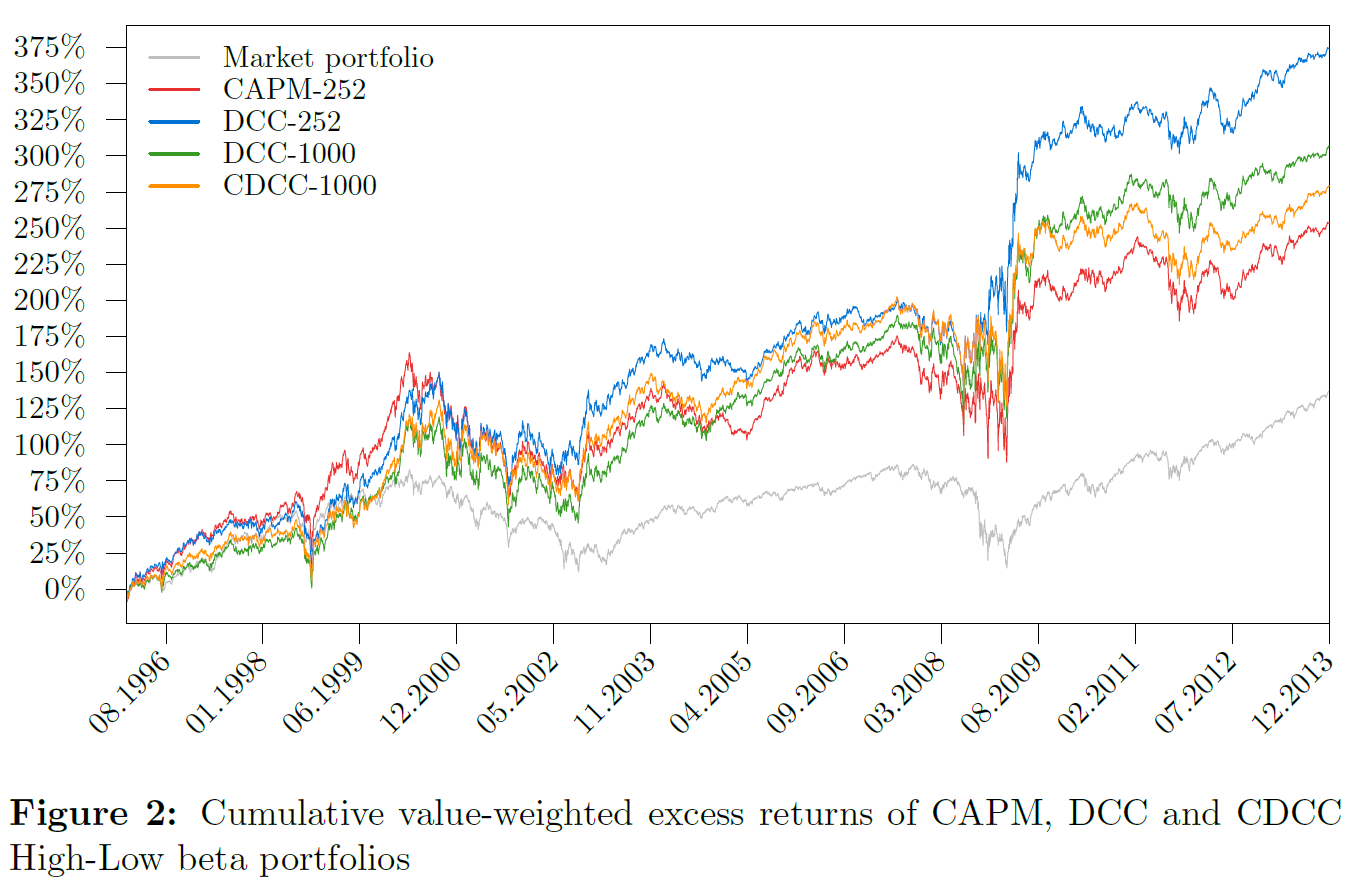
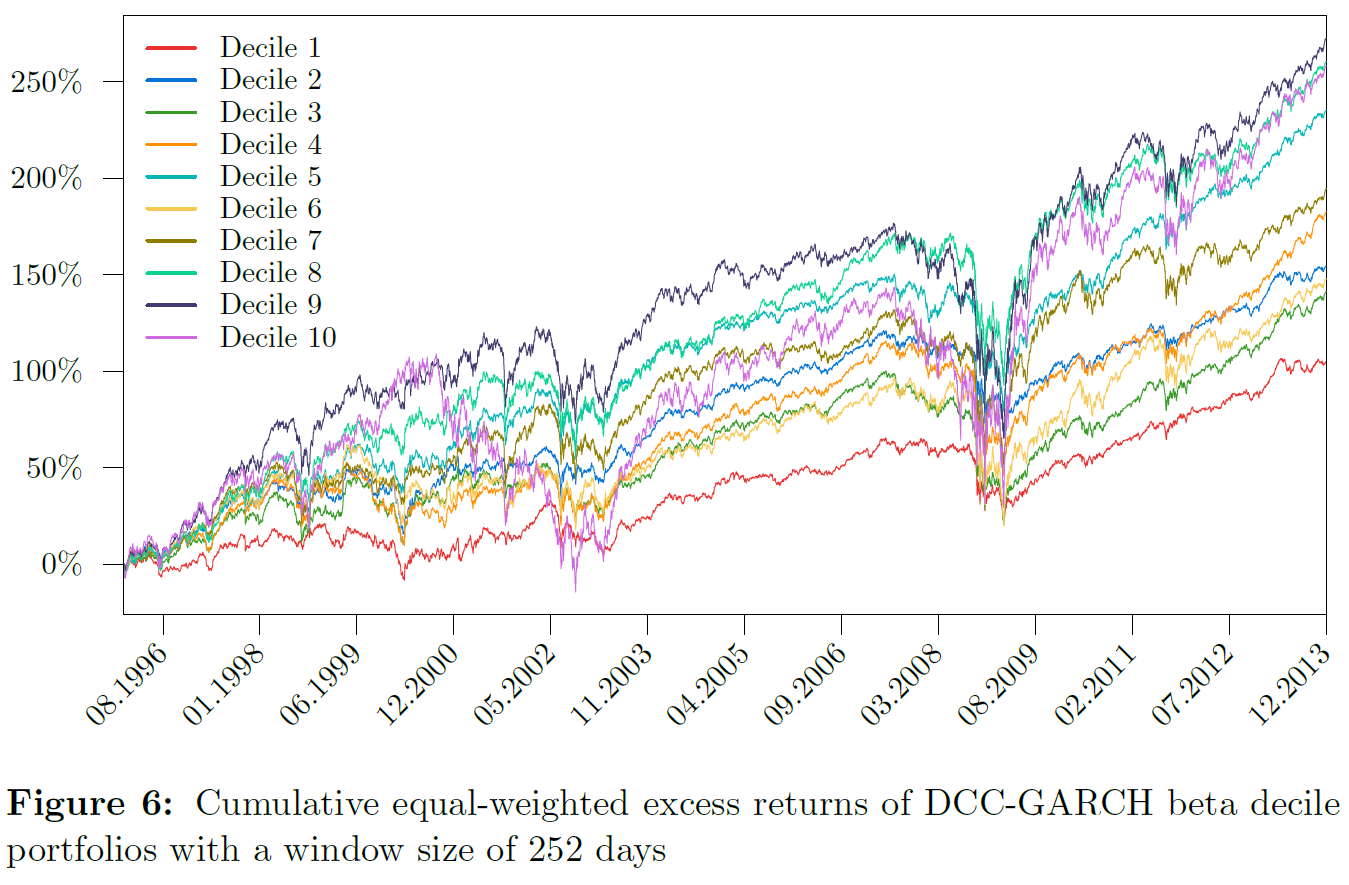
A time-varying conditional beta measure using a DCC-GARCH construct is estimated in Bali, Engle and Tang (2016). It is supposed to have a significant positive relation to the cross-section of daily stock returns. A market neutral investment strategy taking a long position in stocks of the highest conditional beta decile and a short position in stocks of the lowest conditional beta decile yields alphas in the range of 0.60% to 0.80% per month; 0.25% to 0.48% per month by incorporating daily transaction costs.
Paolella and Polak (2015) developed the more realistic, statistically advanced COMFORT model. It utilizes a flexible fat-tailed distribution and combines univariate GARCH-type dynamics with a relatively simple, yet flexible, stochastic volatility dynamic structure. The resulting hybrid GARCH-SV model is able to capture stochastic (co-)jumps in the volatility series and across assets.
This thesis replicates the results obtained by Bali, Engle and Tang (2016) using their Gaussian DCC-GARCH construct on daily stock returns data, with a focus on the market neutral investment strategy results. Subsequently, the DCC-GARCH filter is replaced with the COMFORT model, with the hope and expectation of more significant beta estimations, resulting in a significantly better performance of the investment strategy, namely lower risk with equal or even higher returns
Bali, Turan G. and Engle, Robert F. and Tang, Yi (2016). Dynamic Conditional Beta is Alive and Well in the Cross-Section of Daily Stock Returns. Management Science. 1-20.
Lintner, J. (1965). The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets. The Review of Economics and Statistics, 47(1), 13-37.
Paolella, M. S. and Polak, P. (2015). COMFORT: A common market factor non-gaussian returns model. Journal of Econometrics, 187(2), 593 - 605.
Sharpe, W. (1964). Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. The Journal of Finance, 19(3), 425-442.