fincomepy

A set of tools to perform fixed income securities related calculation in Python. The Python module is accompanied by a Flask app with the same functionality.

Products covered:

Z-spread calculation from zero coupon bond
Z-spread calculation from par coupon bond
Bond price, yield and other related calculations
Repo start payment, end payment, and break even yield
Bond future's net basis and implied repo rate
CDS spread

Author

Xu Ren (xuren2120@gmail.com)

Installation

In the command line:

make install

pip install .

Flask App

To run the app, in the command line:

make run

python app/main.py

Then type

http://127.0.0.1:5000/

in the browser will bring you to the app.

Usage

First import packages

import numpy as np
import matplotlib.pyplot as plt
from datetime import date
from fincomepy import Bond, Repo, BondFuture, ZspreadPar, ZspreadZero, CDS

Z-spread calculation from zero coupon bond

Assuing we have a 5-year bond with 3% annual coupon. Suppose the 1-5 year zero-coupon rates are 1%, 1.5038%, 1.8085%, 2.0652% and 2.2199% respectively. i.e.

Maturity	Zero Coupon Rate	Coupon Cash Flow
1	1.0%	3.0%
2	1.5038%	3.0%
3	1.8085%	3.0%
4	2.0652%	3.0%
5	2.2199%	103.0%

To calculate z-spread, first construct a ZspreadZero object:

zero_discrete = np.array([1.0, 1.5038, 1.8085, 2.0652, 2.2199])
coupon_cf = np.array([3.0, 3.0, 3.0, 3.0, 103.0])
zspr_test1 = ZspreadZero(zero_discrete, coupon_cf)

Obtain z-spread (the value returned is in percentage):

zspr_test1.get_zspread()

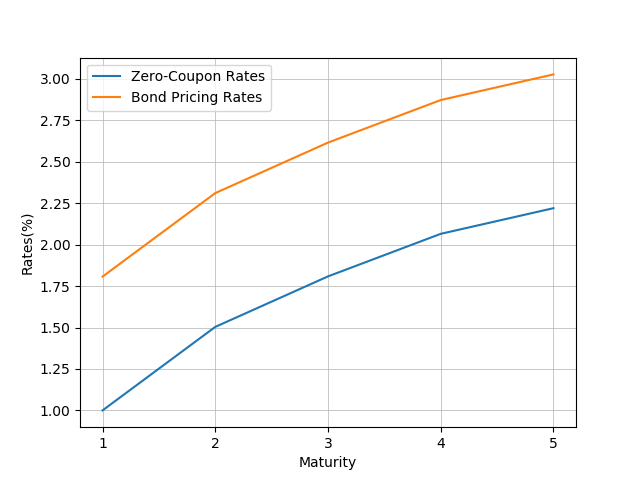
Visualize the z-spread:

zspr_test1.plot_zspread()
plt.show()

Z-spread calculation from par coupon bond

Assuing we have a 5-year bond with 3% annual coupon. Suppose the 1-5 year par-coupon rates are 1%, 1.5%, 1.8%, 2.05%, and 2.2% respectively. i.e.

Maturity	Par Coupon Rate	Coupon Cash Flow
1	1.0%	3.0%
2	1.5%	3.0%
3	1.8%	3.0%
4	2.05%	3.0%
5	2.2%	103.0%

Obtain z-spread (the value returned is in percentage):

par_rates = np.array([1.00, 1.50, 1.80, 2.05, 2.20])
zspr_test2 = ZspreadPar(par_rates, coupon_cf)
zspr_test2.get_zspread()

Bond price, yield and other related calculations

Suppose we have a bond with following information.

	Bond Info
Settlement	2020-7-15
Maturity	2030-5-15
Coupon	0.625%
Market Price	100.015625%
Coupon Frequency	2
Basis	1

Previous coupon payment date (EXCEL equivalent of COUPPCD):

pcd = Bond.couppcd(settlement=date(2020,7,15), maturity=date(2030,5,15), frequency=2, basis=1)
print(pcd)

The "basis" argument specifies the day count convention

Basis	Day Count
0	30/360
1	actual/actual
2	actual/360
3	actual/365
4	30E/360

Next coupon payment date (EXCEL equivalent of COUPNCD):

ncd = Bond.coupncd(settlement=date(2020,7,15), maturity=date(2030,5,15), frequency=2, basis=1)
print(ncd)

Accrued interest (EXCEL equivalent of ACCRINT)

accrued_int = Bond.accrint(issue=pcd, first_interest=ncd, 
   settlement=date(2020,7,15), rate=0.625, par=1, frequency=2, basis=1)
print(accrued_int)

Bond dirty price (EXCEL equivalent of PRICE)

# Given bond yield, calculate bond dirty price. Assuming yield is 0.6233%
dirty_price = Bond.dirty_price(settlement=date(2020,7,15), maturity=date(2030,5,15),
      rate=0.625, yld=0.6233, redemption=100, frequency=2, basis=1)
print(dirty_price)

Bond yield (EXCEL equivalent of YIELD)

yld = Bond.yld(settlement=date(2020,7,15), maturity=date(2030,5,15), rate=0.625,
   pr=100.015625, redemption=100, frequency=2, basis=1)
print(yld)

Bond Macaulay duration, modified duration, DV01 and convexity

# first construct a Bond object
bond_test = Bond(settlement=date(2020,7,15), maturity=date(2030,5,15),
   coupon_perc=0.625, price_perc=100.015625, frequency=2, basis=1)

# Macaulay duration
bond_test.mac_duration()

# modified duration
bond_test.mod_duration()

# DV01
bond_test.DV01()

# convexity
bond_test.convexity()

Estimate bond price change with respect to yield change

# For 0.1% change in yield, the bond price will change by:    
bond_test.price_change(yld_change_perc=0.1)

Repo start payment, end payment, and break even yield

Suppose we have a bond and repo with following information.

	Repo and Bond Info
Settlement	2020-7-15
Maturity	2030-5-15
Coupon	0.625%
Market Price	99.9375%
Coupon Frequency	2
Basis	1
Face Value	$100,000,000
Repo Period	1
Repo Rate	0.145%

Repo purchase price

# first construct a repo object
repo_test = Repo(settlement=date(2020,7,15), maturity=date(2030,5,15), 
   coupon_perc=0.625, price_perc=(99+30/32), frequency=2, basis=1, 
   bond_face_value=100000000, repo_period=1, repo_rate_perc=0.145)
# another way to construct a repo object is to use repo end date
repo_test2 = Repo.from_end_date(settlement=date(2020,7,15), maturity=date(2030,5,15),
   coupon_perc=0.625, price_perc=(99+30/32), frequency=2, basis=1, 
   bond_face_value=100000000, repo_end_date=date(2020,7,16), repo_rate_perc=0.145)

# purchase price without margin or haircut
repo_test.start_payment()
# purchase price with margin
repo_test.purchase_pr_with_margin(margin_perc=102)
# purchase price with haircut
repo_test.purchase_pr_with_haircut(haircut_perc=2)

Repo end payment

repo_test.end_payment()

The Repo purchase and end payment can also be obtained by providing only partial bond information.

# purchase payment
start_payment = Repo.get_start_payment(bond_face_value=100000000, dirty_price_perc=100.06)
print(start_payment)
# end payment
end_payment = Repo.get_end_payment(bond_face_value=100000000, dirty_price_perc=100.06,
   repo_period=32, repo_rate_perc=0.145, type='US')
print(end_payment)

Break even yield

repo_test.break_even_yld()

Bond future's net basis and implied repo rate

Suppose we have the following bond future information.

	Bond Future Info
Settlement	2020-7-17
Maturity	2027-5-15
Coupon	2.375%
Market Price	113.015625%
Coupon Frequency	2
Basis	1
Repo Period	75
Repo Rate	0.14%
Future Price	139.4375%
Conversion Factor	0.8072

# first construct a bond future object
bf_test = BondFuture(settlement=date(2020,7,15), maturity=date(2030,5,15), coupon_perc=0.625, 
   price_perc=99.9375, frequency=2, basis=1, repo_period=30, repo_rate_perc=0.145, 
   futures_pr_perc=140, conversion_factor=0.8)
# similar to repo, another way to construct a bond future object is to use repo end date
# BondFuture.from_end_date()

Forward price

bf_test.forward_price()

Future value

bf_test.full_future_val()

Net basis

bf_test.net_basis()

Implied repo rate

bf_test.implied_repo_rate()

CDS spread

Assuing we have 1-10 years risk free bond rate of 3.12% and 1-10 years risky bond rate of 3.72%. i.e.

Maturity	Risk Free Rate	Risky Rate
1	3.12%	3.72%
2	3.12%	3.72%
3	3.12%	3.72%
4	3.12%	3.72%
5	3.12%	3.72%
6	3.12%	3.72%
7	3.12%	3.72%
8	3.12%	3.72%
9	3.12%	3.72%
10	3.12%	3.72%

To calculate CDS, first construct a CDS object:

# suppose the recovery rate is 40%
cds_test = CDS(risk_free_perc=np.array([3.12]*10), risky_perc=np.array([3.72]*10), 
   face_value_perc=100, rr_perc=40)

Obtain CDS spread:

cds_test.cds_spread()

An alternative way of constructing CDS object is to risk free rate and bond spread

cds_test2 = CDS.from_bond_spread(risk_free_perc=np.array([3.12]*10), 
   spread_perc=np.array([0.6]*10), face_value_perc=100, rr_perc=40)
cds_test2.cds_spread()

reese3928/fincomepy