Лабораторная работа №3 – Контейнер btree_map

Задача: реализовать ассоциативный массив (контейнер btree_map) на основе B-дерева. Каждый узел дерева должен содержать набор пар ключ-значение. Пользователь должен иметь возможность:

получить значение по ключу,
изменить значение по ключу,
добавить в контейнер новую пару.

Алгоритм B-дерево

B-дерево – это сбалансированное дерево поиска, в котором каждый узел содержит множество ключей и имеет более двух потомков.

Здесь количество ключей в узле и количество его потомков зависит от порядка B-дерева. Каждое B-дерево имеет порядок.

B-дерево порядка $m$ обладает следующими свойствами:

Свойство 1: Глубина всех листьев одинакова.
Свойство 2: Все узлы, кроме корня должны иметь как минимум $(m/2) – 1$ ключей и максимум $m-1$ ключей.
Свойство 3: Все узлы без листьев, кроме корня (т.е. все внутренние узлы), должны иметь минимум $m/2$ потомков.
Свойство 4: Если корень – это узел не содержащий листьев, он должен иметь минимум 2 потомка.
Свойство 5: Узел без листьев с $n-1$ ключами должен иметь $n$ потомков.
Свойство 6: Все ключи в узле должны располагаться в порядке возрастания их значений.

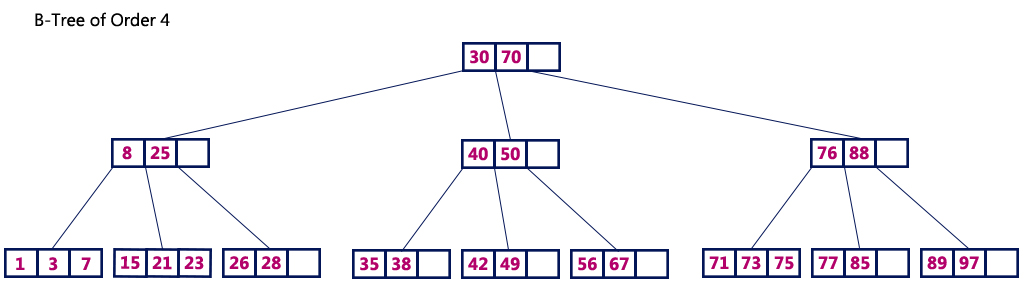
Например, B-дерево 4 порядка содержит максимум 3 значения ключа и максимум 4 потомка для каждого узла.

Операции над B-деревом

Над B-деревом можно проводить следующие операции:

Поиск
Вставка
Удаление

Поиск по B-дереву

Поиск по B-дереву аналогичен поиску по двоичному дереву поиска. В двоичном дереве поиска поиск начинается с корня и каждый раз принимается двустороннее решение (пойти по левому поддереву или по правому). В В-дереве поиск также начинается с корневого узла, но на каждом шаге принимается n-стороннее решение, где $n$ – это общее количество потомков рассматриваемого узла. В В-дереве сложность поиска составляет $O(\log{n})$. Поиск происходит следующим образом:

Шаг 1: Считать элемент для поиска.
Шаг 2: Сравнить искомый элемент с первым значением ключа в корневом узле дерева.
Шаг 3: Если они совпадают, вывести: «Искомый узел найден!» и завершить поиск.
Шаг 4: Если они не совпадают, проверить больше или меньше значение элемента, чем текущее значение ключа.
Шаг 5: Если искомый элемент меньше, продолжить поиск по левому поддереву.
Шаг 6: Если искомый элемент больше, сравнить элемент со следующим значением ключа в узле и повторять Шаги 3, 4, 5 и 6 пока не будет найдено совпадение или пока искомый элемент не будет сравнен с последним значением ключа в узле-листе.
Шаг 7: Если последнее значение ключа в узле-листе не совпало с искомым, вывести «Элемент не найден!» и завершить поиск.

Операция вставки в B-дерево

В В-дереве новый элемент может быть добавлен только в узел-лист. Это значит, что новая пара ключ-значение всегда добавляется только к узлу-листу. Вставка происходит следующим образом:

Шаг 1: Проверить пустое ли дерево.
Шаг 2: Если дерево пустое, создать новый узел с новым значением ключа и его принять за корневой узел.
Шаг 3: Если дерево не пустое, найти подходящий узел-лист, к которому будет добавлено новое значение, используя логику дерева двоичного поиска.
Шаг 4: Если в текущем узле-листе есть незанятая ячейка, добавить новый ключ-значение к текущему узлу-листу, следуя возрастающему порядку значений ключей внутри узла.
Шаг 5: Если текущий узел полон и не имеет свободных ячеек, разделите узел-лист, отправив среднее значение родительскому узлу. Повторяйте шаг, пока отправляемое значение не будет зафиксировано в узле.
Шаг 6: Если разделение происходит с корнем дерева, тогда среднее значение становится новым корнем дерева и высота дерева увеличивается на единицу.

Операция удаления в B-дерево

Удаление ключа из B-дерева еще более громоздкий и сложный процесс, чем вставка. Это связано с тем, что удаление из внутреннего узла требует перестройки дерева в целом. Аналогично вставке необходимо проверять, что мы сохраняем свойства B-дерева, только в данном случае нужно отслеживать, когда ключей $t-1$ (то есть, если из этого узла удалить ключ – то узел не сможет существовать). Удаление происходит следующим образом: