This solution is written in Ruby. It should be enough to have RSpec installed
and run rspec in the top-level directory (here) to see the main test cases;
if needed, a Gemfile is provided, so that one can run bundle to install the
appropriate dependencies.
The solution is the last entry in the spec file, that calls #map and
#reduce on the main class, with the data provided. We find the following
results, rounded to two decimals:
- Duration spent speeding: 11.76s
- Distance covered while speeding: 115.40m
- Total duration: 20s
- Total distance covered: 180.9m
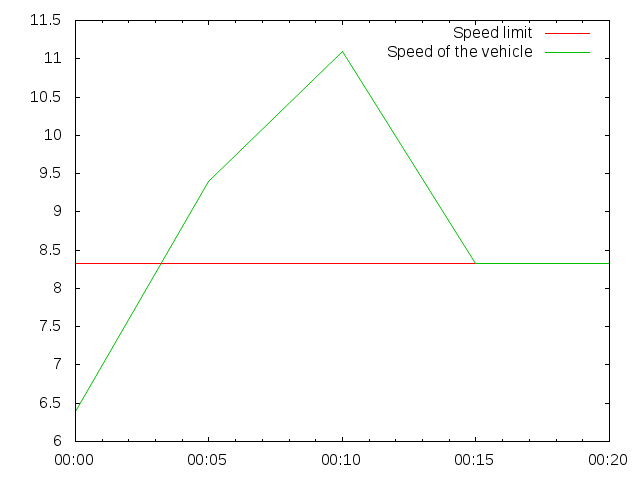
I’ve taken the view that a linear interpolation of the speed between two waypoints provides a sensible model, as the time elapsed between two consecutive waypoints will usually be very short. In this case the interval is 5 seconds, so it certainly fits the expectation. The speed is thus given by this graph:
This is equivalent to saying that the acceleration a is constant between two waypoints. If we denote by s0 and t0 the speed and time at the first waypoint, and s1 and t1 the speed and time at the second one, the acceleration is the slope between these two points:
a = (s1 - s0) / (t1 - t0)
The speed at time t can thus in turn be expressed as
s(t) = ∫t0a dt = a × (t - t0) + s0
or alternatively, using the other waypoint as reference
s(t) = ∫t1a dt = a × (t - t1) + s1
If s0 and s1 are on different sides of the speed limit sℓ, the speed s will reach sℓ at time tℓ such that
s(tℓ) = sℓ ⇔ a × (tℓ - t0) + s0 = sℓ ⇔ tℓ - t0 = (sℓ - s0) / a ⇔ tℓ = t0 + (sℓ - s0) / a
or, using the other waypoint:
tℓ = t1 + (sℓ - s1) / a
This allows us to calculate for how long the driver was over the speed limit (if at all). In the code we use the variable dur to calculate the relative duration rather than absolute times; this is what is interesting to us.
We also want to calculate the distance covered while speeding, this can again be done by integrating:
dist = ∫tℓs(t) dt = ∫tℓ(sℓ + at) dt = sℓ(t - tℓ) + a × (t - tℓ)2 / 2 = (sℓ + a × (t - tℓ) / 2) × (t - tℓ)
and at that point of the code t - tℓ will be assigned to dur, hence
dist = (sℓ + a × dur / 2) × dur
We have a similar formula for the total distance covered (regardless of whether the driver was speeding or not).
The code needs to check that the correct conditions are fulfilled before applying these formulæ, and the tests specify special cases that need to be covered (when acceleration is 0, etc.) One case that is not covered is when the speed limit is different at both waypoints: in this case, the code will return results that are possibly inconsistent. This doesn’t however happen with the data provided.