Nota 1: Esta tarea es colaborativa (en pares y con un repositorio git).
Un medio punto (0.5) se atribuirá en función del buen uso de git entre ambos
participantes (contribuciones equilibradas y revisiones de uno para el otro).
Nota 2: Se atribuirá otro medio punto en la elaboración de tests (por ejemplo con las funciones assert); la idea es que cada uno en el equipo pruebe (con tests) la robustez del código del otro.
En la clase, vimos la estructura de montículo binario. Nos permite, entre otras aplicaciones, implementar de forma eficiente colas de prioridad o ordenar datos. En esta tarea, nos vamos a enfocar en una estructura muy similar, el montículo ternario. Como su nombre lo indica, se trata de una estructura basada en un árbol ternario, en lugar de binario. Significa que cada nodo de este árbol (excepto para los nodos hojas) tiene exactamente tres hijos. Un montículo ternario cumple con las propriedades de los montículos:
-
el árbol ternario correspondiente está casi completo
-
las raíces de cualquier sub-árbol contienen una llave superior a todas las de los otros nodos del sub-árbol.
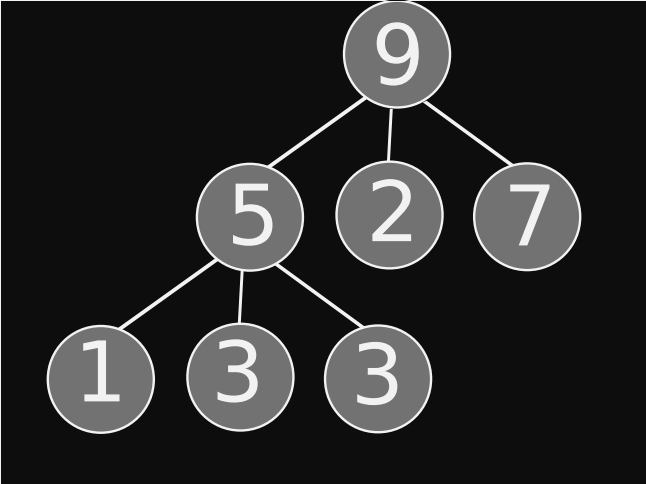
En la figura siguiente, damos un ejemplo de montículo ternario.
Es interesante observar que, de manera similar a lo que vimos en la clase con
montículos binarios, se puede implementar esta estructura con un arreglo,
guardando los datos nivel por nivel. Con el primer dato en el índice 0, se
puede mostrar que los tres hijos del nodo ubicado en el índex k se
encuentran en los índices 3k + 1, 3k + 2, 3k + 3; similarmente, el padre del
nodo de índex k se encuentra en el índex (k − 1)/3.
Para la implementación del montículo ternario, se tomará como modelo la
implementación del montículo binario y se realizará la implementación de la
estructura THeap de las siguientes funciones:
typedef struct _THeap{
//...
}THeap;
THeap * THeap_new(...);
void free_THeap(THeap ** hptr);
void insert(THeap *h, int data);
int removeMax(THeap *h);
int getMax(THeap *h);
void bottomUpHeapify(int *arr, int k);
void topDownHeapify(int * arr, int k, int n);Hacer un análisis de complejidad de los métodos desarrollados (puede venir este análisis como comentario en el código). Comparar en particular el desempeño contra el montículo binario.
// La función reduce se encarga de combinar los elementos de una colección
// aplicando un operador binario, para reducirlos a un solo valor.
//
// ary : [int] -- colección de enteros
// acc : *int -- apuntador al valor de acumulación
// op : ->(int,int){int} -- Operador binario sobre enteros
//
// nil -- al finalizar el apuntador 'acc' tendrá el valor final.
//
// Complejidad O(n*O(op))
// (1) la función itera sobre todo el arreglo
// (2) el operador 'op' es aplicado una vez por cada elemento del arreglo
//
// Si el operador es constante O(1) entonces la complejidad sería O(n).
//
void reduce(array * ary,int * acc,void (*op)(int,int)){
for(int i=0; i < ary->size; i+=1){ // 1
*acc = op(*acc,ary[i]); // 2
}
}En esta aplicación de los montículos, usaremos la estructura desarrollada en la pregunta anterior para determinar el valor mediano de datos llegando como flujo (pensar en datos llegando a través de un medio de comunicación). Cuando el número de datos es impar, tomaremos el único dato que separa el conjunto en dos partes iguales, y cuando es par, tomaremos el promedio de los dos elementos centrales.
Imaginar por ejemplo el flujo siguiente:
1 #=> 1
1 4 #=> 2.5
1 4 6 #=> 4
1 4 6 3 #=> 3Queremos un algoritmo que permita actualizar de manera eficiente el valor mediano, mientras llegan datos nuevos, sin "re-empezar el trabajo" desde cero cada vez, aprovechando que los datos van llegando uno a uno.
Para eso creamos dos montículos: Un montículo-max y un montículo-min.
El primero guardará la mitad inferior de los datos vistos hasta ahora (los
elementos más chicos), mientras el segundo guardará la mitad superior (los
elementos más grandes). Asegurar que la diferencia de tamaño entre los dos
montículos es a lo más uno. Guardar también el valor actual de la mediana
inicializada a 0.
La actualización de la mediana se hará como sigue:
-
montículo_max.size > montículo_min.size: si el nuevo dato leído es inferior al mediano actual, quitar el elemento máximo delmontículo-max, pasarle almontículo-mine insertar el nuevo dato en elmontículo-max; si el nuevo dato es superior al mediano actual, insertarlo en el montículo-min. La mediana es el promedio entre el max y el min. -
montículo_max.size < montículo_min.size: si el nuevo dato leído es superior al mediano actual, quitar el elemento mínimo delmontículo-min, pasarle almontículo-maxe insertar el nuevo dato en elmontículo-min; si el nuevo dato es inferior al mediano actual, insertarlo en elmontículo-max. La mediana es es el promedio entre el max y el min. -
montículo_max.size == montículo_min.size: si el nuevo dato es inferior al mediano actual, ponerlo en el montículo-max y el nuevo mediano será el max; si el nuevo dato es superior al mediano actual, ponerlo en el montículo mín y el nuevo mediano será el min.
Hacer un análisis de complejidad del algoritmo (puede venir este análisis como comentario en el código).
Para la parte colaborativa de la tarea se les pide utilizar la herramienta
git (un sistema de control de versiones) y se les propone utilizar la
plataforma GitHub para coordinar la colaboración. Para
ello necesitan tener la aplicación git, una cuenta en github o ambas.
Se espera lo mínimo en el uso de estas herramientas, esto es:
- push
-
actualizar el repositorio remoto
- branch
-
crear ramas
- checkout
-
cambiar entre ramas
- commit
-
registrar los cambios en el repositorio
- fork
-
crear una copia del repositorio con capacidad de pedir que extraigan e integren el código de nuestra copia.
- pull / pull request
-
extraer de e integrar con otro repositorio o rama.
- merge / merge request
-
combinar dos o más historiales de desarrollo.
En el repositorio git tarea-08 en la plataforma GitHub podrán encontrar este documento con las instrucciones y actualizaciones pertinentes.
Un posible flujo de trabajo que integra las operaciones básicas para la parte colaborativa es el siguiente:
-
crear cuenta en GitHub
-
fork del proyecto por [integrante-1]
-
[integrante-1] invita la colaboración a [integrante-2]
-
crear branch [integrante1-integrante2]
-
cambiar a la nueva rama (branch) [integrante1-integrante2], esta será su rama principal.
-
crear un directorio con nombre [integrante1-integrante2] donde estén todos sus archivos y trabajar en el.
-
crear un issue para coordinar que va a realizar cada quien.
-
crear ramas por bloques de trabajo, por ejemplo se esperaría que al menos tengan las siguientes:
-
implementar-montículo→ asignado a integrante 2 -
tests-montículo→ asignado a integrante 1 -
aplicación-montículo→ asignado a integrante 1 -
test-applicación→ asignado a integrante 2 -
reporte→ asignado a integrante 1 e integrante 2
-
-
hacer pull request en su propio repositorio cuando finalicen el código de una sección a la rama [integrante1-integrante2], por ejemplo
reporte → integrante1-integrante. -
para cada pull request se espera que comenten que realizaron y que el integrante no asignado revise el código antes de hacer merge.
-
una vez tengan finalizada la tarea hacer un pull request al repositorio original (tarea-08)