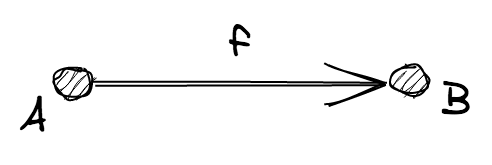Setup
git clone https://github.com/gcanti/functional-programming.git
cd functional-programming
npm iFunctional Programming is programming with pure functions. Mathematical functions.
Una rapida ricerca su internet vi può portare alla seguente definizione:
Una funzione (pura) è una procedura che dato lo stesso input restituisce sempre lo stesso output e non ha alcun side effect osservabile.
Il termine "side effect" non ha ancora un significato preciso (vedremo in seguito come darne una definizione formale), ciò che conta per ora è averne una qualche intuizione, pensate per esempio ad aprire un file per leggerne il contenuto, oppure scrivere su un database.
Per ora possiamo limitarci a dire che un side effect è qualsiasi cosa fa una procedura oltre a restituire un valore.
Ma com'è strutturato un programma che usa solo funzioni pure?
Un programma in stile funzionale tende ad essere scritto come una pipeline:
const program = pipe(
input,
f1, // funzione pura
f2, // funzione pura
f3, // funzione pura
...
)Ciò che accade è che input viene passato come input alla prima funzione f1, la quale restituisce un valore in output che viene passato come input alla seconda funzione f2, la quale restituisce un valore in output che viene passato come input alla terza funzione f3, e così di seguito.
Demo
Vedremo come la programmazione funzionale ci fornisce i mezzi per strutturare il nostro codice in questo stile.
Oltre a capire cosa sia la programmazione funzionale, è altrettanto fondamentale capire quale sia il suo scopo.
L'obbiettivo della programmazione funzionale è dominare la complessità di un sistema usando modelli formali e ponendo particolare attenzione alle proprietà del codice e alla facilità di refactoring.
Functional programming will help teach people the mathematics behind program construction:
- how to write composable code
- how to reason about side effects
- how to write consistent, general, less ad-hoc APIs
Che vuol dire porre attenzione alle proprietà del codice? Vediamo un esempio
Esempio
Perché possiamo dire che la funzione map di Array è "più funzionale" di un ciclo for?
// input
const xs: Array<number> = [1, 2, 3]
// trasformazione
const double = (n: number): number => n * 2
// risultato: voglio un array con tutti gli elementi di `xs` raddoppiati
const ys: Array<number> = []
for (let i = 0; i < xs.length; i++) {
ys.push(double(xs[i]))
}Un ciclo for è molto flessibile, posso modificare:
- l'indice di partenza
- la condizione di fine
- il passo
Ma ciò vuol dire anche che ci sono più possibilità di introdurre errori e non ho alcuna garanzia sul risultato.
Quiz. Avete controllato che io abbia scritto bene il ciclo?
Vediamo ora come si utilizza map
// risultato: voglio un array con tutti gli elementi di `xs` raddoppiati
const ys = xs.map(double)Notate come map sia meno flessibile, tuttavia dà più garanzie:
- gli elementi dell'input verrano processati tutti dal primo all'ultimo
- qualunque sia l'operazione che viene fatta nella callback, il risultato sarà sempre un array con lo stesso numero di elementi dell'array in input
Dal punto di vista funzionale, ambito in cui sono importanti le proprietà del codice piuttosto che i dettagli implementativi, l'operazione map è interessante proprio in quanto limitata.
Pensate per esempio a quanto sia più facile la review di una PR che coinvolga una map rispetto ad un ciclo for.
La programmazione funzionale si appoggia su questi due pilastri:
- trasparenza referenziale
- composizione come design pattern universale
Tutto ciò che vedremo in seguito nel corso deriva direttamente o indirettamente da questi due punti.
Incominciamo dalla trasparenza referenziale.
Definition. An expression is said to be referentially transparent if it can be replaced with its corresponding value without changing the program's behavior
Esempio (la trasparenza referenziale implica l'uso di funzioni pure)
const double = (n: number): number => n * 2
const x = double(2)
const y = double(2)L'espressione double(2) gode della proprietà di trasparenza referenziale perché posso sostituirla con il suo valore 4.
Posso perciò tranquillamente procedere con il seguente refactoring
const x = 4
const y = xNon tutte le espressioni godono della proprietà di trasparenza referenziale, vediamo qualche esempio
Esempio (la trasparenza referenziale implica non lanciare eccezioni)
const inverse = (n: number): number => {
if (n === 0) throw new Error('cannot divide by zero')
return 1 / n
}
const x = inverse(0) + 1Non posso sostituire l'espressione inverse(0) con il suo valore, perciò l'espressione non gode della proprietà di trasparenza referenziale.
Esempio (la trasparenza referenziale può implicare l'utilizzo di strutture dati immutabili)
const xs = [1, 2, 3]
const append = (xs: Array<number>): void => {
xs.push(4)
}
append(xs)
const ys = xsNell'ultima riga non posso sostituire l'espressione xs con il suo valore iniziale [1, 2, 3] dato che il suo valore attuale è stato cambiato dalla chiamata alla funzione append.
Perché è così importante la trasparenza referenziale? Perché permette di:
- ragionare localmente sul codice (ovvero non ho bisogno di conoscere un contesto più ampio per capire un frammento di codice)
- rifattorizzare senza cambiare il comportamento del programma (per la definizione stessa di trasparenza referenziale)
Quiz. Supponiamo di avere il seguente programma:
// In TypeScript `declare` permette di introdurre una definizione senza specificarne l'implementazione.
declare const question: (message: string) => Promise<string>
const x = await question('What is your name?')
const y = await question('What is your name?')Posso rifattorizzarlo in questo modo? Il comportamento del programma è lo stesso o è cambiato?
const x = await question('What is your name?')
const y = xCome potete vedere il refactoring di un programma che contiene espressioni che non godono della proprietà di trasparenza referenziale va affontato con molta cautela. Nella programmazione funzionale, ove ogni espressione gode della proprietà di trasparenza referenziale, il carico cognitivo in fase di refactoring è ridotto.
Parliamo ora del secondo pilastro, la composizione.
Il pattern fondamentale della programmazione funzionale è la componibilità, ovvero la costruzione di piccole unità che fanno qualcosa di specifico in grado di essere combinate tra loro al fine di ottenere entità più grandi e complesse.
Come esempi, e in un percorso dal "più piccolo al più grande", possiamo pensare:
- alla composizione di due semplici valori (come due numeri o due stringhe)
- oppure alla composizione di funzioni
- o anche alla composizione di interi programmi
In questo ultimo caso possiamo parlare di "programmazione modulare":
By modular programming I mean the process of building large programs by gluing together smaller programs - Simon Peyton Jones
Vediamo nella pratica come è possibile tendere verso questo stile di programmazione attraverso l'uso di quelli che vengono chiamati combinatori.
Il termine combinatore si riferisce al combinator pattern:
A style of organizing libraries centered around the idea of combining things. Usually there is some type
T, some "primitive" values of typeT, and some "combinators" which can combine values of typeTin various ways to build up more complex values of typeT
Il concetto di combinatore è piuttosto sfumato e si può presentare in diverse forme, ma la sua forma più semplice è questa:
combinator: Thing -> ThingEsempio. Possiamo pensare alla funzione double come ad un combinatore di numeri.
Lo scopo di un combinatore è quello di creare nuove "cose" da "cose" definite precedentemente.
Notate che il risultato del combinatore può essere nuovamente passato come input, si ottiene perciò una esplosione combinatoria di possibilità, il che rende questo pattern molto potente.
Esempio
import { pipe } from 'fp-ts/function'
const double = (n: number): number => n * 2
console.log(pipe(2, double, double, double)) // => 16Perciò il design generale che potete spesso trovare in un modulo funzionale è questo:
- un modello per
T - un insieme di semplici "primitive" di tipo
T - un insieme di combinatori per combinare le primitive in strutture più complesse
Proviamo ad implementare un modulo di questo tipo:
Demo
Come potete vedere dalla demo precedente, con sole tre primitive e due combinatori siamo stati in grado di esprimere una policy piuttosto complessa.
Pensate a come, aggiungendo anche una sola nuova primitiva (o un nuovo combinatore) a quelli già definiti, le possibilità espressive aumentano esponenzialmente.
Dei due combinatori definiti in 01_retry.ts una menzione speciale va a concat dato che è possibile collegarlo ad una importante astrazione della programmazione funzionale: i semigruppi.
Un semigruppo è una ricetta per combinare due (o più) valori.
Tecnicamente un semigruppo è un'algebra, in generale con il termine "algebra" si intende una particolare combinazione di:
- uno o più insiemi
- una o più operazioni sugli insiemi precedenti
- zero o più leggi a cui devono obbedire le operazioni precedenti
Le algebre sono il modo in cui i matematici catturano un concetto nel modo più diretto eliminando tutto ciò che è superfluo.
Quando si manipola un'algebra sono permesse solo le operazioni definite dall'algebra stessa e in conformità alle sue leggi
L'equivalente delle algebre in programmazione sono le interfacce:
Quando si manipola una interfaccia sono permesse solo le operazioni definite dall'interfaccia stessa e in conformità alle sue leggi.
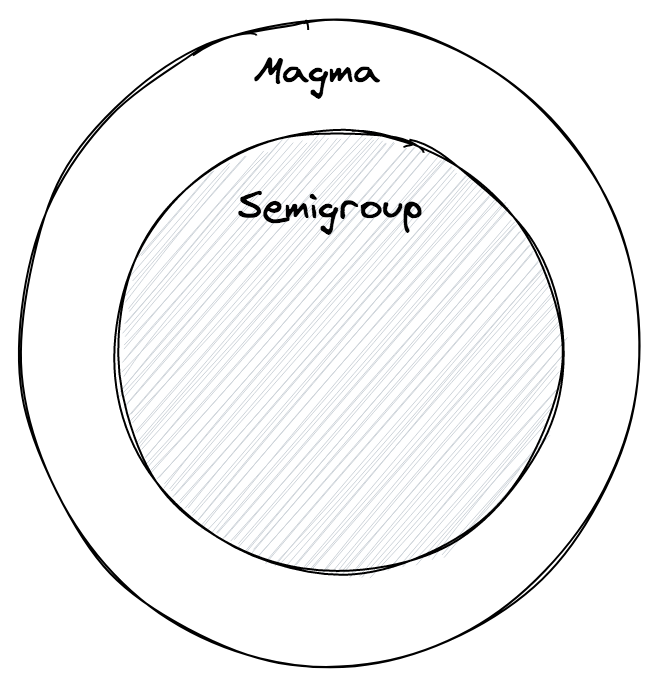
Prima di affrontare i semigruppi vediamo un primo semplice esempio di algebra che li precede: il magma.
Possiamo usare una interface di TypeScript per modellare un magma:
interface Magma<A> {
readonly concat: (first: A, second: A) => A
}Abbiamo quindi un'operazione concat che prende due valori di un certo tipo A e restituisce un nuovo valore dello stesso tipo (proprietà di chiusura). Dato che il risultato può a sua volta essere utilizzato come input l'operazione può essere ripetuta a piacimento. In altre parole concat è un combinatore per il tipo A.
Quiz. Il fatto che una operazione sia chiusa non è una proprietà banale, potete fare un esempio di operazione sui numeri naturali (ovvero i numeri interi positivi) per cui la proprietà di chiusura non vale?
Per avere una istanza concreta di magma per un determinato tipo occorre perciò definire un oggetto conforme a questa interfaccia.
Esempio (una istanza di Magma per il tipo number)
import { Magma } from 'fp-ts/Magma'
const MagmaSub: Magma<number> = {
concat: (first, second) => first - second
}
console.log(
MagmaSub.concat(
MagmaSub.concat(MagmaSub.concat(MagmaSub.concat(10, 2), 3), 1),
2
)
)
// => 2
// helper
const getPipeableConcat = <A>(M: Magma<A>) => (second: A) => (first: A): A =>
M.concat(first, second)
const concat = getPipeableConcat(MagmaSub)
// esempio di utilizzo
import { pipe } from 'fp-ts/function'
pipe(10, concat(2), concat(3), concat(1), concat(2), console.log)
// => 2Notate che la definizione di concat è stata concepita per agevolarne l'uso con pipe.
Quiz. Consideriamo la seguente funzione che trasforma una lista in un dizionario, perché si richiede un Magma come parametro?
import { pipe } from 'fp-ts/function'
import { Magma } from 'fp-ts/Magma'
declare const fromReadonlyArray: <A>(
M: Magma<A>
) => (as: ReadonlyArray<readonly [string, A]>) => Record<string, A>
// esempio di utilizzo
const MagmaSub: Magma<number> = {
concat: (first, second) => first - second
}
pipe(
[
['a', 1],
['b', 2]
],
fromReadonlyArray(MagmaSub),
console.log
) // => { a: 1, b: 2 }
pipe(
[
['a', 1],
['b', 2],
['a', 3]
],
fromReadonlyArray(MagmaSub),
console.log
) // => { a: -2, b: 2 }Un Magma<A> è un'algebra molto semplice:
- un insieme (
A) - una operazione (
concat) - nessuna legge
vediamo ora un'algebra che definisce una legge: i semigruppi.
Se l'operazione concat di un Magma è anche associativa allora parliamo di semigruppo.
Un'operazione binaria * si dice "associativa" se vale:
(x * y) * z = x * (y * z)per ogni x, y, z.
L'associatività ci dice che non dobbiamo preoccuparci delle parentesi nelle espressioni e che, volendo, possiamo scrivere semplicemente x * y * z (non c'è ambiguità).
Esempio
La concatenazione di stringhe (+) gode della proprietà associativa.
("a" + "b") + "c" = "a" + ("b" + "c") = "abc"Ogni semigruppo è un magma, ma non ogni magma è un semigruppo.
Esempio
Il magma MagmaSub che abbiamo visto nella sezione precedente non è un semigruppo poiché la sua operazione concat non è associativa:
import { pipe } from 'fp-ts/function'
import { Magma } from 'fp-ts/Magma'
const MagmaSub: Magma<number> = {
concat: (first, second) => first - second
}
pipe(MagmaSub.concat(MagmaSub.concat(1, 2), 3), console.log) // => -4
pipe(MagmaSub.concat(1, MagmaSub.concat(2, 3)), console.log) // => 2I semigruppi catturano l'essenza delle operazioni parallelizzabili.
Infatti se sappiamo che una data operazione * gode della proprietà associativa possiamo suddividere una computazione in due sotto computazioni, ognuna delle quali può essere ulteriormente suddivisa
a * b * c * d * e * f * g * h = ((a * b) * (c * d)) * ((e * f) * (g * h))Le sotto computazioni possono essere distribuite ed eseguite parallelamente per poi raccoglierne i risultati parziali e comporre il risultato finale.
Come già successo per Magma, i semigruppi possono essere modellati con una interface di TypeScript:
interface Semigroup<A> {
readonly concat: (first: A, second: A) => A
}Come vedete la definizione è identica a quella di Magma ma c'è una differenza importante, deve valere la seguente legge (che purtroppo non può essere codificata nel type system di TypeScript):
Associativity. Se S è un semigruppo deve valere:
S.concat(S.concat(x, y), z) = S.concat(x, S.concat(y, z))per ogni x, y, z in A
Esempio
Implementiamo un semigruppo per ReadonlyArray<string>
import * as Se from 'fp-ts/Semigroup'
const Semigroup: Se.Semigroup<ReadonlyArray<string>> = {
concat: (first, second) => first.concat(second)
}Come potete vedere il nome concat ha particolarmente senso per i ReadonlyArray ma, in base al contesto e al tipo A per il quale stiamo implementando una istanza, l'operazione di semigruppo concat può essere interpretata con diversi significati:
- "concatenare"
- "combinare"
- "merging"
- "fondere"
- "selezionare"
- "sommare"
- "sostituire"
e altri ancora.
Esempio
Ecco come implementare il semigruppo (number, +) dove + è l'usuale addizione di numeri:
import { Semigroup } from 'fp-ts/Semigroup'
/** number `Semigroup` under addition */
const SemigroupSum: Semigroup<number> = {
concat: (first, second) => first + second
}Quiz. Il combinatore concat definito nella demo 01_retry.ts può essere utilizzato per definire una istanza di Semigroup per il tipo RetryPolicy?
Si noti che, fissato un tipo, si possono definire molteplici istanze dell'interfaccia Semigroup.
Per esempio, considerando ancora il tipo number, possiamo definire il semigruppo (number, *) dove * è l'usuale moltiplicazione di numeri:
import { Semigroup } from 'fp-ts/Semigroup'
/** number `Semigroup` under multiplication */
const SemigroupProduct: Semigroup<number> = {
concat: (first, second) => first * second
}Un altro esempio, con le stringhe questa volta:
import { Semigroup } from 'fp-ts/Semigroup'
const SemigroupString: Semigroup<string> = {
concat: (first, second) => first + second
}E ancora altri due esempi, con boolean:
import { Semigroup } from 'fp-ts/Semigroup'
const SemigroupAll: Semigroup<boolean> = {
concat: (first, second) => first && second
}
const SemigroupAny: Semigroup<boolean> = {
concat: (first, second) => first || second
}Per definizione concat combina solo due elementi di A alla volta, è possibile combinare più elementi?
La funzione concatAll prende in input una istanza di semigruppo, un valore iniziale e un array di elementi da combinare:
import * as S from 'fp-ts/Semigroup'
import * as N from 'fp-ts/number'
const sum = S.concatAll(N.SemigroupSum)(2)
console.log(sum([1, 2, 3, 4])) // => 12
const product = S.concatAll(N.SemigroupProduct)(3)
console.log(product([1, 2, 3, 4])) // => 72Quiz. Perché ho bisogno di un valore iniziale?
Esempio
Come altri esempi di applicazione di concatAll, possiamo reimplementare alcune popolari funzioni della standard library di JavaScript:
import * as B from 'fp-ts/boolean'
import { concatAll } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/struct'
const every = <A>(predicate: (a: A) => boolean) => (
as: ReadonlyArray<A>
): boolean => concatAll(B.SemigroupAll)(true)(as.map(predicate))
const some = <A>(predicate: (a: A) => boolean) => (
as: ReadonlyArray<A>
): boolean => concatAll(B.SemigroupAny)(false)(as.map(predicate))
const assign: (as: ReadonlyArray<object>) => object = concatAll(
S.getAssignSemigroup<object>()
)({})Quiz. La seguente istanza è "legale" (ovvero rispetta le leggi dei semigruppi)?
import { Semigroup } from 'fp-ts/Semigroup'
/** Always return the first argument */
const first = <A>(): Semigroup<A> => ({
concat: (first, _second) => first
})Quiz. La seguente istanza è legale?
import { Semigroup } from 'fp-ts/Semigroup'
/** Always return the second argument */
const last = <A>(): Semigroup<A> => ({
concat: (_first, second) => second
})Data una istanza di semigruppo, è possibile ricavarne un'altra semplicemente scambiando l'ordine in cui sono combinati gli elementi:
import { pipe } from 'fp-ts/function'
import { Semigroup } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'
// questo è un combinatore di semigruppi...
const reverse = <A>(S: Semigroup<A>): Semigroup<A> => ({
concat: (first, second) => S.concat(second, first)
})
pipe(S.Semigroup.concat('a', 'b'), console.log) // => 'ab'
pipe(reverse(S.Semigroup).concat('a', 'b'), console.log) // => 'ba'Quiz. Questo combinatore ha senso perché in generale l'operazione concat non è commutativa, ovvero non è detto che valga sempre concat(x, y) = concat(y, x), potete portare un esempio in cui concat non è commutativa? E uno in cui è commutativa?
Proviamo a definire delle istanze di semigruppo per tipi più complessi:
import * as N from 'fp-ts/number'
import { Semigroup } from 'fp-ts/Semigroup'
// modella un vettore che parte dall'origine
type Vector = {
readonly x: number
readonly y: number
}
// modella la somma di due vettori
const SemigroupVector: Semigroup<Vector> = {
concat: (first, second) => ({
x: N.SemigroupSum.concat(first.x, second.x),
y: N.SemigroupSum.concat(first.y, second.y)
})
}Esempio
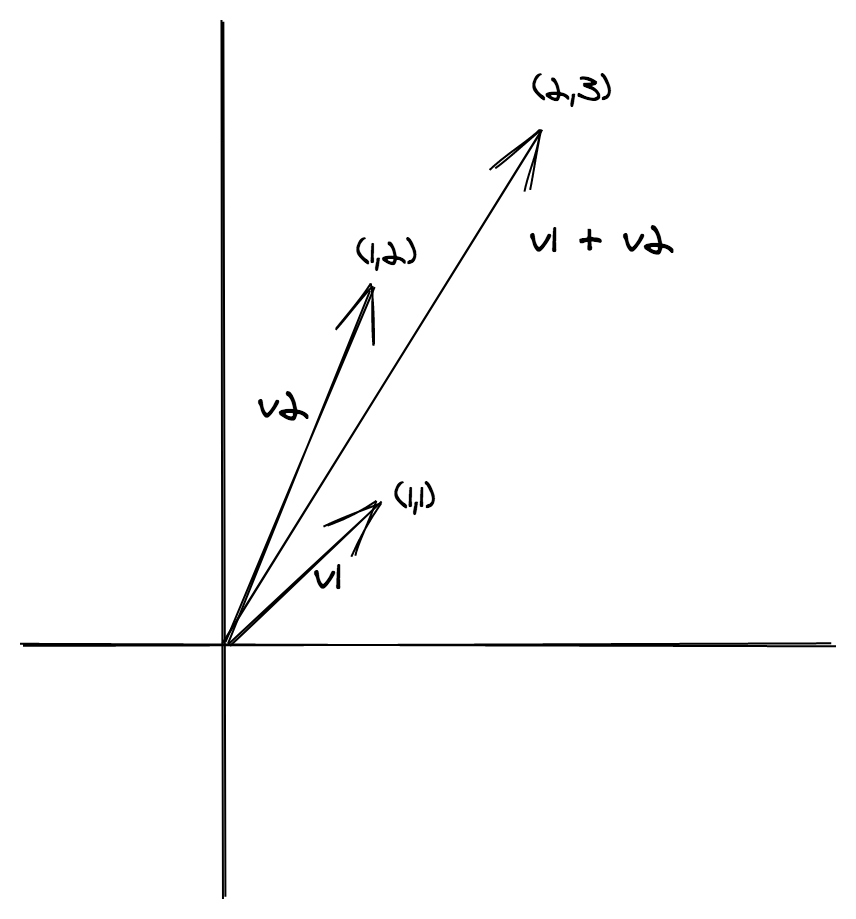
const v1: Vector = { x: 1, y: 1 }
const v2: Vector = { x: 1, y: 2 }
console.log(SemigroupVector.concat(v1, v2)) // => { x: 2, y: 3 }Troppo boilerplate? La buona notizia è che la teoria matematica che sta dietro al concetto di semigruppo ci dice che possiamo costruire una istanza di semigruppo per una struct come Vector se siamo in grado di fornire una istanza di semigruppo per ogni suo campo.
Convenientemente il modulo fp-ts/Semigroup esporta una combinatore struct:
import { struct } from 'fp-ts/Semigroup'
// modella la somma di due vettori
const SemigroupVector: Semigroup<Vector> = struct({
x: N.SemigroupSum,
y: N.SemigroupSum
})Nota. Esiste un combinatore simile a struct ma che lavora con le tuple: tuple
import * as N from 'fp-ts/number'
import { Semigroup, tuple } from 'fp-ts/Semigroup'
// modella un vettore che parte dall'origine
type Vector = readonly [number, number]
// modella la somma di due vettori
const SemigroupVector: Semigroup<Vector> = tuple(N.SemigroupSum, N.SemigroupSum)
const v1: Vector = [1, 1]
const v2: Vector = [1, 2]
console.log(SemigroupVector.concat(v1, v2)) // => [2, 3]Quiz. E' vero che dato un semigruppo per A e scelto un qualsiasi elemento middle di A, se lo infilo tra i due parametri di concat, ottengo ancora un semigruppo?
import { pipe } from 'fp-ts/function'
import { Semigroup } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'
export const intercalate = <A>(middle: A) => (
S: Semigroup<A>
): Semigroup<A> => ({
concat: (first, second) => S.concat(S.concat(first, middle), second)
})
const SemigroupIntercalate = pipe(S.Semigroup, intercalate('|'))
pipe(
SemigroupIntercalate.concat('a', SemigroupIntercalate.concat('b', 'c')),
console.log
) // => 'a|b|c'L'associatività è una proprietà molto forte, cosa accade se, dato un particolare tipo A, non si riesce a trovare una operazione associativa su A?
Supponiamo di avere un tipo User definito come:
type User = {
readonly id: number
readonly name: string
}e che nel mio database ci siano molte copie dello stesso User (per esempio potrebbero essere la storia della sue modifiche)
// API interne
declare const getCurrent: (id: number) => User
declare const getHistory: (id: number) => ReadonlyArray<User>e di dover disegnare una API pubblica
export declare const getUser: (id: number) => Userche tiene conto di tutte le copie in base a qualche criterio, per esempio il criterio potrebbe essere restituire la copia più recente, oppure quella meno recente, oppure sempre la copia corrente, ecc...
Naturalmente possiamo definire delle API specifiche per ogni criterio, dunque:
export declare const getMostRecentUser: (id: number) => User
export declare const getLeastRecentUser: (id: number) => User
export declare const getCurrentUser: (id: number) => User
// ecc...In questa sede però vorrei parlare del problema di design dal punto di vista più generale possibile.
Dunque per restituire un valore di tipo User devo considerare tutte le copie a farne un "merge" (o una "selezione").
In altre parole possiamo modellare il criterio con un semigruppo!
Tuttavia non è evidente cosa voglia dire "fare merge di due utenti", né come questa operazione di merge possa essere associativa.
Potete sempre definire una istanza di semigruppo per un qualsiasi tipo costruendo una istanza di semigruppo non per A ma per ReadonlyNonEmptyArray<A> (array non vuoto di A) chiamata il semigruppo libero di A.
import { Semigroup } from 'fp-ts/Semigroup'
// modella un array non vuoto, ovvero con almeno un elemento
type ReadonlyNonEmptyArray<A> = ReadonlyArray<A> & {
readonly 0: A
}
// la concatenazione di due array non vuoti è ancora un array non vuoto
const getSemigroup = <A>(): Semigroup<ReadonlyNonEmptyArray<A>> => ({
concat: (first, second) => [first[0], ...first.slice(1), ...second]
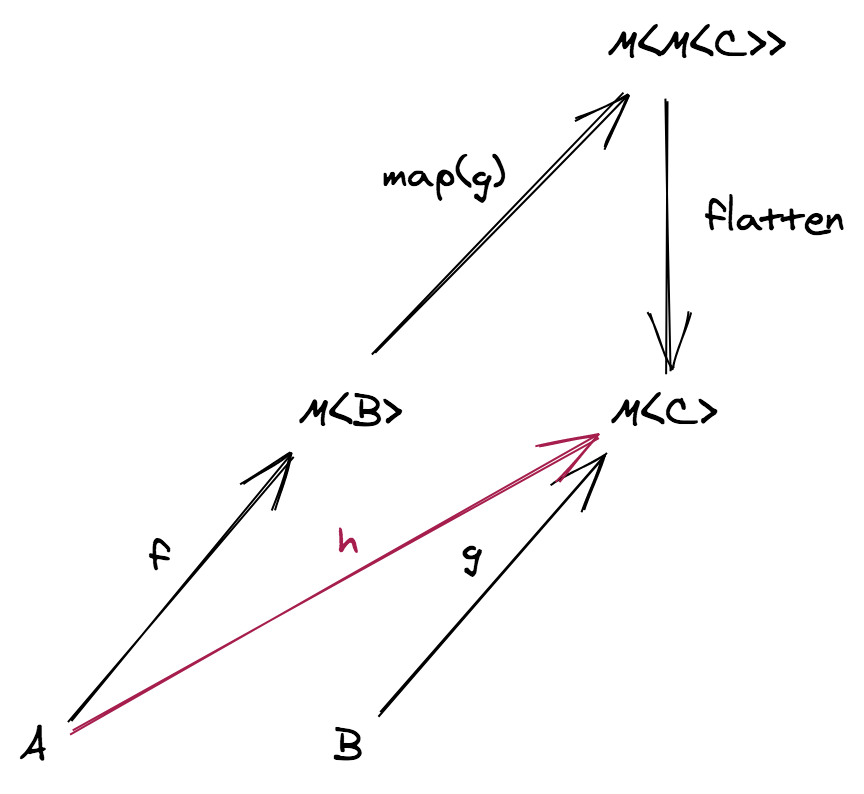
})e poi mappare gli elementi di A ai "singoletti" di ReadonlyNonEmptyArray<A>, ovvero un array con un solo elemento:
// inserisce un valore in un array non vuoto
const of = <A>(a: A): ReadonlyNonEmptyArray<A> => [a]Applichiamo questa tecnica al tipo User:
import {
getSemigroup,
of,
ReadonlyNonEmptyArray
} from 'fp-ts/ReadonlyNonEmptyArray'
import { Semigroup } from 'fp-ts/Semigroup'
type User = {
readonly id: number
readonly name: string
}
// questo è un semigruppo non per `User` ma per `ReadonlyNonEmptyArray<User>`
const S: Semigroup<ReadonlyNonEmptyArray<User>> = getSemigroup<User>()
declare const user1: User
declare const user2: User
declare const user3: User
// const merge: ReadonlyNonEmptyArray<User>
const merge = S.concat(S.concat(of(user1), of(user2)), of(user3))
// ottengo lo stesso risultato "impacchettando a mano" gli utenti
const merge2: ReadonlyNonEmptyArray<User> = [user1, user2, user3]Il semigruppo libero di A quindi non è altro che il semigruppo in cui gli elementi sono tutte le possibili sequenze finite e non vuote di elementi di A.
Il semigruppo libero di A può essere visto come un modo lazy di concatenare elementi di A, mantenendo in tal modo tutto il contenuto informativo.
Infatti il valore merge, che contiene [user1, user2, user3], mi dice ancora quali sono gli elementi da concatenare e in che ordine.
Ora ho tre opzioni possibili in fase di design della API getUser:
- sono in grado di definire un
Semigroup<User>e voglio procedere subito al merging
declare const SemigroupUser: Semigroup<User>
export const getUser = (id: number): User => {
const current = getCurrent(id)
const history = getHistory(id)
// procedo subito al merging
return concatAll(SemigroupUser)(current)(history)
}- non sono in grado di definire un
Semigroup<User>oppure voglio lasciare come configurabile la strategia di merging, perciò la chiedo al consumer della mia API
export const getUser = (SemigroupUser: Semigroup<User>) => (
id: number
): User => {
const current = getCurrent(id)
const history = getHistory(id)
// procedo subito al merging
return concatAll(SemigroupUser)(current)(history)
}- non sono in grado di definire un
Semigroup<User>e non voglio chiederlo al consumer della mia API
Questo è il caso in cui il semigruppo libero di User ci può venire in aiuto.
export const getUser = (id: number): ReadonlyNonEmptyArray<User> => {
const current = getCurrent(id)
const history = getHistory(id)
// decido di NON procedere al merging e restituisco il semigruppo libero di `User`
return [current, ...history]
}Inoltre, anche se ho a disposizione una istanza di semigruppo per A, potrei decidere ugualmente di usare il suo semigruppo libero per i seguenti motivi:
- evita di eseguire computazioni possibilmente inutili (supponete che il merging sia costoso)
- evita di passare in giro l'istanza di semigruppo
- permette ancora al consumer delle mie API di stabilire la strategia di merging (usando
concatAll)
Dato che number è totalmente ordinabile (ovvero dati due qualsiasi numeri x e y, una tra le seguenti condizioni vale: x <= y oppure y <= x) possiamo definire due sue ulteriori istanze di semigruppo usando min e max come operazioni:
import { Semigroup } from 'fp-ts/Semigroup'
const SemigroupMin: Semigroup<number> = {
concat: (first, second) => Math.min(first, second)
}
const SemigroupMax: Semigroup<number> = {
concat: (first, second) => Math.max(first, second)
}Quiz. Perché è importante che number sia totalmente ordinabile?
Sarebbe utile poter definire questi due semigruppi (SemigroupMin e SemigroupMax) anche per altri tipi oltre a number.
È possibile catturare la nozione di totalmente ordinabile per altri tipi? Per farlo dobbiamo prima di tutto catturare la nozione di uguaglianza.
Ancora una volta possiamo modellare la nozione di uguaglianza tramite una interface di TypeScript:
interface Eq<A> {
readonly equals: (first: A, second: A) => boolean
}Intuitivamente:
- se
equals(x, y)è uguale atrueallora diciamo chexeysono uguali - se
equals(x, y)è uguale afalseallora diciamo chexeysono diversi
Esempio
Proviamo a definire una istanza di Eq per il tipo number:
import { Eq } from 'fp-ts/Eq'
import { pipe } from 'fp-ts/function'
const EqNumber: Eq<number> = {
equals: (first, second) => first === second
}
pipe(EqNumber.equals(1, 1), console.log) // => true
pipe(EqNumber.equals(1, 2), console.log) // => falseDevono valere le seguenti leggi:
- Reflexivity:
equals(a, a) === true, per ogniainA - Symmetry:
equals(a, b) === equals(b, a), per ognia,binA - Transitivity: se
equals(a, b) === trueeequals(b, c) === true, alloraequals(a, c) === true, per ognia,b,cinA
Quiz. Ha senso un combinatore reverse: <A>(E: Eq<A>) => Eq<A>?
Quiz. Ha senso un combinatore not: <A>(E: Eq<A>) => Eq<A>?
import { Eq } from 'fp-ts/Eq'
export const not = <A>(E: Eq<A>): Eq<A> => ({
equals: (first, second) => !E.equals(first, second)
})Esempio
Come primo esempio di utilizzo dell'astrazione Eq definiamo una funzione elem che indica se un dato valore è un elemento di un ReadonlyArray:
import { Eq } from 'fp-ts/Eq'
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
// restituisce `true` se l'elemento `a` compare nella lista `as`
const elem = <A>(E: Eq<A>) => (a: A) => (as: ReadonlyArray<A>): boolean =>
as.some((e) => E.equals(a, e))
pipe([1, 2, 3], elem(N.Eq)(2), console.log) // => true
pipe([1, 2, 3], elem(N.Eq)(4), console.log) // => falseMa perché non usare il metodo nativo includes degli array?
console.log([1, 2, 3].includes(2)) // => true
console.log([1, 2, 3].includes(4)) // => falsePer avere una risposta proviamo a definire una istanza per un tipo più complesso:
import { Eq } from 'fp-ts/Eq'
type Point = {
readonly x: number
readonly y: number
}
const EqPoint: Eq<Point> = {
equals: (first, second) => first.x === second.x && first.y === second.y
}
console.log(EqPoint.equals({ x: 1, y: 2 }, { x: 1, y: 2 })) // => true
console.log(EqPoint.equals({ x: 1, y: 2 }, { x: 1, y: -2 })) // => falsee utilizzare fianco a fianco elem e includes
const points: ReadonlyArray<Point> = [
{ x: 0, y: 0 },
{ x: 1, y: 1 },
{ x: 2, y: 2 }
]
const search: Point = { x: 1, y: 1 }
console.log(points.includes(search)) // => false :(
console.log(pipe(points, elem(EqPoint)(search))) // => true :)Quiz (JavaScript). Come mai usando includes ottengo false?
Aver catturato il concetto di uguaglianza è fondamentale, soprattutto in un linguaggio come JavaScript in cui alcune strutture dati possiedono delle API poco usabili rispetto ad un concetto di uguaglianza custom. E' anche il caso di Set per esempio:
type Point = {
readonly x: number
readonly y: number
}
const points: Set<Point> = new Set([{ x: 0, y: 0 }])
points.add({ x: 0, y: 0 })
console.log(points)
// => Set { { x: 0, y: 0 }, { x: 0, y: 0 } }Dato che Set utilizza === ("strict equality") come concetto di uguaglianza (fisso), points ora contiene due copie identiche di { x: 0, y: 0 }, un risultato certo non voluto. Conviene perciò definire una nuova API per aggiungere un elemento ad un Set che sfrutti l'astrazione Eq.
Quiz. Che firma potrebbe avere questa nuova API?
Per definire EqPoint occorre troppo boilerplate? La buona notizia è che la teoria ci dice che possiamo costruire una istanza di Eq per una struct come Point se siamo in grado di fornire una istanza di Eq per ogni suo campo.
Convenientemente il modulo fp-ts/Eq esporta un combinatore struct:
import { Eq, struct } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
type Point = {
readonly x: number
readonly y: number
}
const EqPoint: Eq<Point> = struct({
x: N.Eq,
y: N.Eq
})Nota. Esiste un combinatore simile a struct ma che lavora con le tuple: tuple
import { Eq, tuple } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
type Point = readonly [number, number]
const EqPoint: Eq<Point> = tuple(N.Eq, N.Eq)
console.log(EqPoint.equals([1, 2], [1, 2])) // => true
console.log(EqPoint.equals([1, 2], [1, -2])) // => falseCi sono altri combinatori messi a disposizione da fp-ts, ecco un combinatore che permette di derivare una istanza di Eq per i ReadonlyArray:
import { Eq, tuple } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
import * as RA from 'fp-ts/ReadonlyArray'
type Point = readonly [number, number]
const EqPoint: Eq<Point> = tuple(N.Eq, N.Eq)
const EqPoints: Eq<ReadonlyArray<Point>> = RA.getEq(EqPoint)Come succede con i semigruppi, potete definire più di una istanza di Eq per lo stesso tipo. Supponiamo di aver modellato un utente con il seguente tipo
type User = {
readonly id: number
readonly name: string
}possiamo definire una istanza di Eq "standard" usando il combinatore struct:
import { Eq, struct } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
import * as S from 'fp-ts/string'
type User = {
readonly id: number
readonly name: string
}
const EqStandard: Eq<User> = struct({
id: N.Eq,
name: S.Eq
})Nota. In un linguaggio come Haskell l'istanza di Eq standard per una struct come User può essere prodotta automaticamente dal compilatore.
data User = User Int String
deriving (Eq)Potremmo però avere delle situazioni particolari in cui ci può interessare avere un tipo di uguaglianza tra utenti differente, per esempio potremmo considerare due utenti uguali se hanno il campo id uguale
/** due utenti sono uguali se sono uguali il loro campi `id` */
const EqID: Eq<User> = {
equals: (first, second) => N.Eq.equals(first.id, second.id)
}Avendo "reificato" l'azione di confrontare due valori, cioè l'abbiamo resa concreta rappresentandola come una struttura dati, possiamo manipolare programmaticamente le istanze di Eq come facciamo per altre strutture dati, vediamo un esempio.
Esempio. Invece di definire EqId "a mano", possiamo utilizzare l'utile combinatore contramap: data una istanza di Eq per A e una funzione da B ad A, possiamo derivare una istanza di Eq per B
import { Eq, struct, contramap } from 'fp-ts/Eq'
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import * as S from 'fp-ts/string'
type User = {
readonly id: number
readonly name: string
}
const EqStandard: Eq<User> = struct({
id: N.Eq,
name: S.Eq
})
const EqID: Eq<User> = pipe(
N.Eq,
contramap((_: User) => _.id)
)
console.log(
EqStandard.equals({ id: 1, name: 'Giulio' }, { id: 1, name: 'Giulio Canti' })
) // => false (le proprietà `name` sono diverse)
console.log(
EqID.equals({ id: 1, name: 'Giulio' }, { id: 1, name: 'Giulio Canti' })
) // => true (nonostante le proprietà `name` siano diverse)
console.log(EqID.equals({ id: 1, name: 'Giulio' }, { id: 2, name: 'Giulio' }))
// => false (nonostante le proprietà `name` siano uguali)Quiz. Dato un tipo A, è possibile definire una istanza di semigruppo per Eq<A>? Cosa potrebbe rappresentare?
Ora che abbiamo modellato il concetto di uguaglianza, vediamo in questo capitolo come modellare il concetto di ordinamento.
Una relazione d'ordine totale può essere modellata in TypeScript con i seguenti tipi:
import { Eq } from 'fp-ts/Eq'
type Ordering = -1 | 0 | 1
interface Ord<A> extends Eq<A> {
readonly compare: (first: A, second: A) => Ordering
}Intuitivamente:
x < yse e solo secompare(x, y) = -1x = yse e solo secompare(x, y) = 0x > yse e solo secompare(x, y) = 1
Esempio
Proviamo a definire una istanza di Ord per il tipo number:
import { Ord } from 'fp-ts/Ord'
const OrdNumber: Ord<number> = {
equals: (first, second) => first === second,
compare: (first, second) => (first < second ? -1 : first > second ? 1 : 0)
}Devono valere le seguenti leggi:
- Reflexivity:
compare(x, x) <= 0, per ognixinA - Antisymmetry: se
compare(x, y) <= 0ecompare(y, x) <= 0allorax = y, per ognix,yinA - Transitivity: se
compare(x, y) <= 0ecompare(y, z) <= 0alloracompare(x, z) <= 0, per ognix,y,zinA
In più compare deve essere compatibile con l'operazione equals di Eq:
compare(x, y) === 0 se e solo se equals(x, y) === true, per ogni x, y in A
Nota. equals può essere derivato da compare nel modo seguente
equals: (first, second) => compare(first, second) === 0Perciò il modulo fp-ts/Ord esporta un comodo helper fromCompare che permette di definire una istanza di Ord semplicemente specificando la funzione compare:
import { Ord, fromCompare } from 'fp-ts/Ord'
const OrdNumber: Ord<number> = fromCompare((first, second) =>
first < second ? -1 : first > second ? 1 : 0
)Quiz. E' possibile definire un ordinamento per il gioco Sasso-Carta-Forbice compatibile con le mosse vincenti (ovvero move1 <= move2 se move2 batte move1)?
Come primo esempio di utilizzo definiamo una funzione sort che ordina gli elementi di un ReadonlyArray
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { Ord } from 'fp-ts/Ord'
export const sort = <A>(O: Ord<A>) => (
as: ReadonlyArray<A>
): ReadonlyArray<A> => as.slice().sort(O.compare)
pipe([3, 1, 2], sort(N.Ord), console.log) // => [1, 2, 3]Quiz (JavaScript). Perché nell'implementazione viene chiamato il metodo slice?
Come altro esempio di utilizzo definiamo una funzione min che restituisce il minimo fra due valori:
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { Ord } from 'fp-ts/Ord'
const min = <A>(O: Ord<A>) => (second: A) => (first: A): A =>
O.compare(first, second) === 1 ? second : first
pipe(2, min(N.Ord)(1), console.log) // => 1Così come possiamo invertire l'operazione concat per ottenere il semigruppo duale (con il combinatore reverse), così anche l'operazione compare può essere invertita per ottenere l'ordinamento duale.
Definiamo perciò il combinatore reverse per Ord:
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { fromCompare, Ord } from 'fp-ts/Ord'
export const reverse = <A>(O: Ord<A>): Ord<A> =>
fromCompare((first, second) => O.compare(second, first))Come esempio di utilizzo di reverse possiamo ricavare la funzione max dalla funzione min:
import { flow, pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { Ord, reverse } from 'fp-ts/Ord'
const min = <A>(O: Ord<A>) => (second: A) => (first: A): A =>
O.compare(first, second) === 1 ? second : first
// const max: <A>(O: Ord<A>) => (second: A) => (first: A) => A
const max = flow(reverse, min)
pipe(2, max(N.Ord)(1), console.log) // => 2La totalità dell'ordinamento (ovvero dati due qualsiasi x e y, una tra le seguenti condizioni vale: x <= y oppure y <= x) può sembrare ovvia quando parliamo di numeri, ma non è sempre così. Consideriamo un caso più complesso
type User = {
readonly name: string
readonly age: number
}Non è così chiaro stabilire quando un utente "è minore o uguale" ad un altro utente.
Come possiamo definire un Ord<User>?
Dipende davvero dal contesto, ma una possibile scelta potrebbe essere quella per esempio di ordinare gli utenti a seconda della loro età:
import * as N from 'fp-ts/number'
import { fromCompare, Ord } from 'fp-ts/Ord'
type User = {
readonly name: string
readonly age: number
}
const byAge: Ord<User> = fromCompare((first, second) =>
N.Ord.compare(first.age, second.age)
)Possiamo eliminare un po' di boilerplate usando il combinatore contramap: data una istanza di Ord per A e una funzione da B ad A, possiamo derivare una istanza di Ord per B:
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { contramap, Ord } from 'fp-ts/Ord'
type User = {
readonly name: string
readonly age: number
}
const byAge: Ord<User> = pipe(
N.Ord,
contramap((_: User) => _.age)
)Ora possiamo ottenere il più giovane di due utenti usando la funzione min che abbiamo precedentemente definito
// const getYounger: (second: User) => (first: User) => User
const getYounger = min(byAge)
pipe(
{ name: 'Guido', age: 50 },
getYounger({ name: 'Giulio', age: 47 }),
console.log
) // => { name: 'Giulio', age: 47 }Quiz. Nel modulo fp-ts/ReadonlyMap è contenuta la seguente API
/**
* Get a sorted `ReadonlyArray` of the keys contained in a `ReadonlyMap`.
*/
declare const keys: <K>(
O: Ord<K>
) => <A>(m: ReadonlyMap<K, A>) => ReadonlyArray<K>per quale motivo questa API richiede un Ord<K>?
Torniamo finalmente al quesito iniziale: definire i due semigruppi SemigroupMin e SemigroupMax anche per altri tipi oltre a number:
import { Semigroup } from 'fp-ts/Semigroup'
const SemigroupMin: Semigroup<number> = {
concat: (first, second) => Math.min(first, second)
}
const SemigroupMax: Semigroup<number> = {
concat: (first, second) => Math.max(first, second)
}Ora che abbiamo a disposizione l'astrazione Ord possiamo farlo:
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { Ord, contramap } from 'fp-ts/Ord'
import { Semigroup } from 'fp-ts/Semigroup'
export const min = <A>(O: Ord<A>): Semigroup<A> => ({
concat: (first, second) => (O.compare(first, second) === 1 ? second : first)
})
export const max = <A>(O: Ord<A>): Semigroup<A> => ({
concat: (first, second) => (O.compare(first, second) === 1 ? first : second)
})
type User = {
readonly name: string
readonly age: number
}
const byAge: Ord<User> = pipe(
N.Ord,
contramap((_: User) => _.age)
)
console.log(
min(byAge).concat({ name: 'Guido', age: 50 }, { name: 'Giulio', age: 47 })
) // => { name: 'Giulio', age: 47 }
console.log(
max(byAge).concat({ name: 'Guido', age: 50 }, { name: 'Giulio', age: 47 })
) // => { name: 'Guido', age: 50 }Esempio
Ricapitoliamo tutto con un esempio finale (adattato da Fantas, Eel, and Specification 4: Semigroup)
Supponiamo di dover costruire un sistema in cui, in un database, sono salvati dei record di un cliente, modellati nel seguente modo
interface Customer {
readonly name: string
readonly favouriteThings: ReadonlyArray<string>
readonly registeredAt: number // since epoch
readonly lastUpdatedAt: number // since epoch
readonly hasMadePurchase: boolean
}Per qualche ragione potreste finire per avere dei record duplicati per la stessa persona.
Abbiamo bisogno di una strategia di merging. Ma questo è proprio quello di cui si occupano i semigruppi!
import * as B from 'fp-ts/boolean'
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { contramap } from 'fp-ts/Ord'
import * as RA from 'fp-ts/ReadonlyArray'
import { max, min, Semigroup, struct } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'
interface Customer {
readonly name: string
readonly favouriteThings: ReadonlyArray<string>
readonly registeredAt: number // since epoch
readonly lastUpdatedAt: number // since epoch
readonly hasMadePurchase: boolean
}
const SemigroupCustomer: Semigroup<Customer> = struct({
// keep the longer name
name: max(pipe(N.Ord, contramap(S.size))),
// accumulate things
favouriteThings: RA.getSemigroup<string>(),
// keep the least recent date
registeredAt: min(N.Ord),
// keep the most recent date
lastUpdatedAt: max(N.Ord),
// boolean semigroup under disjunction
hasMadePurchase: B.SemigroupAny
})
console.log(
SemigroupCustomer.concat(
{
name: 'Giulio',
favouriteThings: ['math', 'climbing'],
registeredAt: new Date(2018, 1, 20).getTime(),
lastUpdatedAt: new Date(2018, 2, 18).getTime(),
hasMadePurchase: false
},
{
name: 'Giulio Canti',
favouriteThings: ['functional programming'],
registeredAt: new Date(2018, 1, 22).getTime(),
lastUpdatedAt: new Date(2018, 2, 9).getTime(),
hasMadePurchase: true
}
)
)
/*
{ name: 'Giulio Canti',
favouriteThings: [ 'math', 'climbing', 'functional programming' ],
registeredAt: 1519081200000, // new Date(2018, 1, 20).getTime()
lastUpdatedAt: 1521327600000, // new Date(2018, 2, 18).getTime()
hasMadePurchase: true
}
*/Quiz. Dato un tipo A è possibile definire una istanza di semigruppo per Ord<A>? Cosa potrebbe rappresentare?
Demo
Se aggiungiamo una condizione in più alla definizione di un semigruppo, ovvero che esista un elemento empty in A
tale che per ogni elemento a in A vale
- Right identity:
concat(a, empty) = a - Left identity:
concat(empty, a) = a
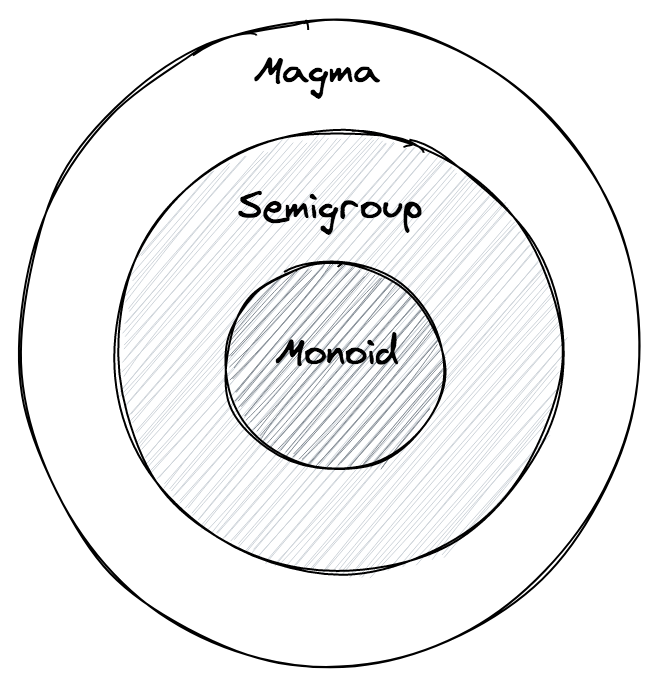
allora parliamo di monoide e l'elemento empty viene detto unità (o "elemento neutro").
Come già successo per Magma e Semigroup, i monoidi possono essere modellati con una interface di TypeScript:
import { Semigroup } from 'fp-ts/Semigroup'
interface Monoid<A> extends Semigroup<A> {
readonly empty: A
}Molti dei semigruppi che abbiamo visto nelle sezioni precedenti possono essere arricchiti e diventare istanze di Monoid:
import { Monoid } from 'fp-ts/Monoid'
/** number `Monoid` under addition */
const MonoidSum: Monoid<number> = {
concat: (first, second) => first + second,
empty: 0
}
/** number `Monoid` under multiplication */
const MonoidProduct: Monoid<number> = {
concat: (first, second) => first * second,
empty: 1
}
const MonoidString: Monoid<string> = {
concat: (first, second) => first + second,
empty: ''
}
/** boolean monoid under conjunction */
const MonoidAll: Monoid<boolean> = {
concat: (first, second) => first && second,
empty: true
}
/** boolean monoid under disjunction */
const MonoidAny: Monoid<boolean> = {
concat: (first, second) => first || second,
empty: false
}Quiz. Nella sezione sui semigruppi abbiamo visto che ReadonlyArray<string> ammette una istanza di Semigroup:
import { Semigroup } from 'fp-ts/Semigroup'
const Semigroup: Semigroup<ReadonlyArray<string>> = {
concat: (first, second) => first.concat(second)
}esiste anche l'unità? E' possibile generalizzare il risultato per ReadonlyArray<A> per qualsiasi tipo A?
Quiz (difficile). Dimostrare che, dato un monoide, l'elemento neutro è unico.
La conseguenza pratica è che se avete trovato una unità smettete di cercare!
Ogni monoide è un semigruppo, ma non ogni semigruppo è un monoide.
Esempio
Si consideri il seguente esempio:
import { pipe } from 'fp-ts/function'
import { intercalate } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'
const SemigroupIntercalate = pipe(S.Semigroup, intercalate('|'))
console.log(S.Semigroup.concat('a', 'b')) // => 'ab'
console.log(SemigroupIntercalate.concat('a', 'b')) // => 'a|b'
console.log(SemigroupIntercalate.concat('a', '')) // => 'a|'Notate come non sia possibile trovare un valore empty di tipo string tale che concat(a, empty) = a.
Infine un esempio più "esotico", sulle funzioni:
Esempio
Un endomorfismo è una funzione in cui il tipo in input e il tipo in output coincidono:
type Endomorphism<A> = (a: A) => ADato un tipo A, gli endomorfismi su A costituiscono un monoide, tale che:
- l'operazione
concatè l'usuale composizione di funzioni - l'unità è la funzione identità
import { Endomorphism, flow, identity } from 'fp-ts/function'
import { Monoid } from 'fp-ts/Monoid'
export const getEndomorphismMonoid = <A>(): Monoid<Endomorphism<A>> => ({
concat: flow,
empty: identity
})Quando usiamo un monoide invece di un semigruppo, la concatenazione di più elementi è ancora più semplice: non è necessario fornire esplicitamente un valore iniziale.
Quiz. Perché non è necessario fornire un valore iniziale?
import { concatAll } from 'fp-ts/Monoid'
import * as S from 'fp-ts/string'
import * as N from 'fp-ts/number'
import * as B from 'fp-ts/boolean'
console.log(concatAll(N.MonoidSum)([1, 2, 3, 4])) // => 10
console.log(concatAll(N.MonoidProduct)([1, 2, 3, 4])) // => 24
console.log(concatAll(S.Monoid)(['a', 'b', 'c'])) // => 'abc'
console.log(concatAll(B.MonoidAll)([true, false, true])) // => false
console.log(concatAll(B.MonoidAny)([true, false, true])) // => trueCome abbiamo già visto per i semigruppi, è possibile costruire una istanza di monoide per una struct se siamo in grado di fornire una istanza di monoide per ogni suo campo.
Esempio
import { Monoid, struct } from 'fp-ts/Monoid'
import * as N from 'fp-ts/number'
type Point = {
readonly x: number
readonly y: number
}
const Monoid: Monoid<Point> = struct({
x: N.MonoidSum,
y: N.MonoidSum
})Nota. Esiste un combinatore simile a struct ma che lavora con le tuple: tuple.
import { Monoid, tuple } from 'fp-ts/Monoid'
import * as N from 'fp-ts/number'
type Point = readonly [number, number]
const Monoid: Monoid<Point> = tuple(N.MonoidSum, N.MonoidSum)Quiz. E' possibile definire il "monoide libero" di un generico tipo A?
Demo (implementare un sistema per disegnare forme geometriche su un canvas)
Nel primo capitolo del corso abbiamo visto una definizione informale di funzione pura:
Una funzione pura è una procedura che dato lo stesso input restituisce sempre lo stesso output e non ha alcun side effect osservabile.
Un tale enunciato può lasciare spazio a qualche dubbio (per esempio, che cos'è un "side effect"?)
Vediamo perciò una definizione formale:
Ricordiamo che se X e Y sono due insiemi, allora con X × Y si indica il loro prodotto cartesiano, ovvero l'insieme
X × Y = { (x, y) | x ∈ X, y ∈ Y }
Definizione. Una funzione f: X ⟶ Y è un sottoinsieme f di X × Y tale che
per ogni x ∈ X esiste esattamente un y ∈ Y tale che la coppia (x, y) ∈ f.
L'insieme X si dice il dominio di f, Y il suo codominio.
Si noti che l'insieme f deve essere descritto staticamente in fase di definizione della funzione
(ovvero gli elementi di quell'insieme non possono variare nel tempo e per nessuna condizione interna o esterna).
Esempio
La funzione double: Nat ⟶ Nat, ove Nat è l'insieme dei numeri naturali, è il sottoinsieme del prodotto cartesiano Nat × Nat dato dalle coppie { (1, 2), (2, 4), (3, 6), ...}.
In TypeScript f potrebbe essere definita così:
const f: Record<number, number> = {
1: 2,
2: 4,
3: 6
...
}Quella dell'esempio viene detta definizione estensionale di una funzione, ovvero si enumerano uno per uno gli elementi del dominio e per ciascuno di essi si indica il corrispondente elemento del codominio. Naturalmente quando l'insieme è infinito, come in questo caso, la definizione può risultare un po' "scomoda".
Si può ovviare a questo problema introducendo quella che viene detta definizione intensionale,
ovvero si esprime una condizione che deve valere per tutte le coppie (x, y) appartenenti all'insieme f, ovvero y = x * 2. Questa è la forma familiare con cui scriviamo la funzione double e come la definiamo in TypeScript:
const double = (x: number): number => x * 2La definizione di funzione come sottoinsieme di un prodotto cartesiano mostra come in matematica tutte le funzioni siano pure: non c'è azione, modifica di stato o modifica degli elementi (che sono considerati immutabili) degli insiemi coinvolti. Nella programmazione funzionale l'implementazione delle funzioni deve tendere a questo modello ideale.
Quiz. Quali delle seguenti procedure sono funzioni pure?
const coefficient1 = 2
export const f1 = (n: number) => n * coefficient1
// ------------------------------------------------------
let coefficient2 = 2
export const f2 = (n: number) => n * coefficient2++
// ------------------------------------------------------
let coefficient3 = 2
export const f3 = (n: number) => n * coefficient3
// ------------------------------------------------------
export const f4 = (n: number) => {
const out = n * 2
console.log(out)
return out
}
// ------------------------------------------------------
interface User {
readonly id: number
readonly name: string
}
export declare const f5: (id: number) => Promise<User>
// ------------------------------------------------------
import * as fs from 'fs'
export const f6 = (path: string): string =>
fs.readFileSync(path, { encoding: 'utf8' })
// ------------------------------------------------------
export const f7 = (
path: string,
callback: (err: Error | null, data: string) => void
): void => fs.readFile(path, { encoding: 'utf8' }, callback)Che una funzione sia pura non implica necessariamente che sia bandita la mutabilità, localmente è ammissibile se non esce dai confini della implementazione.
Esempio (Implementazione della funzione concatAll dei monoidi)
import { Monoid } from 'fp-ts/Monoid'
const concatAll = <A>(M: Monoid<A>) => (as: ReadonlyArray<A>): A => {
let out: A = M.empty // <= mutabilità locale
for (const a of as) {
out = M.concat(out, a)
}
return out
}L'obbiettivo vero è sempre quello di garantire la proprietà fondamentale di trasparenza referenziale.
Il contratto che stipuliamo con l'utente della nostra API è definito dalla sua firma:
declare const concatAll: <A>(M: Monoid<A>) => (as: ReadonlyArray<A>) => Ae dalla promessa di rispettare la trasparenza referenziale, i dettagli tecnici di come la funzione è concretamente implementata non interessano e non sono sotto esame, c'è quindi la massima libertà.
Dunque come si definisce un "side effect"? Semplicemente negando la trasparenza referenziale:
Una espressione contiene un "side effect" se non gode della trasparenza referenziale.
Non solo le funzioni appoggiano sul primo dei due pilastri della programmazione funzionale, ma sono un esempio anche del secondo pilastro: la composizione.
Infatti le funzioni compongono:
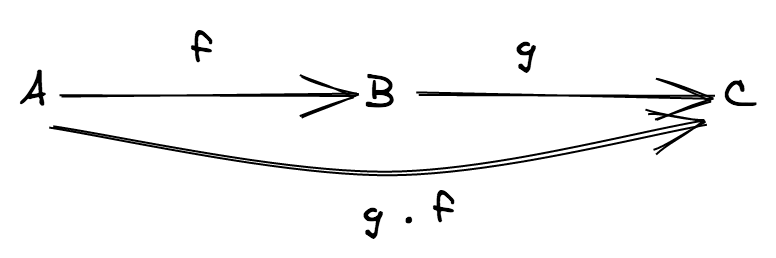
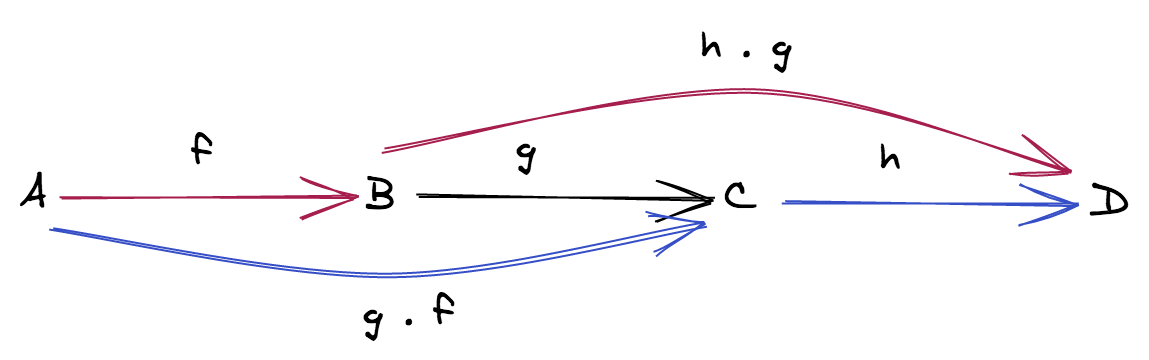
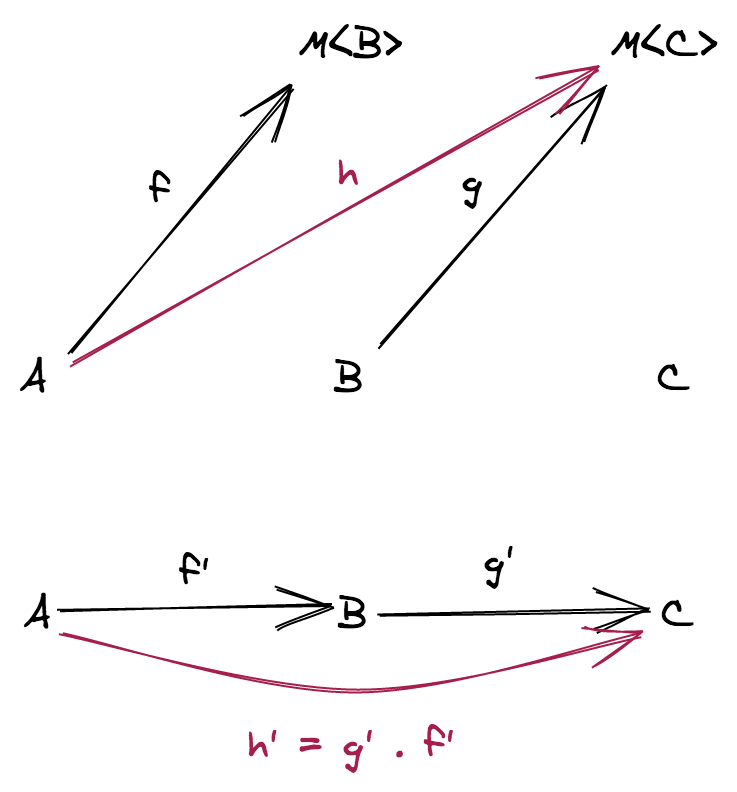
Definizione. Siano f: Y ⟶ Z e g: X ⟶ Y due funzioni, allora la funzione h: X ⟶ Z definita da
h(x) = f(g(x))
si dice composizione di f e g e si scrive h = f ∘ g
Si noti che affinché due funzioni f e g possano comporre, il dominio di f deve coincidere col codominio di g.
Definizione. Una funzione parziale è una funzione che non è definita per tutti i valori del dominio.
Viceversa una funzione definita per tutti i valori del dominio è detta totale.
Esempio
// Get the first element of a `ReadonlyArray`
declare const head: <A>(as: ReadonlyArray<A>) => AQuiz. Perché la funzione head è parziale?
Quiz. La funzione JSON.parse è totale?
parse: (text: string, reviver?: (this: any, key: string, value: any) => any) =>
anyQuiz. La funzione JSON.stringify è totale?
stringify: (
value: any,
replacer?: (this: any, key: string, value: any) => any,
space?: string | number
) => stringIn ambito funzionale si tende a definire solo funzioni pure e totali (d'ora in poi userò il termine "funzione" come sinonimo di "funzione pura e totale"), quindi come ci si deve comportare se si ha a che fare con una funzione parziale?
Fortunatamente una funzione parziale f: X ⟶ Y può essere sempre ricondotta ad una funzione totale aggiungendo al codominio un valore speciale non appartenente a Y, chiamiamolo None, e associandolo ad ogni valore di X per cui f non è definita
f': X ⟶ Y ∪ None
Chiamiamo Option(Y) = Y ∪ None.
f': X ⟶ Option(Y)
E' possibile definire Option(Y) in TypeScript? Nei prossimi due capitoli vedremo come poterlo fare.
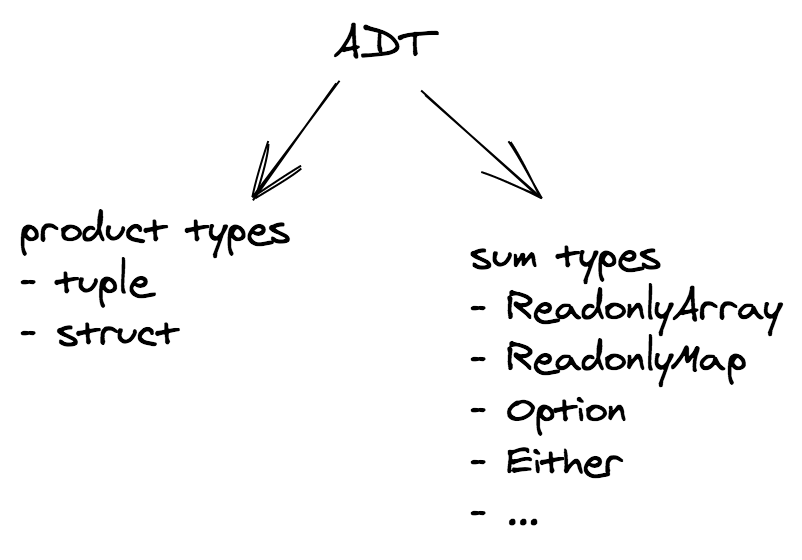
Un buon primo passo quando si sta construendo una nuova applicazione è quello di definire il suo modello di dominio. TypeScript offre molti strumenti che aiutano in questo compito. Gli Algebraic Data Types (abbreviato in ADT) sono uno di questi strumenti.
In computer programming, especially functional programming and type theory, an algebraic data type is a kind of composite type, i.e., a type formed by combining other types.
Due famiglie comuni di algebraic data types sono: product types e sum types.
Cominciamo da quelli più familiari: i product type.
Un product type è una collezione di tipi Ti indicizzati da un insieme I.
Due membri comuni di questa famiglia sono le n-tuple, dove I è un intervallo di numeri naturali:
type Tuple1 = [string] // I = [0]
type Tuple2 = [string, number] // I = [0, 1]
type Tuple3 = [string, number, boolean] // I = [0, 1, 2]
// Accessing by index
type Fst = Tuple2[0] // string
type Snd = Tuple2[1] // numbere le struct, ove I è un insieme di label:
// I = {"name", "age"}
interface Person {
name: string
age: number
}
// Accessing by label
type Name = Person['name'] // string
type Age = Person['age'] // numberI product type possono essere polimorfici.
Esempio
// ↓ type parameter
type HttpResponse<A> = {
readonly code: number
readonly body: A
}Se indichiamo con C(A) il numero di abitanti del tipo A, chiamata cardinalità, allora vale la seguente uguaglianza:
C([A, B]) = C(A) * C(B)la cardinalità del prodotto è il prodotto delle cardinalità
Esempio
Il tipo null ha cardinalità 1 perchè ha un solo abitante: null.
Esempio
Il tipo boolean ha cardinalità 2 perchè ha due abitanti: true e false.
Esempio
type Hour = 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12
type Period = 'AM' | 'PM'
type Clock = readonly [Hour, Period]Il tipo Hour ha 12 abitanti.
Il tipo Period ha 2 abitanti.
Il tipo Clock ha 12 * 2 = 24 abitanti.
Quiz. Quanti abitanti ha il seguente tipo Clock?
// same as before
type Hour = 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12
// same as before
type Period = 'AM' | 'PM'
type Clock = {
readonly hour: Hour
readonly period: Period
}Ogniqualvolta le sue componenti sono indipendenti.
type Clock = readonly [Hour, Period]Qui Hour e Period sono indipendenti, ovvero il valore di Hour non influisce sul valore di Period e viceversa, tutte le coppie sono legali e hanno senso.
Un sum type è una struttura dati che contiene un valore che può assumere diversi tipi (ma fissi). Solo uno dei tipi può essere in uso in un dato momento, e un campo che fa da "tag" indica quale di questi è in uso.
Nella documentazione ufficiale di TypeScript sono indicati col nome discriminated union.
E' importante sottolineare che i membri dell'unione che forma un sum type devono essere disgiunti, ovvero non devono esistere valori che appartengono a più di un membro.
Esempio
Il tipo
type StringsOrNumbers = ReadonlyArray<string> | ReadonlyArray<number>non è una unione disgiunta perché il valore [] (array vuoto) appartiene ad ambedue i membri dell'unione.
Quiz. La seguente unione è disgiunta?
type Member1 = { readonly a: string }
type Member2 = { readonly b: number }
type MyUnion = Member1 | Member2In programmazione funzionale si tende ad usare sempre unioni disgiunte.
Fortunatamente in TypeScript c'è un modo sicuro per garantire che una unione sia disgiunta: aggiungere un apposito campo che fa da tag.
Esempio (redux actions)
Il sum type Action modella una porzione delle operazioni che si possono compiere in una todo app.
export type Action =
| {
readonly type: 'ADD_TODO'
readonly text: string
}
| {
readonly type: 'UPDATE_TODO'
readonly id: number
readonly text: string
readonly completed: boolean
}
| {
readonly type: 'DELETE_TODO'
readonly id: number
}Il campo type, essendo obbligatorio e avendo un tipo diverso per ogni membro dell'unione, può essere eletto come tag e assicura che i membri siano disgiunti.
Nota. Il nome del campo che fa da tag è a discrezione dello sviluppatore, non deve essere necessariamente "type" (in fp-ts per esempio, per convenzione si usa il nome "_tag").
Ora che abbiamo visto un po' di esempi possiamo riformulare in modo più esplicito che cos'è un algebraic data type:
In general, an algebraic data type specifies a sum of one or more alternatives, where each alternative is a product of zero or more fields.
I sum type possono essere polimorfici e ricorsivi.
Esempio (linked lists)
// ↓ type parameter
export type List<A> =
| { readonly _tag: 'Nil' }
| { readonly _tag: 'Cons'; readonly head: A; readonly tail: List<A> }
// ↑ recursionQuiz (TypeScript). Delle seguenti strutture dati dire se sono dei product type o dei sum type
ReadonlyArray<A>Record<string, A>Record<'k1' | 'k2', A>ReadonlyMap<string, A>ReadonlyMap<'k1' | 'k2', A>
Un sum type con n membri necessita di (almeno) n costruttori, uno per ogni membro.
Esempio (redux action creators)
export type Action =
| {
readonly type: 'ADD_TODO'
readonly text: string
}
| {
readonly type: 'UPDATE_TODO'
readonly id: number
readonly text: string
readonly completed: boolean
}
| {
readonly type: 'DELETE_TODO'
readonly id: number
}
export const add = (text: string): Action => ({
type: 'ADD_TODO',
text
})
export const update = (
id: number,
text: string,
completed: boolean
): Action => ({
type: 'UPDATE_TODO',
id,
text,
completed
})
export const del = (id: number): Action => ({
type: 'DELETE_TODO',
id
})Esempio (TypeScript, linked lists)
export type List<A> =
| { readonly _tag: 'Nil' }
| { readonly _tag: 'Cons'; readonly head: A; readonly tail: List<A> }
// a nullary constructor can be implemented as a constant
export const nil: List<never> = { _tag: 'Nil' }
export const cons = <A>(head: A, tail: List<A>): List<A> => ({
_tag: 'Cons',
head,
tail
})
// equivalente ad un array [1, 2, 3]
const myList = cons(1, cons(2, cons(3, nil)))Esempio (Haskell, linked lists)
data List a = Nil | Cons a (List a)
myList :: List Int
myList = Cons 1 (Cons 2 (Cons 3 Nil))JavaScript non ha il pattern matching (e quindi neanche TypeScript).
Esempio (Haskell, linked lists)
data List a = Nil | Cons a (List a)
-- restituisce `True` se la lista è vuota
isEmpty :: List a -> Bool
isEmpty Nil = True
isEmpty (Cons _ _) = FalseTuttavia possiamo simulare il pattern matching tramite una funzione match.
Esempio (TypeScript, linked lists)
interface Nil {
readonly _tag: 'Nil'
}
interface Cons<A> {
readonly _tag: 'Cons'
readonly head: A
readonly tail: List<A>
}
export type List<A> = Nil | Cons<A>
export const match = <R, A>(
onNil: () => R,
onCons: (head: A, tail: List<A>) => R
) => (fa: List<A>): R => {
switch (fa._tag) {
case 'Nil':
return onNil()
case 'Cons':
return onCons(fa.head, fa.tail)
}
}
// restituisce `true` se la lista è vuota
export const isEmpty = match(
() => true,
() => false
)
// restituisce il primo elemento della lista oppure `undefined`
export const head = match(
() => undefined,
(head, _tail) => head
)
// calcola la lunghezza di una lista (ricorsivamente)
export const length: <A>(fa: List<A>) => number = match(
() => 0,
(_, tail) => 1 + length(tail)
)Quiz. Perchè l'API head è sub ottimale?
Nota. TypeScript offre una ottima feature legata ai sum type: exhaustive check. Ovvero il type checker è in grado di determinare se tutti i casi sono stati gestiti nello switch definito nel body della funzione match.
Vale la seguente uguaglianza:
C(A | B) = C(A) + C(B)la cardinalità della somma è la somma delle cardinalità
Esempio (the Option type)
interface None {
readonly _tag: 'None'
}
interface Some<A> {
readonly _tag: 'Some'
readonly value: A
}
type Option<A> = None | Some<A>Dalla formula generale ottengo C(Option<A>) = C(None) + C(Some<A>) = 1 + C(A), da cui possiamo derivare per esempio la cardinalità di Option<boolean>, ovvero 1 + 2 = 3 abitanti:
{ _tag: 'None' }{ _tag: 'Some', value: true }{ _tag: 'Some', value: false }
Quando le sue componenti sarebbero dipendenti se implementate con un product type.
Esempio (React props)
import * as React from 'react'
interface Props {
readonly editable: boolean
readonly onChange?: (text: string) => void
}
class Textbox extends React.Component<Props> {
render() {
if (this.props.editable) {
// error: Cannot invoke an object which is possibly 'undefined' :(
this.props.onChange('a')
}
return <div />
}
}Il problema qui è che Props è modellato come un prodotto ma onChange dipende da editable.
Un sum type è una scelta migliore:
import * as React from 'react'
type Props =
| {
readonly type: 'READONLY'
}
| {
readonly type: 'EDITABLE'
readonly onChange: (text: string) => void
}
class Textbox extends React.Component<Props> {
render() {
switch (this.props.type) {
case 'EDITABLE':
this.props.onChange('a') // :)
}
return <div />
}
}Esempio (node callbacks)
declare function readFile(
path: string,
// ↓ ---------- ↓ CallbackArgs
callback: (err?: Error, data?: string) => void
): voidIl risultato dell'operazione readFile è modellato con un product type (più precisamente una tupla) che viene passato come input alla funzione callback:
type CallbackArgs = [Error | undefined, string | undefined]tuttavia le sue componenti sono dipendenti: si riceve un errore oppure una stringa:
| err | data | legale? |
|---|---|---|
Error |
undefined |
✓ |
undefined |
string |
✓ |
Error |
string |
✘ |
undefined |
undefined |
✘ |
Questa API non è modellata seguendo questo adagio:
Make impossible state unrepresentable
Un sum type sarebbe una scelta migliore, ma quale? Vediamo come si gestiscono gli errori in modo funzionale.
Quiz. Recentemente alle API a callback si preferiscono le API che restituiscono una Promise
declare function readFile(path: string): Promise<string>potete indicare un contro di questa seconda soluzione quando si utilizza un linguaggio a tipi statici come TypeScript?
Vediamo come gestire gli errori in modo funzionale.
Una funzione che restituisce un errore o lancia una eccezione è un esempio di funzione parziale.
Nel capitolo Funzioni pure e funzioni parziali abbiamo visto che ogni funzione parziale f può essere sempre ricondotta ad una funzione totale f'
f': X ⟶ Option(Y)
Ora che sappiamo qualcosa di più sui sum type in TypeScript possiamo definire Option senza ulteriore indugio.
Il tipo Option<A> rappresenta l'effetto di una computazione che può fallire (caso None) oppure restituire un valore di tipo A (caso Some):
// represents a failure
interface None {
readonly _tag: 'None'
}
// represents a success
interface Some<A> {
readonly _tag: 'Some'
readonly value: A
}
type Option<A> = None | Some<A>Vediamone anche i costruttori e la sua funzione match di "pattern matching":
const none: Option<never> = { _tag: 'None' }
const some = <A>(value: A): Option<A> => ({ _tag: 'Some', value })
const match = <R, A>(onNone: () => R, onSome: (a: A) => R) => (
fa: Option<A>
): R => {
switch (fa._tag) {
case 'None':
return onNone()
case 'Some':
return onSome(fa.value)
}
}Il tipo Option può essere usato per evitare di lanciare eccezioni e/o rappresentare i valori opzionali, così possiamo passare da:
// this is a lie ↓
const head = <A>(as: ReadonlyArray<A>): A => {
if (as.length === 0) {
throw new Error('Empty array')
}
return as[0]
}
let s: string
try {
s = String(head([]))
} catch (e) {
s = e.message
}in cui il type system è all'oscuro di un possibile fallimento, a:
import { pipe } from 'fp-ts/function'
// ↓ the type system "knows" that this computation may fail
const head = <A>(as: ReadonlyArray<A>): Option<A> =>
as.length === 0 ? none : some(as[0])
declare const numbers: ReadonlyArray<number>
const result = pipe(
head(numbers),
match(
() => 'Empty array',
(n) => String(n)
)
)ove la possibilità di errore è codificata nel type system.
Infatti se proviamo ad accedere alla proprietà value di una Option senza controllare in quale dei due casi siamo, il type system ci avverte del possibile errore:
declare const numbers: ReadonlyArray<number>
const result = head(numbers)
result.value // type checker error: Property 'value' does not exist on type 'Option<number>'L'unico modo per accedere al valore contenuto in una Option è gestire anche il caso di fallimento utilizzando la funzione match
pipe(result, match(
() => ...handle error...
(n) => ...go on with my business logic...
))E' possibile definire delle istanze per le astrazioni che abbiamo visto nei capitoli precedenti? Cominciamo da Eq.
Supponiamo di avere due valori di tipo Option<string> e volerli confrontare per capire se sono uguali:
import { pipe } from 'fp-ts/function'
import { match, Option } from 'fp-ts/Option'
declare const o1: Option<string>
declare const o2: Option<string>
const result: boolean = pipe(
o1,
match(
// onNone o1
() =>
pipe(
o2,
match(
// onNone o2
() => true,
// onSome o2
() => false
)
),
// onSome o1
(s1) =>
pipe(
o2,
match(
// onNone o2
() => false,
// onSome o2
(s2) => s1 === s2 // <= qui uso l'uguaglianza tra stringhe
)
)
)
)E se avessimo due Option<number>? Il codice sarebbe pressoché uguale tranne alla fine quando confronto i valori contenuti nelle due Option, per i quali userò l'uguaglianza tra numeri.
Ma allora possiamo generalizzare il codice richiedendo all'utente una istanza di Eq per A e quindi derivare una istanza di Eq per Option<A>.
In altre parole possiamo definire un combinatore getEq: dato un Eq<A> il combinatore restituisce un Eq<Option<A>>:
import { Eq } from 'fp-ts/Eq'
import { pipe } from 'fp-ts/function'
import { match, Option, none, some } from 'fp-ts/Option'
export const getEq = <A>(E: Eq<A>): Eq<Option<A>> => ({
equals: (first, second) =>
pipe(
first,
match(
() =>
pipe(
second,
match(
() => true,
() => false
)
),
(a1) =>
pipe(
second,
match(
() => false,
(a2) => E.equals(a1, a2) // <= qui uso l'uguaglianza tra `A`
)
)
)
)
})
import * as S from 'fp-ts/string'
const EqOptionString = getEq(S.Eq)
console.log(EqOptionString.equals(none, none)) // => true
console.log(EqOptionString.equals(none, some('b'))) // => false
console.log(EqOptionString.equals(some('a'), none)) // => false
console.log(EqOptionString.equals(some('a'), some('b'))) // => false
console.log(EqOptionString.equals(some('a'), some('a'))) // => trueNaturalmente possiamo usare tutti i combinatori già visti per Eq, ad esempio ecco come definire una istanza di Eq per Option<readonly [string, number]>:
import { tuple } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
import { getEq, Option, some } from 'fp-ts/Option'
import * as S from 'fp-ts/string'
type MyTuple = readonly [string, number]
const EqMyTuple = tuple<MyTuple>(S.Eq, N.Eq)
const EqOptionMyTuple = getEq(EqMyTuple)
const o1: Option<MyTuple> = some(['a', 1])
const o2: Option<MyTuple> = some(['a', 2])
const o3: Option<MyTuple> = some(['b', 1])
console.log(EqOptionMyTuple.equals(o1, o1)) // => true
console.log(EqOptionMyTuple.equals(o1, o2)) // => false
console.log(EqOptionMyTuple.equals(o1, o3)) // => falseSe modifichiamo di poco gli import dello snippet precedente possiamo ottenere un risultato analogo per Ord:
import * as N from 'fp-ts/number'
import { getOrd, Option, some } from 'fp-ts/Option'
import { tuple } from 'fp-ts/Ord'
import * as S from 'fp-ts/string'
type MyTuple = readonly [string, number]
const OrdMyTuple = tuple<MyTuple>(S.Ord, N.Ord)
const OrdOptionMyTuple = getOrd(OrdMyTuple)
const o1: Option<MyTuple> = some(['a', 1])
const o2: Option<MyTuple> = some(['a', 2])
const o3: Option<MyTuple> = some(['b', 1])
console.log(OrdOptionMyTuple.compare(o1, o1)) // => 0
console.log(OrdOptionMyTuple.compare(o1, o2)) // => -1
console.log(OrdOptionMyTuple.compare(o1, o3)) // => -1Ora supponiamo di voler fare un "merge" di due Option<A>, ci sono quattro casi:
| x | y | concat(x, y) |
|---|---|---|
| none | none | none |
| some(a1) | none | none |
| none | some(a2) | none |
| some(a1) | some(a2) | ? |
C'è un problema nell'ultimo caso, ci occorre un modo per fare un "merge" di due A.
Ma questo è proprio il lavoro di Semigroup!
| x | y | concat(x, y) |
|---|---|---|
| some(a1) | some(a2) | some(S.concat(a1, a2)) |
Possiamo richiedere una istanza di semigruppo per A e quindi derivare una istanza di semigruppo per Option<A>
// l'implementazione è lasciata come esercizio
declare const getApplySemigroup: <A>(S: Semigroup<A>) => Semigroup<Option<A>>Quiz. E' possibile aggiungere un elemento neutro al semigruppo precedente rendendolo un monoide?
// l'implementazione è lasciata come esercizio
declare const getApplicativeMonoid: <A>(M: Monoid<A>) => Monoid<Option<A>>E' possibile definire una istanza di monoide per Option<A> che si comporta nel modo seguente:
| x | y | concat(x, y) |
|---|---|---|
| none | none | none |
| some(a1) | none | some(a1) |
| none | some(a2) | some(a2) |
| some(a1) | some(a2) | some(S.concat(a1, a2)) |
// l'implementazione è lasciata come esercizio
declare const getMonoid: <A>(S: Semigroup<A>) => Monoid<Option<A>>Quiz. Qual'è l'elemento neutro empty del monoide?
Esempio
Usando getMonoid possiamo derivare altri due utili monoidi:
(Monoid returning the left-most non-None value)
| x | y | concat(x, y) |
|---|---|---|
| none | none | none |
| some(a1) | none | some(a1) |
| none | some(a2) | some(a2) |
| some(a1) | some(a2) | some(a1) |
import { Monoid } from 'fp-ts/Monoid'
import { getMonoid, Option } from 'fp-ts/Option'
import { first } from 'fp-ts/Semigroup'
export const getFirstMonoid = <A = never>(): Monoid<Option<A>> =>
getMonoid(first())e il suo duale:
(Monoid returning the right-most non-None value)
| x | y | concat(x, y) |
|---|---|---|
| none | none | none |
| some(a1) | none | some(a1) |
| none | some(a2) | some(a2) |
| some(a1) | some(a2) | some(a2) |
import { Monoid } from 'fp-ts/Monoid'
import { getMonoid, Option } from 'fp-ts/Option'
import { last } from 'fp-ts/Semigroup'
export const getLastMonoid = <A = never>(): Monoid<Option<A>> =>
getMonoid(last())Esempio
In particolare getLastMonoid può essere utile per gestire valori opzionali:
import { Monoid, struct } from 'fp-ts/Monoid'
import { getMonoid, none, Option, some } from 'fp-ts/Option'
import { last } from 'fp-ts/Semigroup'
/** VSCode settings */
interface Settings {
/** Controls the font family */
readonly fontFamily: Option<string>
/** Controls the font size in pixels */
readonly fontSize: Option<number>
/** Limit the width of the minimap to render at most a certain number of columns. */
readonly maxColumn: Option<number>
}
const monoidSettings: Monoid<Settings> = struct({
fontFamily: getMonoid(last()),
fontSize: getMonoid(last()),
maxColumn: getMonoid(last())
})
const workspaceSettings: Settings = {
fontFamily: some('Courier'),
fontSize: none,
maxColumn: some(80)
}
const userSettings: Settings = {
fontFamily: some('Fira Code'),
fontSize: some(12),
maxColumn: none
}
/** userSettings overrides workspaceSettings */
console.log(monoidSettings.concat(workspaceSettings, userSettings))
/*
{ fontFamily: some("Fira Code"),
fontSize: some(12),
maxColumn: some(80) }
*/Quiz. Supponiamo che VSCode non possa gestire delle colonne più larghe di 80, come potremmo modificare la definizione di monoidSettings per tenerne conto?
Un uso comune di Either è come alternativa ad Option per gestire l'effetto di una computazione che può fallire, potendo però specificare il motivo del fallimento.
In questo uso, None è sostituito da Left che contiene informazione utile relativa all'errore. Right invece sostituisce Some.
// represents a failure
interface Left<E> {
readonly _tag: 'Left'
readonly left: E
}
// represents a success
interface Right<A> {
readonly _tag: 'Right'
readonly right: A
}
type Either<E, A> = Left<E> | Right<A>Costruttori e pattern matching:
const left = <E, A>(left: E): Either<E, A> => ({ _tag: 'Left', left })
const right = <A, E>(right: A): Either<E, A> => ({ _tag: 'Right', right })
const match = <E, R, A>(onLeft: (left: E) => R, onRight: (right: A) => R) => (
fa: Either<E, A>
): R => {
switch (fa._tag) {
case 'Left':
return onLeft(fa.left)
case 'Right':
return onRight(fa.right)
}
}Tornando all'esempio con la callback:
declare function readFile(
path: string,
callback: (err?: Error, data?: string) => void
): void
readFile('./myfile', (err, data) => {
let message: string
if (err !== undefined) {
message = `Error: ${err.message}`
} else if (data !== undefined) {
message = `Data: ${data.trim()}`
} else {
// should never happen
message = 'The impossible happened'
}
console.log(message)
})possiamo cambiare la sua firma in:
declare function readFile(
path: string,
callback: (result: Either<Error, string>) => void
): voide consumare l'API in questo modo:
readFile('./myfile', (e) =>
pipe(
e,
match(
(err) => `Error: ${err.message}`,
(data) => `Data: ${data.trim()}`
),
console.log
)
)Abbiamo visto che una pietra miliare della programmazione funzionale è la composizione.
And how do we solve problems? We decompose bigger problems into smaller problems. If the smaller problems are still too big, we decompose them further, and so on. Finally, we write code that solves all the small problems. And then comes the essence of programming: we compose those pieces of code to create solutions to larger problems. Decomposition wouldn't make sense if we weren't able to put the pieces back together. - Bartosz Milewski
Ma cosa significa esattamente? Quando possiamo dire che due cose compongono? E quando possiamo dire che due cose compongono bene?
Entities are composable if we can easily and generally combine their behaviors in some way without having to modify the entities being combined. I think of composability as being the key ingredient necessary for acheiving reuse, and for achieving a combinatorial expansion of what is succinctly expressible in a programming model. - Paul Chiusano
Nel primo capitolo abbiamo appreso che un programma in stile funzionale tende ad essere scritto come una pipeline:
const program = pipe(
input,
f1, // funzione pura
f2, // funzione pura
f3, // funzione pura
...
)Ma quanto è facile attenersi a questo stile? E' davvero fattibile questa cosa? Proviamoci:
import { pipe } from 'fp-ts/function'
import * as RA from 'fp-ts/ReadonlyArray'
const double = (n: number): number => n * 2
/**
* Dato un ReadonlyArray<number> il programma restituisce il primo elemento raddoppiato
*/
const program = (input: ReadonlyArray<number>): number =>
pipe(
input,
RA.head, // errore di compilazione! Type 'Option<number>' is not assignable to type 'number'
double
)Perché ottengo un errore di compilazione?
Il fatto è che head e double non compongono!
head: (as: ReadonlyArray<number>) => Option<number>
double: (n: number) => numberil codominio di head non coincide con il dominio di double.
Che fare allora? Rinunciare?
Occorrerebbe poter fare riferimento ad una teoria rigorosa che possa fornire risposte a domande così fondamentali. Ci occorre una definizione formale del concetto di composizione.
Fortunatamente da più di 70 anni un vasto gruppo di studiosi appartenenti al più longevo e mastodontico progetto open source nella storia dell'umanità (la matematica) si occupa di sviluppare una teoria specificatamente dedicata a questo argomento: la teoria delle categorie, fondata da Saunders Mac Lane, insieme a Samuel Eilenberg (1945).
(Saunders Mac Lane)
(Samuel Eilenberg)
Vedremo nei prossimi capitoli come una categoria possa costituire:
- un modello di un generico linguaggio di programmazione
- un modello per il concetto di composizione
Categories capture the essence of composition.
La definizione di categoria, anche se non particolarmente complicata, è un po' lunga perciò la dividerò in due parti:
- la prima è tecnica (prima di tutto dobbiamo definire i suoi costituenti)
- la seconda parte contiene ciò a cui siamo più interessati: una nozione di composizione
Parte I (Costituenti)
Una categoria è una coppia (Objects, Morphisms) ove:
Objectsè una collezione di oggettiMorphismsè una collezione di morfismi (dette anche "frecce") tra oggetti
Nota. Il termine "oggetto" non ha niente a che fare con la OOP, pensate agli oggetti come a scatole nere che non potete ispezionare, oppure come a dei semplici placeholder utili a definire i morfismi.
Ogni morfismo f possiede un oggetto sorgente A e un oggetto target B, dove sia A che B sono contenuti in Objects. Scriviamo f: A ⟼ B e diciamo che "f è un morfismo da A a B"
Nota. Per semplicità d'ora in poi nei grafici userò solo le etichette per gli oggetti, omettendo il cerchietto.
Parte II (Composizione)
Esiste una operazione ∘, chiamata "composizione", tale che valgono le seguenti proprietà:
(composition of morphisms) ogni volta che f: A ⟼ B and g: B ⟼ C sono due morfismi in Morphisms allora deve esistere un terzo morfismo g ∘ f: A ⟼ C in Morphisms che è detto la composizione di f e g
(associativity) se f: A ⟼ B, g: B ⟼ C e h: C ⟼ D allora h ∘ (g ∘ f) = (h ∘ g) ∘ f
(identity) per ogni oggetto X, esiste un morfismo idX: X ⟼ X chiamato il morfismo identità di X, tale che per ogni morfismo f: A ⟼ X e ogni morfismo g: X ⟼ B, vale idX ∘ f = f e g ∘ idX = g.
Vediamo un piccolo esempio
Esempio
Questa categoria è molto semplice, ci sono solo tre oggetti e sei morfismi (idA, idB, idC sono i morfismi identità di A, B, C).
Una categoria può essere interpretata come un modello semplificato di un typed programming language, ove:
- gli oggetto sono tipi
- i morfismi sono funzioni
∘è l'usuale composizione di funzioni
Il diagramma:
può perciò essere interpretato come un immaginario (e molto semplice) linguaggio di programmazione con solo tre tipi e sei funzioni.
Per esempio potremmo pensare a:
A = stringB = numberC = booleanf = string => numberg = number => booleang ∘ f = string => boolean
L'implementazione potrebbe essere qualcosa come:
const idA = (s: string): string => s
const idB = (n: number): number => n
const idC = (b: boolean): boolean => b
const f = (s: string): number => s.length
const g = (n: number): boolean => n > 2
// gf = g ∘ f
const gf = (s: string): boolean => g(f(s))Possiamo definire una categoria, chiamiamola TS, come modello semplificato del linguaggio TypeScript, ove:
- gli oggetti sono tutti i tipi di TypeScript:
string,number,ReadonlyArray<string>, ecc... - i morfismi sono tutte le funzioni di TypeScript:
(a: A) => B,(b: B) => C, ecc... oveA,B,C, ... sono tipi di TypeScript - i morfismi identità sono tutti codificati da una singola funzione polimorfica
const identity = <A>(a: A): A => a - la composizione di morfismi è l'usuale composizione di funzione (che è associativa)
Come modello di TypeScript, la categoria TS a prima vista può sembrare troppo limitata: non ci sono cicli, niente if, non c'è quasi nulla... e tuttavia questo modello semplificato è abbastanza ricco per soddisfare il nostro obbiettivo principale: ragionare su una nozione ben definita di composizione.
Ora che abbiamo un semplice modello per il nostro linguaggio di programmazione, affrontiamo il problema centrale della composizione.
In TS possiamo comporre due funzioni generiche f: (a: A) => B and g: (c: C) => D fintanto che C = B.
Se sussiste questa condizione possiamo utilizzare le funzioni flow (o pipe):
function flow<A, B, C>(f: (a: A) => B, g: (b: B) => C): (a: A) => C {
return (a) => g(f(a))
}
function pipe<A, B, C>(a: A, f: (a: A) => B, g: (b: B) => C): C {
return flow(f, g)(a)
}Ma che succede se B != C? Come possiamo comporre due funzioni con queste caratteristiche?
Nei prossimi capitoli vedremo sotto quali condizioni una tale composizione è possibile.
Spoiler
- per comporre
f: (a: A) => Bcong: (b: B) => Cabbiamo solo bisogno della usuale composizione di funzioni - per comporre
f: (a: A) => F<B>cong: (b: B) => Cabbiamo bisogno di una istanza di funtore perF - per comporre
f: (a: A) => F<B>cong: (b: B, c: C) => Dabbiamo bisogno di una istanza di funtore applicativo perF - per comporre
f: (a: A) => F<B>cong: (b: B) => F<C>abbiamo bisogno di una istanza di monade perF
Il problema da cui siamo partiti all'inizio del capitolo corrisponde alla situazione ②, quando al posto del generico F mettiamo Option:
// A = ReadonlyArray<number>, B = number, F = Option
head: (as: ReadonlyArray<number>) => Option<number>
double: (n: number) => numberPer risolverlo il prossimo capitolo parlerà di funtori.
Nell'ultimo capitolo ho presentato la categoria TS (la categoria di TypeScript) e il problema centrale con la composizione di funzioni:
Come possiamo comporre due funzioni generiche
f: (a: A) => Beg: (c: C) => D?
Ma perché trovare soluzioni a questo problema è così importante?
Perché, se è vero che le categorie possono essere usate per modellare i linguaggi di programmazione, i morfismi (ovvero le funzioni in TS) possono essere usate per modellare i programmi.
Perciò risolvere quel problema astratto significa anche trovare un modo di comporre i programmi in modo generico. E questo sì che è molto interessante per uno sviluppatore, non è vero?
Se vogliamo usare le funzioni per modellare i programmi dobbiamo affrontare subito un problema:
Come è possibile modellare un programma che produce side effect con una funzione pura?
La risposta è modellare i side effect tramite quelli che vengono chiamati effetti, ovvero tipi che rappresentano i side effect.
Vediamo due tecniche possibili per farlo in JavaScript:
- definire un DSL (domain specific language) per gli effetti
- usare i thunk
La prima tecnica, usare cioè un DSL, significa modificare un programma come:
const log = (message: string): void => {
console.log(message) // side effect
}cambiando il suo codominio e facendo in modo che sia una funzione che restituisce una descrizione del side effect:
type DSL = ... // sum type di tutti i possibili effetti gestiti dal sistema
const log = (message: string): DSL => {
return { _tag: 'log', message } // un effetto che descrive l'atto di scrivere sulla console
}Quiz (JavaScript). La funzione log appena definita è davvero pura? Eppure log('foo') !== log('foo')!
Questa prima tecnica presuppone un modo per combinare gli effetti e la definizione di un interprete in grado di eseguire concretamente gli effetti quando si vuole lanciare il programma finale.
Una seconda tecnica, più semplice e possibile in TypeScript, è racchiudere la computazione in un thunk:
// un thunk che rappresenta un side effect sincrono
type IO<A> = () => A
const log = (message: string): IO<void> => {
return () => console.log(message) // restituisce un thunk
}Il programma log, quando viene eseguito, non provoca immediatamente il side effect ma restituisce un valore che rappresenta la computazione.
import { IO } from 'fp-ts/IO'
export const log = (message: string): IO<void> => {
return () => console.log(message) // restituisce un thunk
}
export const main = log('hello!')
// a questo punto non vedo nulla sulla console
// perchè `main` è solo un valore inerte
// che rappresenta la computazione
main()
// solo dopo aver lanciato esplicitamente il programma
// vedo il risultato sulla consoleNella programmazione funzionale si tende a spingere i side effect (sottoforma di effetti) ai confini del sistema (ovvero la funzione main)
ove vengono eseguiti, si ottiene perciò il seguente schema:
system = pure core + imperative shell
Nei linguaggi puramente funzionali (come Haskell, PureScript o Elm) questa divisione è netta ed è imposta dal linguaggio stesso.
Anche con questa seconda tecnica (quella usata da fp-ts) occorre un modo per combinare gli effetti, il che ci riporta alla nostra volontà di comporre i programmi in modo generico, vediamo come fare.
Innanzi tutto un po' di terminologia (informale): chiamiamo programma puro una funzione con la seguente firma:
(a: A) => B
Una tale firma modella un programma che accetta un input di tipo A e restituisce un risultato di tipo B, senza alcun effetto.
Esempio
Il programma len:
const len = (s: string): number => s.lengthChiamiamo programma con effetti una funzione con la seguente firma:
(a: A) => F<B>
per un qualche type constructor F.
Ricordiamo che un type constructor è un operatore a livello di tipi n-ario che prende come argomento zero o più tipi e che restituisce un tipo (esempi: Option, ReadonlyArray).
Una tale firma modella un programma che accetta un input di tipo A e restituisce un risultato di tipo B insieme ad un effetto F.
Esempio
Il programma head
import { Option, some, none } from 'fp-ts/Option'
const head = <A>(as: ReadonlyArray<A>): Option<A> =>
as.length === 0 ? none : some(as[0])è un programma con effetto Option.
Quando parliamo di effetti siamo interessati a type constructor n-ari con n >= 1, per esempio:
| Type constructor | Effect (interpretation) |
|---|---|
ReadonlyArray<A> |
a non deterministic computation |
Option<A> |
a computation that may fail |
Either<E, A> |
a computation that may fail |
IO<A> |
a synchronous computation that never fails |
Task<A> |
an asynchronous computation never fails |
Reader<R, A> |
reading from an environment |
ove
// un thunk che restituisce una `Promise`
type Task<A> = () => Promise<A>// `R` represents an "environment" needed for the computation
// (we can "read" from it) and `A` is the result
type Reader<R, A> = (r: R) => ATorniamo ora al nostro problema principale:
Come possiamo comporre due funzioni generiche
f: (a: A) => Beg: (c: C) => D?
Dato che il problema generale non è trattabile, dobbiamo aggiungere qualche vincolo a B e C.
Sappiamo già che se B = C allora la soluzione è l'usuale composizione di funzioni
function flow<A, B, C>(f: (a: A) => B, g: (b: B) => C): (a: A) => C {
return (a) => g(f(a))
}Ma cosa fare negli altri casi?
Consideriamo il seguente vincolo: B = F<C> per un qualche type constructor F, abbiamo perciò la seguente situazione:
f: (a: A) => F<B>è un programma con effettig: (b: B) => Cè un programma puro
Per poter comporre f con g dobbiamo trovare un procedimento che permetta di tramutare g da una funzione (b: B) => C ad una funzione (fb: F<B>) => F<C> in modo tale che possiamo usare la normale composizione di funzioni (infatti in questo modo il codominio di f sarebbe lo stesso insieme che fa da dominio della nuova funzione).
Abbiamo perciò tramutato il problema originale in uno nuovo e diverso: possiamo trovare una funzione, chiamiamola map, che agisce in questo modo?
Vediamo qualche esempio pratico:
Esempio (F = ReadonlyArray)
import { flow, pipe } from 'fp-ts/function'
// trasforma funzioni `B -> C` in funzioni `ReadonlyArray<B> -> ReadonlyArray<C>`
const map = <B, C>(g: (b: B) => C) => (
fb: ReadonlyArray<B>
): ReadonlyArray<C> => fb.map(g)
// -------------------
// esempio di utilizzo
// -------------------
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const getFollowers = (user: User): ReadonlyArray<User> => user.followers
const getName = (user: User): string => user.name
// getFollowersNames: User -> ReadonlyArray<string>
const getFollowersNames = flow(getFollowers, map(getName))
// o se preferite usare `pipe` al posto di `flow`...
export const getFollowersNames2 = (user: User) =>
pipe(user, getFollowers, map(getName))
const user: User = {
id: 1,
name: 'Ruth R. Gonzalez',
followers: [
{ id: 2, name: 'Terry R. Emerson', followers: [] },
{ id: 3, name: 'Marsha J. Joslyn', followers: [] }
]
}
console.log(getFollowersNames(user)) // => [ 'Terry R. Emerson', 'Marsha J. Joslyn' ]Esempio (F = Option)
import { flow } from 'fp-ts/function'
import { none, Option, match, some } from 'fp-ts/Option'
// trasforma funzioni `B -> C` in funzioni `Option<B> -> Option<C>`
const map = <B, C>(g: (b: B) => C): ((fb: Option<B>) => Option<C>) =>
match(
() => none,
(b) => {
const c = g(b)
return some(c)
}
)
// -------------------
// esempio di utilizzo
// -------------------
import * as RA from 'fp-ts/ReadonlyArray'
const head: (input: ReadonlyArray<number>) => Option<number> = RA.head
const double = (n: number): number => n * 2
// getDoubleHead: ReadonlyArray<number> -> Option<number>
const getDoubleHead = flow(head, map(double))
console.log(getDoubleHead([1, 2, 3])) // => some(2)
console.log(getDoubleHead([])) // => noneEsempio (F = IO)
import { flow } from 'fp-ts/function'
import { IO } from 'fp-ts/IO'
// trasforma funzioni `B -> C` in funzioni `IO<B> -> IO<C>`
const map = <B, C>(g: (b: B) => C) => (fb: IO<B>): IO<C> => () => {
const b = fb()
return g(b)
}
// -------------------
// esempio di utilizzo
// -------------------
interface User {
readonly id: number
readonly name: string
}
// a dummy in memory database
const database: Record<number, User> = {
1: { id: 1, name: 'Ruth R. Gonzalez' },
2: { id: 2, name: 'Terry R. Emerson' },
3: { id: 3, name: 'Marsha J. Joslyn' }
}
const getUser = (id: number): IO<User> => () => database[id]
const getName = (user: User): string => user.name
// getUserName: number -> IO<string>
const getUserName = flow(getUser, map(getName))
console.log(getUserName(1)()) // => Ruth R. GonzalezEsempio (F = Task)
import { flow } from 'fp-ts/function'
import { Task } from 'fp-ts/Task'
// trasforma funzioni `B -> C` in funzioni `Task<B> -> Task<C>`
const map = <B, C>(g: (b: B) => C) => (fb: Task<B>): Task<C> => () => {
const promise = fb()
return promise.then(g)
}
// -------------------
// esempio di utilizzo
// -------------------
interface User {
readonly id: number
readonly name: string
}
// a dummy remote database
const database: Record<number, User> = {
1: { id: 1, name: 'Ruth R. Gonzalez' },
2: { id: 2, name: 'Terry R. Emerson' },
3: { id: 3, name: 'Marsha J. Joslyn' }
}
const getUser = (id: number): Task<User> => () => Promise.resolve(database[id])
const getName = (user: User): string => user.name
// getUserName: number -> Task<string>
const getUserName = flow(getUser, map(getName))
getUserName(1)().then(console.log) // => Ruth R. GonzalezEsempio (F = Reader)
import { flow } from 'fp-ts/function'
import { Reader } from 'fp-ts/Reader'
// trasforma funzioni `B -> C` in funzioni `Reader<R, B> -> Reader<R, C>`
const map = <B, C>(g: (b: B) => C) => <R>(fb: Reader<R, B>): Reader<R, C> => (
r
) => {
const b = fb(r)
return g(b)
}
// -------------------
// esempio di utilizzo
// -------------------
interface User {
readonly id: number
readonly name: string
}
interface Env {
// a dummy in memory database
readonly database: Record<string, User>
}
const getUser = (id: number): Reader<Env, User> => (env) => env.database[id]
const getName = (user: User): string => user.name
// getUserName: number -> Reader<Env, string>
const getUserName = flow(getUser, map(getName))
console.log(
getUserName(1)({
database: {
1: { id: 1, name: 'Ruth R. Gonzalez' },
2: { id: 2, name: 'Terry R. Emerson' },
3: { id: 3, name: 'Marsha J. Joslyn' }
}
})
) // => Ruth R. GonzalezPiù in generale, quando un certo type constructor F ammette una map che agisce in questo modo, diciamo che ammette una istanza di funtore.
Dal punto di vista matematico, i funtori sono delle mappe tra categorie che preservano la struttura categoriale, ovvero che preservano i morfismi identità e l'operazione di composizione.
Dato che le categorie sono costituite da due cose (gli oggetti e i morfismi) anche un funtore è costituito da due cose:
- una mappa tra oggetti che associa ad ogni oggetto
Xin C un oggettoF<X>in D - una mappa tra morfismi che associa ad ogni morfismo
fin C un morfismomap(f)in D
ove C e D sono due categorie (aka due linguaggi di programmazione).
Anche se una mappa tra due linguaggi di programmazione è un'idea intrigante, siamo più interessati ad una mappa in cui C and D coincidono (con la categoria TS). In questo caso parliamo di endofuntori ("endo" significa "dentro", "interno").
D'ora in poi, se non diversamente specificato, quando scrivo "funtore" intendo un endofuntore in TS.
Ora che sappiamo qual'è l'aspetto pratico che ci interessa dei funtori, vediamone la definizione formale.
Definizione. Un funtore è una coppia (F, map) ove:
Fè un type constructorn-ario (n >= 1) che mappa ogni tipoXin un tipoF<X>(mappa tra oggetti)mapè una funzione con la seguente firma:
map: <A, B>(f: (a: A) => B) => ((fa: F<A>) => F<B>)che mappa ciascuna funzione f: (a: A) => B in una funzione map(f): (fa: F<A>) => F<B> (mappa tra morfismi)
Devono valere le seguenti leggi:
map(1X)=1F(X) (le identità vanno in identità)map(g ∘ f) = map(g) ∘ map(f)(l'immagine di una composizione è la composizione delle immagini)
La seconda legge vi permette di rifattorizzare ottimizzando la computazione:
import { flow, increment, pipe } from 'fp-ts/function'
import { map } from 'fp-ts/ReadonlyArray'
const double = (n: number): number => n * 2
// cicla due volte
console.log(pipe([1, 2, 3], map(double), map(increment))) // => [ 3, 5, 7 ]
// cicla una volta sola
console.log(pipe([1, 2, 3], map(flow(double, increment)))) // => [ 3, 5, 7 ]I funtori hanno un impatto positivo sulla gestione degli errori funzionale, vediamo un esempio pratico:
declare const doSomethingWithIndex: (index: number) => string
export const program = (ns: ReadonlyArray<number>): string => {
// un risultato di -1 indica che nessun elemento è stato trovato
const i = ns.findIndex((n) => n > 0)
if (i !== -1) {
return doSomethingWithIndex(i)
}
throw new Error('cannot find a positive number')
}Usando l'API nativa findIndex per procedere con il flusso del programma occorre testare il risultato parziale con un if (sempre che ce ne ricordiamo! Il risultato di findIndex può essere inavvertitamente passato come input a doSomethingWithIndex).
Vediamo invece come si può ottenere più facilmente un risultato analogo usando Option e la sua istanza di funtore:
import { pipe } from 'fp-ts/function'
import { map, Option } from 'fp-ts/Option'
import { findIndex } from 'fp-ts/ReadonlyArray'
declare const doSomethingWithIndex: (index: number) => string
export const program = (ns: ReadonlyArray<number>): Option<string> =>
pipe(
ns,
findIndex((n) => n > 0),
map(doSomethingWithIndex)
)In pratica, utilizzando Option, abbiamo sempre di fronte l'happy path, la gestione dell'errore avviene dietro le quinte grazie alla sua map.
Quiz. Task<A> rappresenta una computazione asincrona che non può fallire, come possiamo modellare invece una computazione asincrona che può fallire?
I funtori compongono, ovvero dati due funtori F e G, allora la composizione F<G<A>> è ancora un funtore e la map della composizione è la composizione delle map.
Esempio (F = Task, G = Option)
import { flow } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
import * as T from 'fp-ts/Task'
type TaskOption<A> = T.Task<O.Option<A>>
export const map: <A, B>(
f: (a: A) => B
) => (fa: TaskOption<A>) => TaskOption<B> = flow(O.map, T.map)
// -------------------
// esempio di utilizzo
// -------------------
interface User {
readonly id: number
readonly name: string
}
// a dummy remote database
const database: Record<number, User> = {
1: { id: 1, name: 'Ruth R. Gonzalez' },
2: { id: 2, name: 'Terry R. Emerson' },
3: { id: 3, name: 'Marsha J. Joslyn' }
}
const getUser = (id: number): TaskOption<User> => () =>
Promise.resolve(O.fromNullable(database[id]))
const getName = (user: User): string => user.name
// getUserName: number -> TaskOption<string>
const getUserName = flow(getUser, map(getName))
getUserName(1)().then(console.log) // => some('Ruth R. Gonzalez')
getUserName(4)().then(console.log) // => nonePrima di procedere voglio mostrarvi una variante del concetto di funtore che abbiamo visto nella sezione precedente: i funtori controvarianti.
Ad essere pignoli infatti quelli che abbiamo chiamato semplicemente "funtori" dovrebbero essere più propriamente chiamati funtori covarianti.
La definizione di funtore controvariante è del tutto analoga a quella di funtore covariante, eccetto per la firma della sua operazione fondamentale (che viene chiamata contramap invece di map)
Esempio
import { map } from 'fp-ts/Option'
import { contramap } from 'fp-ts/Eq'
type User = {
readonly id: number
readonly name: string
}
const getId = (_: User): number => _.id
// come lavora `map`...
// const getIdOption: (fa: Option<User>) => Option<number>
const getIdOption = map(getId)
// come lavora `contramap`...
// const getIdEq: (fa: Eq<number>) => Eq<User>
const getIdEq = contramap(getId)
import * as N from 'fp-ts/number'
const EqID = getIdEq(N.Eq)
/*
Nel capitolo su `Eq` avevamo fatto:
const EqID: Eq<User> = pipe(
N.Eq,
contramap((_: User) => _.id)
)
*/Come facciamo a definire una istanza di funtore in fp-ts? Vediamo qualche esempio pratico.
La seguente dichiarazione definisce il modello di una risposta di una chiamata ad una API:
interface Response<A> {
readonly url: string
readonly status: number
readonly headers: Record<string, string>
readonly body: A
}Notate che il campo body è parametrico, questo fatto rende Response un buon candidato per cercare una istanza di funtore dato che Response è un type constructor n-ario con n >= 1 (una condizione necessaria).
Per poter definire una istanza di funtore per Response dobbiamo definire una funzione map insieme ad alcuni dettagli tecnici resi necessari da fp-ts.
// `Response.ts` module
import { pipe } from 'fp-ts/function'
import { Functor1 } from 'fp-ts/Functor'
declare module 'fp-ts/HKT' {
interface URItoKind<A> {
readonly Response: Response<A>
}
}
export interface Response<A> {
readonly url: string
readonly status: number
readonly headers: Record<string, string>
readonly body: A
}
export const map = <A, B>(f: (a: A) => B) => (
fa: Response<A>
): Response<B> => ({
...fa,
body: f(fa.body)
})
// functor instance for `Response<A>`
export const Functor: Functor1<'Response'> = {
URI: 'Response',
map: (fa, f) => pipe(fa, map(f))
}Non ancora. I funtori ci permettono di comporre un programma con effetti f con un programma puro g, ma g deve essere una funzione unaria, ovvero una funzione che accetta un solo argomento. Cosa succede se g accetta due o più argomenti?
| Program f | Program g | Composition |
|---|---|---|
| pure | pure | g ∘ f |
| effectful | pure (unary) | map(g) ∘ f |
| effectful | pure (n-ary, n > 1) |
? |
Per poter gestire questa circostanza abbiamo bisogno di qualcosa in più, nel prossimo capitolo vedremo un'altra importante astrazione della programmazione funzionale: i funtori applicativi.
Nella sezione riguardante i funtori abbiamo visto che possiamo comporre un programma con effetti f: (a: A) => F<B> con un programma puro g: (b: B) => C tramite una trasformazione di g in una funzione map(g): (fb: F<B>) => F<C>, ammesso che F ammetta una istanza di funtore.
| Program f | Program g | Composition |
|---|---|---|
| pure | pure | g ∘ f |
| effectful | pure (unary) | map(g) ∘ f |
Tuttavia g deve essere unaria, ovvero deve accettare un solo parametro in input. Che succede se g accetta due parametri? Possiamo ancora trasformare g usando solo l'istanza di funtore?
Prima di tutto dobbiamo modellare una funzione che accetta due parametri, diciamo di tipo B e C e restituisce un valore di tipo D:
g: (b: B, c: C) => DPossiamo riscrivere g usando una tecnica chiamata currying.
Currying is the technique of translating the evaluation of a function that takes multiple parameters into evaluating a sequence of functions, each with a single parameter. For example, a function that takes two parameters, one from
Band one fromC, and produces outputs inD, by currying is translated into a function that takes a single parameter fromBand produces as outputs functions fromCtoD.
(source: currying on wikipedia.org)
Perciò, tramite currying, possiamo riscrivere g come:
g: (b: B) => (c: C) => DEsempio
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const addFollower = (follower: User, user: User): User => ({
...user,
followers: [...user.followers, follower]
})Riscriviamo addFollower tramite currying
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const addFollower = (follower: User) => (user: User): User => ({
...user,
followers: [...user.followers, follower]
})
// -------------------
// esempio di utilizzo
// -------------------
const user: User = { id: 1, name: 'Ruth R. Gonzalez', followers: [] }
const follower: User = { id: 3, name: 'Marsha J. Joslyn', followers: [] }
console.log(addFollower(follower)(user))
/*
{
id: 1,
name: 'Ruth R. Gonzalez',
followers: [ { id: 3, name: 'Marsha J. Joslyn', followers: [] } ]
}
*/Ora supponiamo:
- di non avere a disposizione
followerma solo il suoid - di non avere a disposizione
userma solo il suoid - di avere a disposizione una API
fetchUserche, dato unid, contatta un endpoint che restituisce loUsercorrispondente
import * as T from 'fp-ts/Task'
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const addFollower = (follower: User) => (user: User): User => ({
...user,
followers: [...user.followers, follower]
})
declare const fetchUser: (id: number) => T.Task<User>
const userId = 1
const followerId = 3
const result = addFollower(fetchUser(followerId))(fetchUser(userId)) // non compila!Non posso più usare addFollower! Come possiamo procedere?
Se avessimo a disposizione una funzione con la seguente firma:
declare const addFollowerAsync: (
follower: T.Task<User>
) => (user: T.Task<User>) => T.Task<User>potremmo procedere comodamente:
import * as T from 'fp-ts/Task'
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
declare const fetchUser: (id: number) => T.Task<User>
declare const addFollowerAsync: (
follower: T.Task<User>
) => (user: T.Task<User>) => T.Task<User>
const userId = 1
const followerId = 3
// const result: T.Task<User>
const result = addFollowerAsync(fetchUser(followerId))(fetchUser(userId)) // ora compilaPossiamo naturalmente provare ad implementare manualmente addFollowerAsync, ma è possibile invece trovare una trasformazione che partendo da una funzione come addFollower: (follower: User) => (user: User): User restituisca una funzione come addFollowerAsync: (follower: Task<User>) => (user: Task<User>) => Task<User>?
Più in generale quello che vorremmo è una trasformazione, chiamiamola liftA2, che partendo da una funzione g: (b: B) => (c: C) => D restituisca una funzione con la seguente firma:
liftA2(g): (fb: F<B>) => (fc: F<C>) => F<D>Come facciamo ad ottenerla? Siccome adesso g è unaria, possiamo usare l'istanza di funtore e la nostra vecchia map:
map(g): (fb: F<B>) => F<(c: C) => D>Ma ora siamo bloccati: non c'è alcuna operazione legale fornita dall'istanza di funtore che ci permette di "spacchettare" il tipo F<(c: C) => D> nel tipo (fc: F<C>) => F<D>.
Introduciamo perciò una nuova operazione ap che realizza questo spacchettamento:
declare const ap: <A>(fa: Task<A>) => <B>(fab: Task<(a: A) => B>) => Task<B>Nota. Come mai il nome "ap"? Perché può essere vista come una sorta di applicazione di funzione
// `apply` applica una funzione ad un valore
declare const apply: <A>(a: A) => <B>(f: (a: A) => B) => B
declare const ap: <A>(a: Task<A>) => <B>(f: Task<(a: A) => B>) => Task<B>
// `ap` applica una funzione racchiusa in un effetto ad un valore racchiuso in un effettoOra, data l'operazione ap possiamo definire liftA2:
import { pipe } from 'fp-ts/function'
import * as T from 'fp-ts/Task'
const liftA2 = <B, C, D>(g: (b: B) => (c: C) => D) => (fb: T.Task<B>) => (
fc: T.Task<C>
): T.Task<D> => pipe(fb, T.map(g), T.ap(fc))
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const addFollower = (follower: User) => (user: User): User => ({
...user,
followers: [...user.followers, follower]
})
// const addFollowerAsync: (fb: T.Task<User>) => (fc: T.Task<User>) => T.Task<User>
const addFollowerAsync = liftA2(addFollower)e infine, comporre fetchUser con il risultato precedente:
import { flow, pipe } from 'fp-ts/function'
import * as T from 'fp-ts/Task'
const liftA2 = <B, C, D>(g: (b: B) => (c: C) => D) => (fb: T.Task<B>) => (
fc: T.Task<C>
): T.Task<D> => pipe(fb, T.map(g), T.ap(fc))
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const addFollower = (follower: User) => (user: User): User => ({
...user,
followers: [...user.followers, follower]
})
declare const fetchUser: (id: number) => T.Task<User>
// const program: (id: number) => (fc: T.Task<User>) => T.Task<User>
const program = flow(fetchUser, liftA2(addFollower))
const userId = 1
const followerId = 3
// const result: T.Task<User>
const result = program(followerId)(fetchUser(userId))Abbiamo trovato una procedura standard per comporre due funzioni f: (a: A) => F<B>, g: (b: B, c: C) => D:
- si trasforma
gtramite currying in una funzioneg: (b: B) => (c: C) => D - si definisce la funzione
apper l'effettoF(funzione di libreria) - si definisce la funzione di utility
liftA2per l'effettoF(funzione di libreria) - si ottiene la composizione con
flow(f, liftA2(g))
Vediamo come è definita l'opererazione ap per alcuni type constructor già noti:
Esempio (F = ReadonlyArray)
import { increment, pipe } from 'fp-ts/function'
const ap = <A>(fa: ReadonlyArray<A>) => <B>(
fab: ReadonlyArray<(a: A) => B>
): ReadonlyArray<B> => {
const out: Array<B> = []
for (const f of fab) {
for (const a of fa) {
out.push(f(a))
}
}
return out
}
const double = (n: number): number => n * 2
pipe([double, increment], ap([1, 2, 3]), console.log) // => [ 2, 4, 6, 2, 3, 4 ]Esempio (F = Option)
import { pipe } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
const ap = <A>(fa: O.Option<A>) => <B>(
fab: O.Option<(a: A) => B>
): O.Option<B> =>
pipe(
fab,
O.match(
() => O.none,
(f) =>
pipe(
fa,
O.match(
() => O.none,
(a) => O.some(f(a))
)
)
)
)
const double = (n: number): number => n * 2
pipe(O.some(double), ap(O.some(1)), console.log) // => some(2)
pipe(O.some(double), ap(O.none), console.log) // => none
pipe(O.none, ap(O.some(1)), console.log) // => none
pipe(O.none, ap(O.none), console.log) // => noneEsempio (F = IO)
import { IO } from 'fp-ts/IO'
const ap = <A>(fa: IO<A>) => <B>(fab: IO<(a: A) => B>): IO<B> => () => {
const f = fab()
const a = fa()
return f(a)
}Esempio (F = Task)
import { Task } from 'fp-ts/Task'
const ap = <A>(fa: Task<A>) => <B>(fab: Task<(a: A) => B>): Task<B> => () =>
Promise.all([fab(), fa()]).then(([f, a]) => f(a))Esempio (F = Reader)
import { Reader } from 'fp-ts/Reader'
const ap = <R, A>(fa: Reader<R, A>) => <B>(
fab: Reader<R, (a: A) => B>
): Reader<R, B> => (r) => {
const f = fab(r)
const a = fa(r)
return f(a)
}Abbiamo visto che con ap possiamo gestire funzioni con due parametri, ma che succede con le funzioni che accettano tre parametri? Abbiamo bisogno di un'altra astrazione ancora?
La buona notizia è che la risposta è no, map + ap sono sufficienti:
import { pipe } from 'fp-ts/function'
import * as T from 'fp-ts/Task'
const liftA3 = <B, C, D, E>(f: (b: B) => (c: C) => (d: D) => E) => (
fb: T.Task<B>
) => (fc: T.Task<C>) => (fd: T.Task<D>): T.Task<E> =>
pipe(fb, T.map(f), T.ap(fc), T.ap(fd))
const liftA4 = <B, C, D, E, F>(
f: (b: B) => (c: C) => (d: D) => (e: E) => F
) => (fb: T.Task<B>) => (fc: T.Task<C>) => (fd: T.Task<D>) => (
fe: T.Task<E>
): T.Task<F> => pipe(fb, T.map(f), T.ap(fc), T.ap(fd), T.ap(fe))
// etc...Ora possiamo aggiornare la nostra "tabella di composizione":
| Program f | Program g | Composition |
|---|---|---|
| pure | pure | g ∘ f |
| effectful | pure (unary) | map(g) ∘ f |
| effectful | pure, n-ary |
liftAn(g) ∘ f |
Ora sappiamo che se abbiamo due funzioni f: (a: A) => F<B>, g: (b: B, c: C) => D possiamo ottenerne la composizione h:
h: (a: A) => (fc: F<C>) => F<D>Per eseguire h abbiamo perciò bisogno di un valore di tipo A e di un valore di tipo F<C>.
Ma che succede se invece di un valore di tipo F<C> per il secondo parametro fc abbiamo a disposizione solo un valore di tipo C?
Sarebbe utile un'operazione che sia in grado di trasformare un valore di tipo C in un valore di tipo F<C>, in modo che si possa poi usare h.
Introduciamo perciò una tale operazione, chiamata of (possibili sinonimi pure, return):
declare const of: <C>(c: C) => F<C>In letteratura si parla di funtori applicativi per i type constructor che ammettono, in aggiunta a map, ambedue le operazioni ap e of.
Vediamo come è definita l'opererazione of per alcuni type constructor noti:
Esempio (F = ReadonlyArray)
const of = <A>(a: A): ReadonlyArray<A> => [a]Esempio (F = Option)
import * as O from 'fp-ts/Option'
const of = <A>(a: A): O.Option<A> => O.some(a)Esempio (F = IO)
import { IO } from 'fp-ts/IO'
const of = <A>(a: A): IO<A> => () => aEsempio (F = Task)
import { Task } from 'fp-ts/Task'
const of = <A>(a: A): Task<A> => () => Promise.resolve(a)Esempio (F = Reader)
import { Reader } from 'fp-ts/Reader'
const of = <R, A>(a: A): Reader<R, A> => () => aI funtori applicativi compongono, ovvero dati due funtori applicativi F e G, la loro composizione F<G<A>> è ancora un funtore applicativo.
Esempio (F = Task, G = Option)
La of della composizione è la composizione delle of:
import { flow } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
import * as T from 'fp-ts/Task'
type TaskOption<A> = T.Task<O.Option<A>>
const of: <A>(a: A) => TaskOption<A> = flow(O.of, T.of)la ap della composizione si ottiene dal seguente pattern:
const ap = <A>(
fa: TaskOption<A>
): (<B>(fab: TaskOption<(a: A) => B>) => TaskOption<B>) =>
flow(
T.map((gab) => (ga: O.Option<A>) => O.ap(ga)(gab)),
T.ap(fa)
)Non ancora. C'è ancora un ultimo importante caso da considerare: quando entrambi i programmi sono con effetti.
Ancora una volta abbiamo bisogno di qualche cosa in più, nel capitolo seguente parleremo di una delle astrazioni più importanti in programmazione funzionale: le monadi.
(Eugenio Moggi is a professor of computer science at the University of Genoa, Italy. He first described the general use of monads to structure programs)
(Philip Lee Wadler is an American computer scientist known for his contributions to programming language design and type theory)
Nell'ultimo capitolo abbiamo visto che possiamo comporre un programma con effetti f: (a: A) => F<B> con un programma n-ario puro g, ammesso che F ammetta una istanza di funtore applicativo:
| Program f | Program g | Composition |
|---|---|---|
| pure | pure | g ∘ f |
| effectful | pure (unary) | map(g) ∘ f |
| effectful | pure, n-ary |
liftAn(g) ∘ f |
Tuttavia dobbiamo risolvere un ultimo (e frequente) caso: quando entrambi i programmi sono con effetto:
f: (a: A) => F<B>
g: (b: B) => F<C>Qual'è la composizione di f e g?
Per mostrare meglio perché abbiamo bisogno di qualcosa in più, vediamo qualche esempio.
Esempio (F = Array)
Supponiamo di voler ricavare i follower dei follower:
import { pipe } from 'fp-ts/function'
import * as A from 'fp-ts/ReadonlyArray'
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const getFollowers = (user: User): ReadonlyArray<User> => user.followers
declare const user: User
// followersOfFollowers: ReadonlyArray<ReadonlyArray<User>>
const followersOfFollowers = pipe(user, getFollowers, A.map(getFollowers))C'è qualcosa che non va, followersOfFollowers ha tipo ReadonlyArray<ReadonlyArray<User>> ma noi vorremmo ReadonlyArray<User>.
Abbiamo bisogno di appiattire (flatten) gli array innestati.
La funzione flatten: <A>(mma: ReadonlyArray<ReadonlyArray<A>>) => ReadonlyArray<A> esportata dal modulo fp-ts/ReadonlyArray fa al caso nostro:
// followersOfFollowers: ReadonlyArray<User>
const followersOfFollowers = pipe(
user,
getFollowers,
A.map(getFollowers),
A.flatten
)Bene! Vediamo con un'altra struttura dati.
Esempio (F = Option)
Supponiamo di voler calcolare il reciproco del primo elemento di un array numerico:
import { pipe } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
import * as A from 'fp-ts/ReadonlyArray'
const inverse = (n: number): O.Option<number> =>
n === 0 ? O.none : O.some(1 / n)
// inverseHead: O.Option<O.Option<number>>
const inverseHead = pipe([1, 2, 3], A.head, O.map(inverse))Opss, è successo di nuovo, inverseHead ha tipo Option<Option<number>> ma noi vogliamo Option<number>.
Abbiamo bisogno di appiattire le Option innestate.
La funzione flatten: <A>(mma: Option<Option<A>>) => Option<A> esportata dal modulo fp-ts/Option fa al caso nostro:
// inverseHead: O.Option<number>
const inverseHead = pipe([1, 2, 3], A.head, O.map(inverse), O.flatten)Tutte quelle funzioni flatten... Non sono una coincidenza, c'è un pattern funzionale dietro le quinte: ambedue i type constructor ReadonlyArray e Option (e molti altri) ammettono una istanza di monade e
flattenis the most peculiar operation of monads
Nota. Un possibile sinonimo di flatten è join.
Dunque cos'è una monade?
Ecco come spesso sono presentate...
Definizione. Una monade è definita da tre cose:
(1) un type constructor M che ammette una istanza di funtore
(2) una funzione of (possibili sinonimi pure, return) con la seguente firma:
of: <A>(a: A) => M<A>(3) una funzione chain (possibili sinonimi flatMap, bind) con la seguente firma:
chain: <A, B>(f: (a: A) => M<B>) => (ma: M<A>) => M<B>Le funzioni of e chain devono obbedire a tre leggi:
chain(of) ∘ f = f(Left identity)chain(f) ∘ of = f(Right identity)chain(h) ∘ (chain(g) ∘ f) = chain((chain(h) ∘ g)) ∘ f(Associativity)
ove f, g, h sono tutte funzioni con effetto M e ∘ è l'usuale composizione di funzioni.
Dopo aver visto per la prima volta questa definizione avevo in testa molte domande:
- perché proprio quelle due operazioni
ofechain? e perché hanno quella firma? - come mai i sinonimi "pure" e "flatMap"?
- perché devono valere quelle leggi? Che cosa significano?
- come mai se
flattenè così importante per le monadi non compare nella sua definizione?
Questo capitolo cercherà di rispondere a tutte queste domande.
Ora torniamo al nostro problema centrale: che cos'è la composizione di due funzioni f e g con effetto?
Nota. Una funzione con effetto è anche chiamata Kleisli arrow.
Per ora non so nemmeno che tipo abbia una tale composizione.
Un momento... abbiamo già incontrato una astrazione che parla specificatamente di composizione. Vi ricordate cosa ho detto a proposito delle categorie?
Categories capture the essence of composition
Possiamo trasformare il nostro problema in un problema categoriale, ovvero: possiamo trovare una categoria che modella la composizione delle Kleisli arrows?
(Heinrich Kleisli, Swiss mathematician)
Cerchiamo di costruire una categoria K (chiamata categoria di Kleisli) che contenga solo Kleisli arrow:
- gli oggetti sono gli stessi oggetti della categoria TS, ovvero tutti i tipi di TypeScript.
- i morfismi sono costruiti così: ogni volta che c'è una Kleisli arrow
f: A ⟼ M<B>in TS tracciamo una frecciaf': A ⟼ Bin K
(sopra la categoria TS, sotto la costruzione di K)
Dunque cosa sarebbe la composizione di f e g in K? E' la freccia rossa chiamata h' nell'immagine qui sotto:
(sopra la categoria TS, sotto la costruzione di K)
Dato che h' è una freccia che va da A a C in K, possiamo far corrispondere una funzione h che va da A a M<C> in TS.
Quindi un buon candidato per la composizione di f e g in TS è ancora una Kleisli arrow con la seguente firma: (a: A) => M<C>.
Come facciamo a costruire concretamente una tale funzione? Beh, proviamoci!
Il punto (1) della definizione di monade ci dice che M ammette una istanza di funtore, percò possiamo usare map per trasformare la funzione g: (b: B) => M<C> in una funzione map(g): (mb: M<B>) => M<M<C>>
(come ottenere la funzione h)
Ma ora siamo bloccati: non c'è alcuna operazione legale della istanza di funtore che ci permette di appiattire un valore di tipo M<M<C>> in un valore di tipo M<C>, abbiamo bisogno di una operazione addizionale, chiamiamola flatten.
Se riusciamo a definire una tale operazione allora possiamo ottenere la composizione che stavamo cercando:
h = flatten ∘ map(g) ∘ f
Ma aspettate... contraendo flatten ∘ map(g) otteniamo "flatMap", ecco da dove viene il nome!
Dunque possiamo ottenere chain in questo modo
chain = flatten ∘ map(g)
(come agisce chain sulla funzione g)
Ora possiamo aggiornare la nostra "tabella di composizione"
| Program f | Program g | Composition |
|---|---|---|
| pure | pure | g ∘ f |
| effectful | pure (unary) | map(g) ∘ f |
| effectful | pure, n-ary |
liftAn(g) ∘ f |
| effectful | effectful | chain(g) ∘ f |
E per quanto riguarda l'operazione of? Ebbene, of proviene dai morfismi identità in K: per ogni morfismo identità 1A in K deve esserci una corrispondente funzione da A a M<A> (ovvero of: <A>(a: A) => M<A>).
(come ottenere of)
Il fatto che la of sia l'elemento neutro rispetto alla chain permette questo tipo di controllo di flusso (piuttosto comune):
pipe(
mb,
M.chain((b) => (predicate(b) ? M.of(b) : g(b)))
)ove predicate: (b: B) => boolean, mb: M<B> e g: (b: B) => M<B>.
Ultima domanda: da dove nascono le leggi? Esse non sono altro che le leggi categoriali in K tradotte in TS:
| Law | K | TS |
|---|---|---|
| Left identity | 1B ∘ f' = f' |
chain(of) ∘ f = f |
| Right identity | f' ∘ 1A = f' |
chain(f) ∘ of = f |
| Associativity | h' ∘ (g' ∘ f') = (h' ∘ g') ∘ f' |
chain(h) ∘ (chain(g) ∘ f) = chain((chain(h) ∘ g)) ∘ f |
Se adesso torniamo agli esempi che mostravano il problema con i contesti innestati possiamo risolverli usando chain:
import { pipe } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
import * as A from 'fp-ts/ReadonlyArray'
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const getFollowers = (user: User): ReadonlyArray<User> => user.followers
declare const user: User
const followersOfFollowers: ReadonlyArray<User> = pipe(
user,
getFollowers,
A.chain(getFollowers)
)
const inverse = (n: number): O.Option<number> =>
n === 0 ? O.none : O.some(1 / n)
const inverseHead: O.Option<number> = pipe([1, 2, 3], A.head, O.chain(inverse))Vediamo come è definita l'opererazione chain per alcuni type constructor noti:
Esempio (F = ReadonlyArray)
// trasforma funzioni `B -> ReadonlyArray<C>` in funzioni `ReadonlyArray<B> -> ReadonlyArray<C>`
const chain = <B, C>(g: (b: B) => ReadonlyArray<C>) => (
mb: ReadonlyArray<B>
): ReadonlyArray<C> => {
const out: Array<C> = []
for (const b of mb) {
out.push(...g(b))
}
return out
}Esempio (F = Option)
import { match, none, Option } from 'fp-ts/Option'
// trasforma funzioni `B -> Option<C>` in funzioni `Option<B> -> Option<C>`
const chain = <B, C>(g: (b: B) => Option<C>): ((mb: Option<B>) => Option<C>) =>
match(() => none, g)Esempio (F = IO)
import { IO } from 'fp-ts/IO'
// trasforma funzioni `B -> IO<C>` in funzioni `IO<B> -> IO<C>`
const chain = <B, C>(g: (b: B) => IO<C>) => (mb: IO<B>): IO<C> => () =>
g(mb())()Esempio (F = Task)
import { Task } from 'fp-ts/Task'
// trasforma funzioni `B -> Task<C>` in funzioni `Task<B> -> Task<C>`
const chain = <B, C>(g: (b: B) => Task<C>) => (mb: Task<B>): Task<C> => () =>
mb().then((b) => g(b)())Esempio (F = Reader)
import { Reader } from 'fp-ts/Reader'
// trasforma funzioni `B -> Reader<R, C>` in funzioni `Reader<R, B> -> Reader<R, C>`
const chain = <B, R, C>(g: (b: B) => Reader<R, C>) => (
mb: Reader<R, B>
): Reader<R, C> => (r) => g(mb(r))(r)Vediamo ora come, grazie alla trasparenza referenziale e al concetto di monade, possiamo manipolare i programmi programmaticamente.
Ecco un piccolo programma che legge / scrive su un file:
import { log } from 'fp-ts/Console'
import { IO, chain } from 'fp-ts/IO'
import { pipe } from 'fp-ts/function'
import * as fs from 'fs'
// -----------------------------------------
// funzioni di libreria
// -----------------------------------------
const readFile = (filename: string): IO<string> => () =>
fs.readFileSync(filename, 'utf-8')
const writeFile = (filename: string, data: string): IO<void> => () =>
fs.writeFileSync(filename, data, { encoding: 'utf-8' })
// API derivata dalle precedenti
const modifyFile = (filename: string, f: (s: string) => string): IO<void> =>
pipe(
readFile(filename),
chain((s) => writeFile(filename, f(s)))
)
// -----------------------------------------
// programma
// -----------------------------------------
const program1 = pipe(
readFile('file.txt'),
chain(log),
chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
chain(() => readFile('file.txt')),
chain(log)
)L'azione:
pipe(readFile('file.txt'), chain(log))è ripetuta due volte nel programma, ma dato che vale la trasparenza referenziale possiamo mettere a fattor comune l'azione assegnandola ad una costante:
const read = pipe(readFile('file.txt'), chain(log))
const modify = modifyFile('file.txt', (s) => s + '\n// eof')
const program2 = pipe(
read,
chain(() => modify),
chain(() => read)
)Possiamo persino definire un combinatore e sfruttarlo per rendere più compatto il codice:
const interleave = <A, B>(action: IO<A>, middle: IO<B>): IO<A> =>
pipe(
action,
chain(() => middle),
chain(() => action)
)
const program3 = interleave(read, modify)Un altro esempio: implementare una funzione simile a time di Unix (la parte relativa al tempo di esecuzione reale) per IO.
import * as IO from 'fp-ts/IO'
import { now } from 'fp-ts/Date'
import { log } from 'fp-ts/Console'
import { pipe } from 'fp-ts/function'
// logga la durata in millisecondi della computazione
export const time = <A>(ma: IO.IO<A>): IO.IO<A> =>
pipe(
now,
IO.chain((startMillis) =>
pipe(
ma,
IO.chain((a) =>
pipe(
now,
IO.chain((endMillis) =>
pipe(
log(`Elapsed: ${endMillis - startMillis}`),
IO.map(() => a)
)
)
)
)
)
)
)Excursus. Come potete osservare, usare chain quando occorre mantenere uno scope porta a scrivere codice verboso.
Nei linguaggi che supportano nativamente lo stile monadico esistono solitamente dei costrutti sintattici che
vanno sotto il nome di "do notation" e che agevolano questo tipo di situazione.
Vediamo un esempio in Haskell
now :: IO Int
now = undefined -- usare `undefined` è l'equivalente Haskell di usare `declare` in TypeScript
log :: String -> IO ()
log = undefined
time :: IO a -> IO a
time ma = do
startMillis <- now
a <- ma
endMillis <- now
log ("Elapsed:" ++ show (endMillis - startMillis))
return aIn TypeScript non abbiamo alcun costrutto del genere, ma si può simulare qualcosa di simile:
import { log } from 'fp-ts/Console'
import { now } from 'fp-ts/Date'
import { pipe } from 'fp-ts/function'
import * as IO from 'fp-ts/IO'
// logga la durata in millisecondi della computazione
export const time = <A>(ma: IO.IO<A>): IO.IO<A> =>
pipe(
IO.Do,
IO.bind('startMillis', () => now),
IO.bind('a', () => ma),
IO.bind('endMillis', () => now),
IO.chainFirst(({ endMillis, startMillis }) =>
log(`Elapsed: ${endMillis - startMillis}`)
),
IO.map(({ a }) => a)
)Ora vediamo un esempio di utilizzo del combinatore time:
import { randomInt } from 'fp-ts/Random'
import { Monoid, concatAll } from 'fp-ts/Monoid'
import { replicate } from 'fp-ts/ReadonlyArray'
const fib = (n: number): number => (n <= 1 ? 1 : fib(n - 1) + fib(n - 2))
// lancia `fib` con un intero causuale tra 30 e 35
// e logga sia l'input che l'output
const randomFib: IO.IO<void> = pipe(
randomInt(30, 35),
IO.chain((n) => log([n, fib(n)]))
)
// una istanza di monoide per `IO<void>`
const MonoidIO: Monoid<IO.IO<void>> = {
concat: (first, second) => () => {
first()
second()
},
empty: IO.of(undefined)
}
// esegue `n` volte la computazione `mv`
const replicateIO = (n: number, mv: IO.IO<void>): IO.IO<void> =>
concatAll(MonoidIO)(replicate(n, mv))
// -------------------
// esempio di utilizzo
// -------------------
time(replicateIO(3, randomFib))()
/*
[ 31, 2178309 ]
[ 33, 5702887 ]
[ 30, 1346269 ]
Elapsed: 89
*/Stampando anche i parziali
time(replicateIO(3, time(randomFib)))()
/*
[ 33, 5702887 ]
Elapsed: 54
[ 30, 1346269 ]
Elapsed: 13
[ 32, 3524578 ]
Elapsed: 39
Elapsed: 106
*/Una cosa interessante di lavorare con l'interfaccia monadica (map, of, chain) è la possibilità di poter iniettare le dipendenze di cui ha bisogno il programma, ivi compreso il modo per concatenare le diverse computazioni.
Per vederlo riprendiamo il piccolo programma che legge e scrive su file e operiamo il seguente refactoring:
import { IO } from 'fp-ts/IO'
import { pipe } from 'fp-ts/function'
// -----------------------------------------
// dipendenze (una "port" nella nomenclatura della Hexagonal Architecture)
// -----------------------------------------
interface Deps {
readonly readFile: (filename: string) => IO<string>
readonly writeFile: (filename: string, data: string) => IO<void>
readonly log: <A>(a: A) => IO<void>
readonly chain: <A, B>(f: (a: A) => IO<B>) => (ma: IO<A>) => IO<B>
}
// -----------------------------------------
// programma
// -----------------------------------------
const program4 = (D: Deps) => {
const modifyFile = (filename: string, f: (s: string) => string) =>
pipe(
D.readFile(filename),
D.chain((s) => D.writeFile(filename, f(s)))
)
return pipe(
D.readFile('file.txt'),
D.chain(D.log),
D.chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
D.chain(() => D.readFile('file.txt')),
D.chain(D.log)
)
}
// -----------------------------------------
// istanza per `Deps` (un "adapter" nella nomenclatura della Hexagonal Architecture)
// -----------------------------------------
import * as fs from 'fs'
import { log } from 'fp-ts/Console'
import { chain } from 'fp-ts/IO'
const DepsSync: Deps = {
readFile: (filename) => () => fs.readFileSync(filename, 'utf-8'),
writeFile: (filename: string, data: string) => () =>
fs.writeFileSync(filename, data, { encoding: 'utf-8' }),
log,
chain
}
// dependency injection
program4(DepsSync)()L'istanza DepsSync è quella di "produzione" (legge e scrive sul vero filesystem), ma è relativamente semplice definirne una adatta a verificare il comportamento del programma e a scrivere test:
import { log } from 'fp-ts/Console'
import { chain, of } from 'fp-ts/IO'
// istanza di test
const DepsTest: Deps = {
readFile: (filename) =>
pipe(
log(`calling readFile(${filename})...`),
chain(() => of('content'))
),
writeFile: (filename: string, data: string) =>
log(`calling writeFile(${filename}, ${data})...`),
log: (message) => log(`calling log(${message})...`),
chain
}
program4(DepsTest)()
/*
calling readFile(file.txt)...
calling log(content)...
calling readFile(file.txt)...
calling writeFile(file.txt, content
// eof)...
calling readFile(file.txt)...
calling log(content)...
*/Ma c'è di più, possiamo persino astrarre l'effetto in cui gira il programma. Definiamo un nostro effetto FileSystem (l'effetto di leggere / scrivere sul file system):
import { IO } from 'fp-ts/IO'
import { pipe } from 'fp-ts/function'
// -----------------------------------------
// effetto del nostro programma
// -----------------------------------------
interface FileSystem<A> extends IO<A> {}
// -----------------------------------------
// dipendenze
// -----------------------------------------
interface Deps {
readonly readFile: (filename: string) => FileSystem<string>
readonly writeFile: (filename: string, data: string) => FileSystem<void>
readonly log: <A>(a: A) => FileSystem<void>
readonly chain: <A, B>(
f: (a: A) => FileSystem<B>
) => (ma: FileSystem<A>) => FileSystem<B>
}
// -----------------------------------------
// programma
// -----------------------------------------
const program4 = (D: Deps) => {
const modifyFile = (filename: string, f: (s: string) => string) =>
pipe(
D.readFile(filename),
D.chain((s) => D.writeFile(filename, f(s)))
)
return pipe(
D.readFile('file.txt'),
D.chain(D.log),
D.chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
D.chain(() => D.readFile('file.txt')),
D.chain(D.log)
)
}Ora, con un semplice cambiamento nella definizione dell'effetto FileSystem, possiamo modificare il programma in modo che possa girare in un contesto asincrono:
// -----------------------------------------
// effetto del nostro programma
// -----------------------------------------
-interface FileSystem<A> extends IO<A> {}
+interface FileSystem<A> extends Task<A> {}dopodichè non ci resta che modificare l'istanza per Deps per adattarsi alla nuova definizione:
import { Task } from 'fp-ts/Task'
import { pipe } from 'fp-ts/function'
// -----------------------------------------
// effetto del nostro programma (modificato)
// -----------------------------------------
interface FileSystem<A> extends Task<A> {}
// -----------------------------------------
// dipendenze (NON modificato)
// -----------------------------------------
interface Deps {
readonly readFile: (filename: string) => FileSystem<string>
readonly writeFile: (filename: string, data: string) => FileSystem<void>
readonly log: <A>(a: A) => FileSystem<void>
readonly chain: <A, B>(
f: (a: A) => FileSystem<B>
) => (ma: FileSystem<A>) => FileSystem<B>
}
// -----------------------------------------
// programma (NON modificato)
// -----------------------------------------
const program5 = (D: Deps) => {
const modifyFile = (filename: string, f: (s: string) => string) =>
pipe(
D.readFile(filename),
D.chain((s) => D.writeFile(filename, f(s)))
)
return pipe(
D.readFile('file.txt'),
D.chain(D.log),
D.chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
D.chain(() => D.readFile('file.txt')),
D.chain(D.log)
)
}
// -----------------------------------------
// istanza per `Deps` (modificato)
// -----------------------------------------
import * as fs from 'fs'
import { log } from 'fp-ts/Console'
import { chain, fromIO } from 'fp-ts/Task'
const DepsAsync: Deps = {
readFile: (filename) => () =>
new Promise((resolve) =>
fs.readFile(filename, { encoding: 'utf-8' }, (_, s) => resolve(s))
),
writeFile: (filename: string, data: string) => () =>
new Promise((resolve) => fs.writeFile(filename, data, () => resolve())),
log: (a) => fromIO(log(a)),
chain
}
// dependency injection
program5(DepsAsync)()Quiz. Gli esempi precedenti non tengono conto (volontariamente) di possibili errori (per esempio il fatto che non esista il file da cui leggiamo), come si potrebbe modificare l'effetto FileSystem per tenerne conto?
import { Task } from 'fp-ts/Task'
import { pipe } from 'fp-ts/function'
import * as E from 'fp-ts/Either'
// -----------------------------------------
// effetto del nostro programma (modificato)
// -----------------------------------------
interface FileSystem<A> extends Task<E.Either<Error, A>> {}
// -----------------------------------------
// dipendenze (NON modificato)
// -----------------------------------------
interface Deps {
readonly readFile: (filename: string) => FileSystem<string>
readonly writeFile: (filename: string, data: string) => FileSystem<void>
readonly log: <A>(a: A) => FileSystem<void>
readonly chain: <A, B>(
f: (a: A) => FileSystem<B>
) => (ma: FileSystem<A>) => FileSystem<B>
}
// -----------------------------------------
// programma (NON modificato)
// -----------------------------------------
const program5 = (D: Deps) => {
const modifyFile = (filename: string, f: (s: string) => string) =>
pipe(
D.readFile(filename),
D.chain((s) => D.writeFile(filename, f(s)))
)
return pipe(
D.readFile('-.txt'),
D.chain(D.log),
D.chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
D.chain(() => D.readFile('file.txt')),
D.chain(D.log)
)
}
// -----------------------------------------
// istanza per `Deps` (modificato)
// -----------------------------------------
import * as fs from 'fs'
import { log } from 'fp-ts/Console'
import { chain, fromIO } from 'fp-ts/TaskEither'
const DepsAsync: Deps = {
readFile: (filename) => () =>
new Promise((resolve) =>
fs.readFile(filename, { encoding: 'utf-8' }, (err, s) => {
if (err !== null) {
resolve(E.left(err))
} else {
resolve(E.right(s))
}
})
),
writeFile: (filename: string, data: string) => () =>
new Promise((resolve) =>
fs.writeFile(filename, data, (err) => {
if (err !== null) {
resolve(E.left(err))
} else {
resolve(E.right(undefined))
}
})
),
log: (a) => fromIO(log(a)),
chain
}
// dependency injection
program5(DepsAsync)().then(console.log)Demo