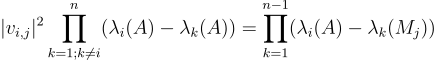This repository implements this paper that allows us to calculate eigenvectors from eigenvalues elegantly through PyTorch that allows your code to run on your CPU, GPU, or TPU.
Easily run it on your browser through Google Colab or copy the function locally.
Lemma 2. The norm squared of the elements of the eigenvectors are related to the eigenvalues and the submatrix eigenvalues.
Mathjax of Lemma 2
$$| v_{i, j} | ^ 2 \prod_{k=1; k \neq i}^{n} (\lambda_i (A) - \lambda_k (A)) = \prod_{k=1}^{n - 1} (\lambda_i (A) - \lambda_k (M_j))$$
Peter B. Denton, Stephen J. Parke, Terance Tao, and Xining Zhang
We present a new method of succinctly determining eigenvectors
from eigenvalues. Specifically, we relate the norm squared of the elements of
eigenvectors to the eigenvalues and the submatrix eigenvalues.
- PyTorch 1.9.1 (can be most versions of PyTorch as I used very core basic PyTorch functions)
- Python 3.8 (doesn't matter much as I use basic operations)
- If you would like to give some credit to this code implementation, these are the relevant links.
MIT