The Partially Observable Monte Carlo Planning (POMCP) online solver for POMDPs.jl.
Described in
Silver, D., & Veness, J. (2010). Monte-Carlo Planning in Large POMDPs. In Advances in neural information processing systems (pp. 2164–2172). Retrieved from http://discovery.ucl.ac.uk/1347369/
Problems should be specified using the POMDPs.jl interface. For more information, see the POMDPs.jl documentation.
This package replaces the deprecated POMCP.jl package. It has fewer features, but is much simpler.
In Julia 1.0 and higher, BasicPOMCP is available on the JuliaPOMDP registry (and this registry is required to automatically get the MCTS dependency):
using Pkg
Pkg.add("POMDPs")
using POMDPs
POMDPs.add_registry()
Pkg.add("BasicPOMCP")using POMDPs, POMDPModels, POMDPSimulators, BasicPOMCP
pomdp = TigerPOMDP()
solver = POMCPSolver()
planner = solve(solver, pomdp)
for (s, a, o) in stepthrough(pomdp, planner, "sao", max_steps=10)
println("State was $s,")
println("action $a was taken,")
println("and observation $o was received.\n")
endA minimal example showing how to implement a problem for the solver to use is here: https://github.com/JuliaPOMDP/BasicPOMCP.jl/blob/master/notebooks/Minimal_Example.ipynb
Solver options are set with keyword arguments to the BasicPOMCP constructor. The options are described in the docstring which can be accessed with ?POMCPSolver.
The output of ?POMCPSolver is printed below, but may not be up to date.
POMCPSolver(#=keyword arguments=#)Partially Observable Monte Carlo Planning Solver.
max_depth::IntRollouts and tree expension will stop when this depth is reached. default:20
c::Float64UCB exploration constant - specifies how much the solver should explore. default:1.0
tree_queries::IntNumber of iterations during each action() call. default:1000
estimate_value::AnyFunction, object, or number used to estimate the value at the leaf nodes. default:RolloutEstimator(RandomSolver(rng))
- If this is a function
f,f(pomdp, s, h::BeliefNode, steps)will be called to estimate the value.- If this is an object
o,estimate_value(o, pomdp, s, h::BeliefNode, steps)will be called.- If this is a number, the value will be set to that number Note: In many cases, the simplest way to estimate the value is to do a rollout on the fully observable MDP with a policy that is a function of the state. To do this, use
FORollout(policy).
default_action::AnyFunction, action, or Policy used to determine the action if POMCP fails with exceptionex. default:ExceptionRethrow()
- If this is a Function
f,f(pomdp, belief, ex)will be called.- If this is a Policy
p,action(p, belief)will be called.- If it is an object
a,default_action(a, pomdp, belief, ex)will be called, and if this method is not implemented,awill be returned directly.
rng::AbstractRNGRandom number generator. default:Base.GLOBAL_RNG
This solver does not reuse decision-making simulations for the belief update as in the original Silver and Veness paper. We have found that unweighted particle filtering approach to be unuseful in practice because
- The number of particles that comprise the next belief is small because only the particles in the branch corresponding to the actual action and observation can be used,
- Even in the Silver and Veness paper, domain-specific particle reinvigoration must be used, and
- The computation time required to run a standard weighted particle filter is small compared to the amount of time needed to plan with POMCP, so reusing the simulations gives minimal benefit.
Instead, a custom belief updater, or an updater from ParticleFilters.jl should be used.
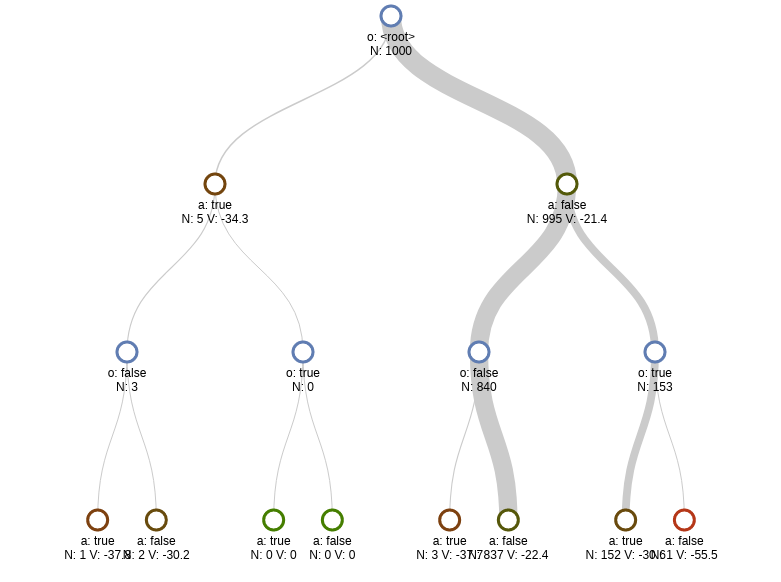
The search tree can be visualized with D3Trees.jl after running the action_info() as in the example below. Note: tree_in_info must be set to true either as a solver option or as a keyword argument to action_info() for this to work (it is disabled by default because it can use a lot of memory).
using POMDPs
using BasicPOMCP
using POMDPModels
using POMDPModelTools
using D3Trees
using Random
pomdp = BabyPOMDP()
solver = POMCPSolver(tree_queries=1000, c=10.0, rng=MersenneTwister(1))
planner = solve(solver, pomdp)
a, info = action_info(planner, initialstate_distribution(pomdp), tree_in_info=true)
inchrome(D3Tree(info[:tree], init_expand=3))This should produce the image at the top of the README.