handwritten-digit-classifier

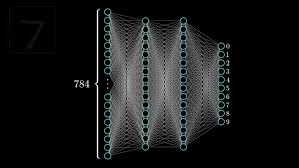
Deep Learning project using MNIST dataset. With this network max 88.6 +/- 0.2 percent was observed.

Neural Network Structure

Gradient descent to find global minima

Sigmoid function

Reduce any real number value in between 0 to 1.0

Introduction

Goal is to classify hand written digits. I've used [784-16-16-10] layer structure. One can play around with the net structure, keeping first and last layer fixed.

STRUCTURE

Dataset:
- Get training and test dataset from MNIST dataset.
- Each data is a (784x1) vector
- Each label is a (10x1) vector
- A total of 60000 training and 20000 test dataset
- Mini batch size is 16 i.e. each mini_batch contains 16 train dataset
Network:
- Initialize random weights and biases for all layers
- For each epoch
  - For each mini batch
    - For each data and label in mini batch
      - Activations calculation
      - Loss calculation
      - Delta values calculation with Gradient descent method
      - Nabla values calculation
      - Update weights and biases with learning rate 0.1
  - Evaluate network's accuracy for the test dataset

NB: Output layer consists total 10 neurons. Activation of each neuron denotes the corresponding digit.

Activation calculation

z = np.dot(w, a)+b
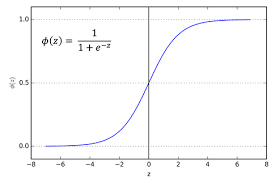
a = self.sigmoid(z)

Loss calculation

loss = np.sum(np.power(np.subtract(self.a[-1],y),2))/(2.0*self.dataset.mini_batch_size)

Cost derivative

cost_derivative = np.subtract(self.a[-1], y)

Derivative of activation

def sigmoid_derivative(a):
	return a*(1-a)


activation_derivative = sigmoid_derivative(activation)

Delta and nabla calculations

For output layer

delta = cost_derivative*self.sigmoid_derivative(self.a[-1])
self.nabla_w[-1] = np.dot(delta, self.a[-2].T)
self.nabla_b[-1] = delta

For hidden layers: codes for the previous layer of output

# For previous layer of the output-layer, L.
# delta in the right hand of the first eqn. is the output layer's delta
delta = np.dot(self.weights[L].transpose(), delta) * self.sigmoid_derivative(self.a[L-1])
self.nabla_b[L-1] = delta
self.nabla_w[L-1] = np.dot(delta, self.a[L-2].transpose())

weight = weight + (-learning_rate*mini_batch_size)*nabla_w
bias = bias + (-learning_rate*mini_batch_size)*nabla_b

Execute the codes

Install dependencies

pip3 install -r requirements.txt

Codes were written on Python v3.6.6

Run Network.py

python3 Network.py

rk4bir/digit-classifier