A finite differences simulation library.
This package lets you quickly build simple numerical simulations.
- Quickly build finite difference simulations with an arbitrary number of domains, scalars, dimensions and boundary conditions.
- Concise, clear syntax.
- Build models for CPU or GPU using Scipy or Cupy sparse libraries.
- Arbitrary derivative order and approximation accuracy.
- Partial model updates minimize overheads in iterative solutions.
- Implicit transient simulation.
pip install fastfd
# Import fastfd and select the scipy sparse library (or cupy for GPU support)
import fastfd as ffd
ffd.sparse_lib('scipy')
import numpy as np
# Define axes
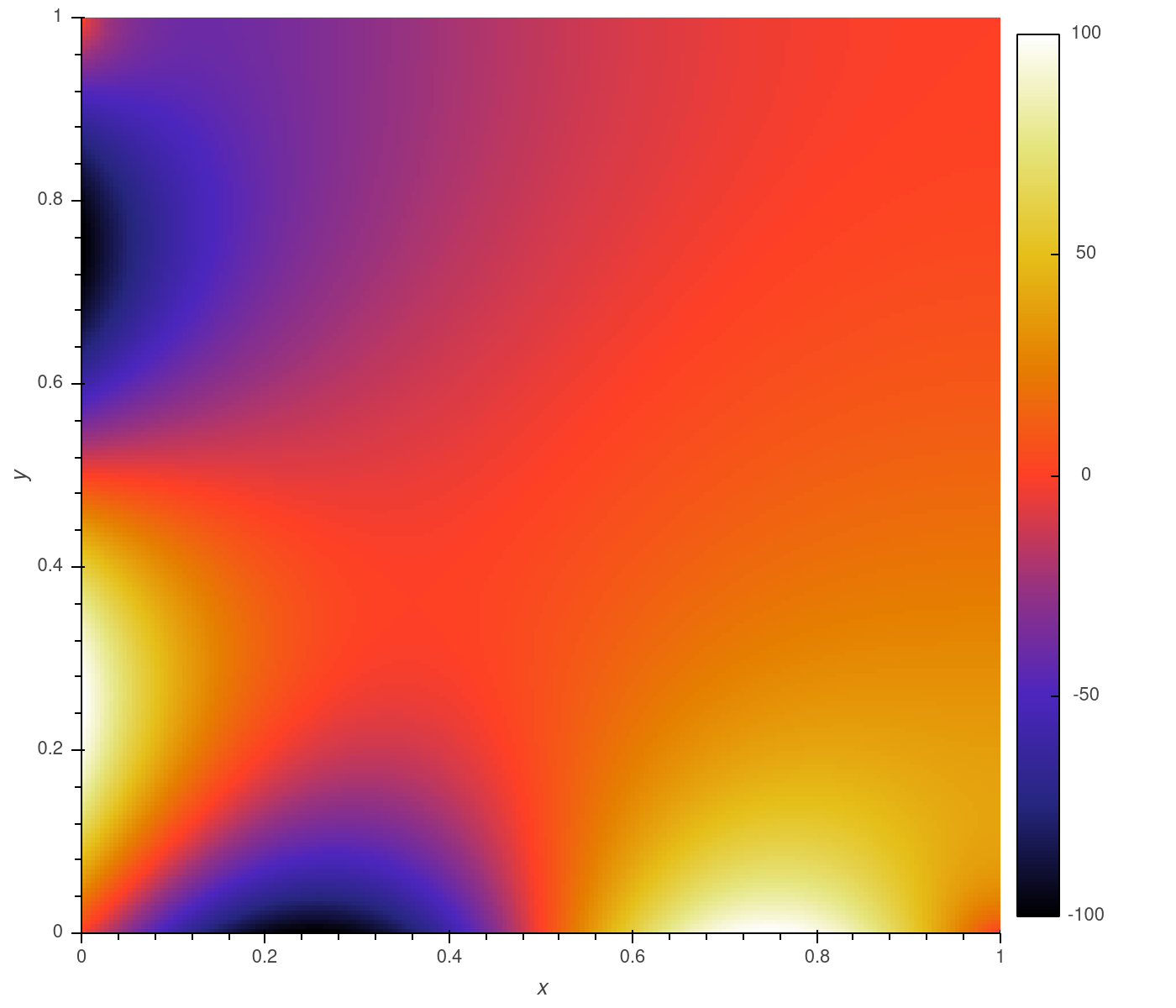
x = ffd.LinearAxis('x', start = 0, stop = 1, num = 201)
y = ffd.LinearAxis('y', start = 0, stop = 1, num = 201)
# Define scalars
T = ffd.Scalar('T', [x, y], accuracy = 4)
# Define the model
model = ffd.FDModel([T])
# Set model governing equations (thermal diffusion)
model.update_equations({
'Conductivity': ((T.d('x', 2) + T.d('y', 2)), 0),
})
# Set model boundary conditions
model.update_bocos({
'Tx=1 adiabatic': (T.i[-1, :], T.d('x')[-1, :], 0),
'Ty=1 adiabatic': (T.i[:, -1], T.d('y')[:, -1], 0),
'Tx=0 sinewave': (T.i[0, :], T.i[0, :], 100 * np.sin(x.coords * 2*np.pi)),
'Ty=0 sinewave': (T.i[:, 0], T.i[:, 0], -100 * np.sin(y.coords * 2*np.pi)),
})
# Solve the model
result = model.solve()FastFD can be set to use the Cupyx sparse libraries, though support is still a little rough around the edges. The current version of Cupy (8.5) only supports a least squares solver ('lsqr') which is much slower than the default 'spsolve'. However, spsolve will be implemented in the upcoming release of Cupy 9.0.
See example notebooks here: ./docs/examples for a more detailed explanation of how to use.