rmwkwok/forward_forward_algorithm

Implementation of Geoffrey Hinton's forward forward algorithm in tensorflow

Forward Forward algorithm in Tensorflow (Developing)

Paper: Geoffrey Hinton. The Forward-Forward Algorithm: Some Preliminary Investigations

Give up thinking it as a Model

I have rethought and concluded that building FF-based layers into a Model is not flexible enough for researching new ideas. Therefore, I gave up the concept of Model that I had adopted in my last implementation, and re-implemented this work which only has FFLayers (but no FFModel). A FFLayer (e.g. FFDense) class inherits the BaseFFLayer that contains a Tensorflow Layer (e.g. Dense).

The BaseFFLayer class

The BaseFFLayer enables a created FFLayer to perform 5 tasks:

1. TASK_TRANSFORM. Perform the tensorflow layer's transformation;
2. TASK_TRAIN_POS. Positive pass training;
3. TASK_TRAIN_NEG. Negative pass training;
4. TASK_EVAL. Evaluation;
5. TASK_EVAL_DUPED. Evaluation specialized for supervised-wise FF's goodness layer.

The TrainMgr class, and an example for unsuperwised-FF training

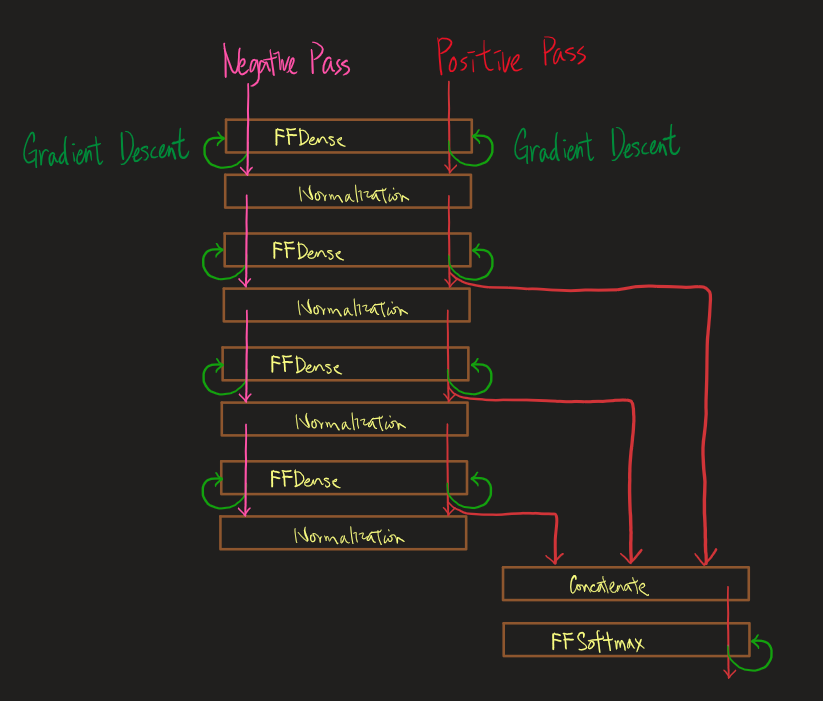
Since there is no Model, a TrainMgr is built to template the training loops and carry out metrics monitoring. It accepts a dict of layers and a training sequence function that connects the layers. For example, the following describes an unsupervised-wise FF based sequence:

layers = dict(
    # Utilities
    input = tf.keras.layers.InputLayer(name='input'),
    concat = tf.keras.layers.Concatenate(name='concat'),
    flatten = tf.keras.layers.Flatten(name='flatten'),
    preNorm = FFPreNorm(name='preNorm'),

    # FF layers
    b1 = FFDense(units=units, optimizer=Adam(0.0001), th_pos=.1, th_neg=.1, name=f'b1'),
    b2 = FFDense(units=units, optimizer=Adam(0.0001), th_pos=.1, th_neg=.1, name=f'b2'),
    b3 = FFDense(units=units, optimizer=Adam(0.0001), th_pos=.1, th_neg=.1, name=f'b3'),
    b4 = FFDense(units=units, optimizer=Adam(0.0001), th_pos=.1, th_neg=.1, name=f'b4'),

    # Classifiers
    softmax = FFSoftmax(units=NUM_CLASS, optimizer=Adam(0.001), name=f'softmax'),
)

def train_seq(X, y, y_ff):
    x = layers['input'](X)
    x = layers['flatten'](x)
    b1a = layers['b1'].ff_do_task(x, y_ff)
    b1n = layers['preNorm'](b1a)
    b2a = layers['b2'].ff_do_task(b1n, y_ff)
    b2n = layers['preNorm'](b2a)
    b3a = layers['b3'].ff_do_task(b2n, y_ff)
    b3n = layers['preNorm'](b3a)
    b4a = layers['b4'].ff_do_task(b3n, y_ff)
    b4n = layers['preNorm'](b4a)
    softmax_x = layers['concat']([b2n, b3n, b4n])
    y_pred = layers['softmax'].ff_do_task(softmax_x, y)

Pictorically:

How FF training works

In each epoch, for unsupervised-FF training, 3 datasets pass through the sequence.

1. First comes the positive data. After an positive mini-batch passes through the first FFDense, a gradient descent is done to update that FFDense. The transformed mini-batch then passes through the next FFDense, and another gradient descent is done to update the second FFDense, and the same sequence of operations are done for the other FFDense's and the FFSoftmax.
2. Then comes the negative pass which goes through only all the FFDense layers and performs gradient descent on them.
3. Last comes an evaluation dataset of only positive data.

The 3 datasets each requires the layers to perform a different set of tasks (among the 5 listed above). Therefore, 3 different tensorflow graphs can be built based on a train_seq python function as demonstrated above. To avoid graph retracing, the TrainMgr is responsible for storing built Graphs so that they can be reused from epoch to epoch.

Unsupervised-wise FF vs. Supervised-wise FF

My understanding is that an unsupervised-wise-FF-trained layer does not use any label information, whereas an supervised-wise-FF-trained layer uses it. Although the softmax that is appended as the last step of the unsupervised-wise FF algorithm uses the labels, it is not trained FF-wise, so the algorithm is still counted as unsupervised-wise-FF-trained.

Supervised-wise FF flow chart

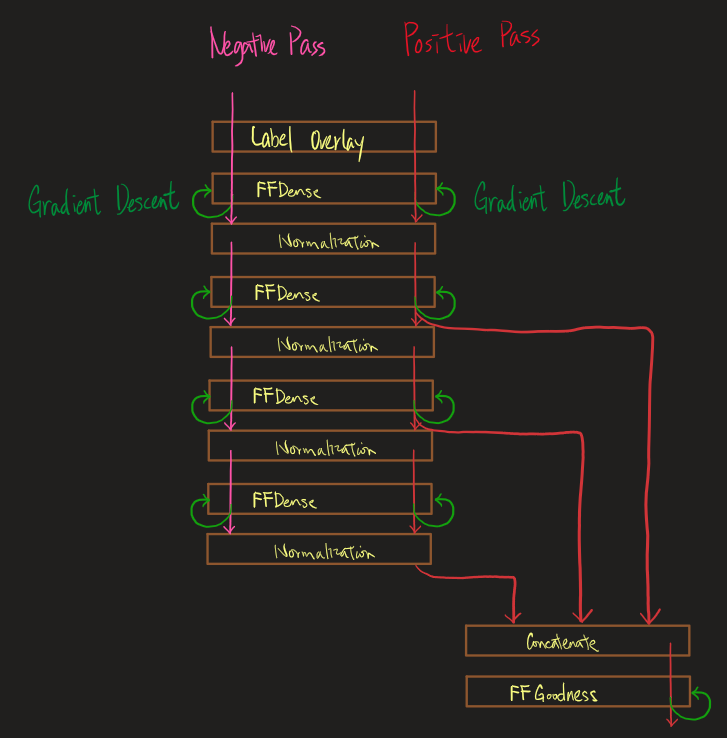An extra FFOverlay layer is added to the top of the sequence which will overlays on the sample its one-hot encoded label. At evaluation (TASK_EVAL_DUPED), the FFOverlay will replicate a sample to 5 copies which will each have one of the 5 one-hot encoded labels.

An FFGoodness replaces the FFSoftmax to receive some FFDense's outputs for computing goodness score.

The goodness formula

Although this formula was used by the paper as an example for positive data, I used the same also for negative data.

Result 2 (Updated on 26 Feb 2023)

The data

This time, all digits were used as positive data, instead of just five of them in Result 1. However, unlike the paper (again), I didn't use hybrid digits as negative data for unsupervised-wise FF. Instead, I split the digits into two sets (A & B), and divide a layer into two halves. The first half took set A as positive data and set B sa negative, whereas the second half did the opposite. Three digit splitting were explored, including (for both supervised and unsupervised-wise FF) "random splitting", "same splitting", and (only for supervised-wise FF) "no splitting".

Benchmark and summary

1. unsupervised-wise FF:

   • 97.1% @ units = 2000 and Random splitting

2. supervised-wise FF:

   • 94.7% @ units = 2000 and Random splitting
   • 95.1% @ units = 2000 and No splitting

(No hyperparameter tuning were done)

For more explanations and discussions, refer to this article.

Result 1 (Updated on 14 Feb 2023)

The data

Unlike the paper, I used digits 0, 1, 2, 3, and 4 from the MNIST dataset as the positive-pass's data, and the rest of the digits as the negative-pass's. At training, both positive and negative pass data are used. At evaluation, only a separate set of positive-pass data is done.

Benchmark and summary

The basic supervised and unsupervised results use the following settings:

1. units = 100 (number of units in each hidden layer)
2. batch_size = 128
3. data shuffling enabled
4. train all layers in every epoch
5. epochs = 200

Their validation accuracies are:

1. unsupervised-wise FF:
   • 96.64% @ basic setting
   • 98.44% @ changing to units = 500 and batch_size = 512
   • 99.06% @ changing to units = 2000 and batch_size = 512
2. supervised-wise FF:
   • 76.41% @ basic setting
   • 95.76% @ changing to units = 500 and batch_size = 512
   • 97.42% @ changing to units = 2000 and batch_size = 512

A similar setting with backprop can reach over 99% easily within 20 epochs.

For other results, observations, validation curves, and the layers' details, refer to examples/five_digits_as_positive/main.ipynb.