QCLIB: Quantum Computing library for Python
qclib is a simple Python library which allows to run quantum computing simulations[3,5,6] on an ordinary computer (the library provides a kind of virtual quantum computer). The computational complexity of such simulations run on a traditional computer obviously grows exponentially, and they can be used mainly for educational and demonstrative purposes in tasks small and trivial in size.
The main library code is qclib.py, there are also several example programs included using this library and allowing you to simulate several simple quantum algorithms in the quantum logic gate model (the Grover's search algorithm, superdense coding, quantum teleportation protocol).
The library was initially written in Python ver 2, but perhaps I will migrated it to Python 3 shortly in an experimental branch.
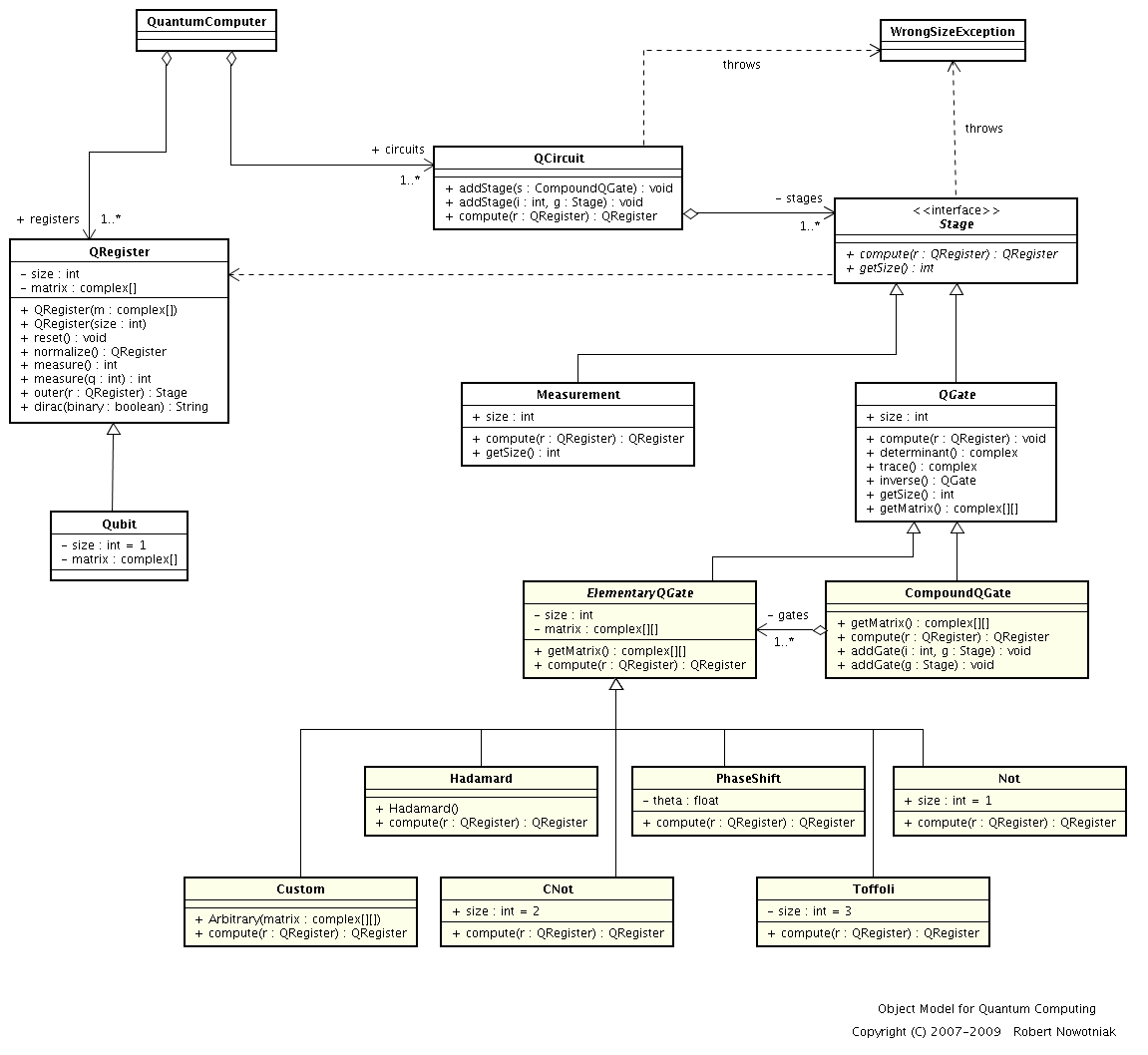
In order to enable quantum computer simulation I proposed the following object model, which was then implemented in Python in the qclib library.
The suggested model is inspired by an abstract syntax tree structure - and analogously - it makes it possible to express any computation in the quantum logic gate model using overloaded operators in Python.
The basic classes of the model are QRegister, representing a quantum register, and an abstract class QuantumGate, representing any given quantum gate. Concrete classes inherit from QuantumGate and overwrite the definition of the compute method. They are the elementary logic gates, like the Hadamard gate, Controlled-NOT gate, or phase shift gate.
The qclib library uses overloaded operators to wrap operations on unitary matrices which allows to express any quantum circuits. The operator ** hides the tensor product operation, while the overloaded operator * hides the composition mapping function, which corresponds to serial gate connection in a quantum circuit. Moreover, the overloaded operator () makes it possible to “call” the gates or quantum circuits and execute them in a way similar to quantum functions. The proposed object model is a very handy data structure for genetic algorithms processing and genetic programming (a type of genetic algorithms processing trees or graph structures).
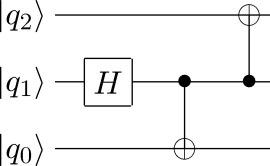
A very simple quantum circuit example and its implementation in qclib:
from qclib import *
circuit = (I ** Hadamard() ** I) * (I ** CNot()) * (CNot(0, 1) ** I)
result = circuit(ket0 ** ket0 ** ket0)
print result.dirac()
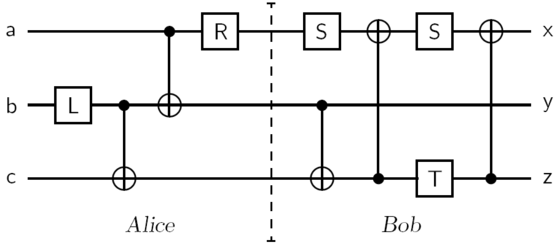
print result# quantum gates for Brassard teleportation circuit
L = Arbitrary(s2 * array([
[ 1, -1],
[ 1, 1],
]))
R = Arbitrary(s2 * array([
[ 1, 1],
[-1, 1],
]))
S = Arbitrary([
[ 1j, 0],
[ 0, 1],
])
T = Arbitrary([
[-1, 0],
[ 0, -1j],
])
psi = Qubit([
[ 2.0/7 * (cos(pi/2/9) + 1.0j*sin(pi/2/9)) ],
[ sqrt(45)/7 * (cos(pi/3*2) + 1.0j*sin(pi/3*2)) ],
])
alice = (I ** L ** I) * (I ** cnot) * (cnot ** I) * (R ** I ** I)
bob = (S ** cnot) * (I ** Swap()) * (cnot2 ** I) * \
(I ** Swap()) * (S ** I ** T) * (I ** Swap()) * (cnot2 ** I) * (I ** Swap())
input = psi ** ket0 ** ket0
qreg = alice(input)
cbits = qreg.measure(1, 2)
output = bob(qreg)
print cbits ** psi # expected cirtuit output
print output # teleporation circuit outputqregiter = epr()
b1 = 1
b2 = 0
# Perform coding operations on Alice qubit
if b1:
print (PhaseShift(pi) ** I)
qregiter = (PhaseShift(pi) ** I)(qregiter)
if b2:
qregiter = (Not() ** I)(qregiter)
B = Arbitrary([
[s2, 0, 0, s2],
[ 0, s2, s2, 0],
[s2, 0, 0, -s2],
[ 0, -s2, s2 , 0],
])
print B(qregiter).dirac()Please check in grover.py for the full Grover's algorithm implementation in qclib.
- C. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A. Peres, and W. Wootters. Teleporting an unknown quantum state via dual classical and EPR channels. Phys Rev Lett, pages 1895-1899, 1993.
- Lov K. Grover. A fast quantum mechanical algorithm for database search. In STOC ’96: Proceedings of the twenty-eighth annual ACM symposium on Theory of computing, pages 212-219, New York, NY, USA, 1996. ACM Press.
- Michael A. Nielsen and Isaac L. Chuang. Quantum Computation and Quantum Information. Cambridge University Press, 2000.
- A. Einstein, B. Podolsky, and N. Rosen. Can quantummechanical description of physical reality be considered complete? Phys. Rev., 47(10):777–780, May 1935.
- http://robert.nowotniak.com/en/quantum-computing/
- Nowotniak, Robert. On the evolutionary design of quantum algorithms (in Polish). 2008, Master’s thesis, Lodz University of Technology, 2008.
- Nowotniak, Robert. Analysis of quantum-inspired evolutionary algorithms (in Polish). 2015, Doctoral dissertation, Lodz University of Technology