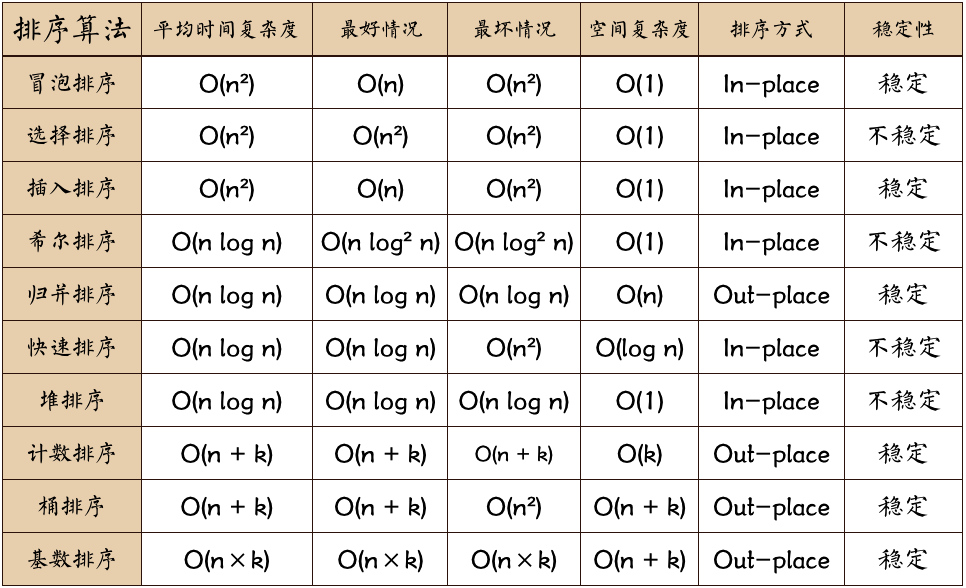
总结参考下图:
参考:博客
(1)特征工程指的是把原始数据转变为模型训练数据的过程,目的是过得更好的训练数据特征,使得机器学习模型逼近这个上限。包括:数据采集/清洗/采样,特征处理,特征构建,特征提取,特征选择。参考:博客1,博客2
(2)想到的两种方法:
- 使用非线性函数区分。
- 对数据进行非线性变换,将非线性问题变换为线性问题。如 SVM 中的 kernel method,将数据从现行不可分的输入空间映射到线性可分的特征空间。参考:统计学习方法 P116
映射函数为 phi(x): X -> H,则核函数为 K(x, z) = phi(x) phi(z)。
引入核函数可以解决非线性问题
常用的核函数:多项式核函数、高斯核函数。详见统计学习方法 P122
(1)根据 Loss 函数后加的正则项不同,分为 L1 正则和 L2 正则,L1 正则为权值的一范数(权值绝对值之和),L2 正则为权值的二范数平方(权值平方和)。参考:西瓜书P253
(2)两种解释:
- 数据计算:分别对加了正则项的 Loss 函数求导,则 L2 正则项在权值为 0 的时候导数为 0,而 L1 正则项在权值为 0 时的导数为正负 lambda,则引入 L2 正则对 Loss 函数在权值为 0 时的导数不产生影响,但是引入 L1 正则会使得 Loss 函数在权值为 0 时突变,若左右导数异号则说明此值为极小值,所以容易得到权值为 0。参考:博客
- 直观理解(几何空间):可观察二维平面内 Loss 函数与正则项的等值线,最优解为 Loss 函数与正则项之和最小的点,画图可知引入 L1 正则后,最优解在坐标轴上。参考:西瓜书 P253,博客
L1 正则由拉普拉斯先验导出,L2 正则由高斯先验导出。
(1)大致分为两类:
- 个体学习器间存在强依赖关系,必须串行生成的序列化方法。Boosting 为一个典型的代表:先使用初始训练集训练一个基学习器,然后根据其表现调整数据分布,使得先前基学习器做错的训练样本在后续受到更多的关注。其典型代表为 AdaBoost 以 Boosting 理解这个类别:后面的学习期依赖前面学习器的结果,所以不能并行训练,即必须串行训练。
- 个体学习器之间不存在强依赖关系,可同时生成的并行化方法。代表为 Bagging 和随机森林,Bagging:每次使用自助采样法采集样本,在不同的样本训练基学习器;随机森林:除了样本随机,又引入属性(特征)随机,即每个基学习器使用的样本和特征均不同。
(2)同第一问:是否存在强依赖?是否必须串行生成。
参考:西瓜书 P173
(1)GB(Gradient Boosting):在迭代的时候选择梯度下降的方向来保证最后的结果最好,模型的预测函数为所有基学习器的和,每次迭代中,基学习器的目标为拟合之前模型的 Loss 函数的负梯度(在使用平方误差损失函数的回归问题和使用指数损失函数的分类问题时,负梯度等价于预测值与真实值的差)。
(2)GBDT(Gradient Boosting Decision Tree):是 GB 中的一个特例,使用决策树作为基学习器,这里使用 CART 回归树,衡量最佳分割点时使用最小化平方误差(在分类问题中使用的是基尼指数)。
(3)XGBoost:
- 在目标函数上加了正则项,与叶节点数量和值有关。
- Loss 函数在梯度(一阶导)的基础上增加了二阶导,用二阶泰勒公式逼近。
- 对最佳分割点的衡量标准做了改变。
- 在很多地方做了加速,包括寻找最佳分割点的方法、数据缺失值的处理、特征处理的并行等。
(4)LGB(LightGBM):
-
树木生长算法,XGB 采用按层增长的方式,LGB 直接选择最大收益的节点(但是深度需要加以限制,否则容易过拟合)。
-
划分点搜索算法,XGB 采用对特征预排序的方法,LGB 采用直方图算法(将特征值分成许多小筒,在筒上搜索分裂点,减少计算和存储代价,获得更好的性能)。
-
其他:直方图做差优化,支持类别特征,支持并行运算
(5)RF(Random Forest):随机选取不同的特征和不同分布的数据训练基学习器,然后结合。
参考: 博客1,统计学习方法 P146 - P152,
(1)GBDT 和随机森林的相同点:
- 都是由多棵树组成
- 最终的结果都是由多棵树一起决定
(2)GBDT 和随机森林的不同点:
- 组成随机森林的树可以并行生成;而GBDT只能是串行生成
- 对于最终的输出结果而言,随机森林采用多数投票等;而GBDT则是将所有结果累加起来,或者加权累加起来
- 随机森林对异常值不敏感,GBDT对异常值非常敏感
- 随机森林对训练集一视同仁,GBDT是基于权值的弱分类器的集成
- 随机森林是通过减少模型方差提高性能,GBDT是通过减少模型偏差提高性能
参考:机器学习基础
### sigmoid 函数的导数和取值范围是多少
导数: $$ f(x)^{'} = f(x)(1 - f(x)) $$ 取值为(0, 0.25]
(1)概念:
- 最小二乘:使用欧氏距离的平方作为度量单位,目标为预测值与真实值的距离越接近越好(预测值与真实值之差的平方和最小)。
- 极大似然估计:从概率角度解释,等价于以 KL-divergence作为度量单位,目标为预测到真实值的概率越大越好,需要已知概率分布,一般假设正态分布。
(2)关系:在极大似然估计假设概率分布为正态分布时,两者是等价的,即预估计结果相同。
从概率统计的角度处理线性回归并在似然概率为高斯函数的假设下同最小二乘简历了联系
- 准确率:在预测的所有结果中,预测正确的占比。
- 查准率(精度):在预测为正类的结果中,预测正确的占比。
- 查全率(召回率):在真实为正类的结果中,预测正确的占比。
- F1 度量:精度和召回率的调和平均。
- PR 曲线:横坐标是召回率,纵坐标为精度。
- ROC 曲线(Receiver Operating Characteristic Curve):横坐标是负类召回率(在真实为负类的结果中,预测错误占比),纵坐标为召回率。
- AUC(area under curve): ROC 曲线下方的面积。
增加模型复杂度(加深加宽神经网络,SVM使用核函数等),构建新特征。
### L2 正则的本质
限制解空间范围,缩小解空间,控制模型复杂度。
信息增益(ID3)、信息增益比(C4.5)、基尼指数(CART分类树)、平方误差(CART回归树)
参考:统计学习方法 P60 - P68
树模型计算分裂点时会根据一个标准(如上一个问题所述),特征重要性就是这个标准减小量的归一化值。可以理解为这个特征使得原始预测值的不确定性减小的程度,或误差减小的程度。
参考:博客
(1)样本随机、特征随机。
(2)两种方法:
- 使用基尼指数计算特征重要性(同上个问题),然后多棵树计算平均。
- 对于某棵树,使用OOB(袋外)样本计算误差,接着对某个特征加噪声(生成随机值或随机排序)再使用 OOB 样本计算误差,则误差增加程度可以表示这个特诊的重要性,再对所有的树取均值来表示该特征的重要性。
- 回归:
(1)MSE(均方差),RMSE(均方根误差),MAE(平均绝对值误差),Huber 损失
(2)MSE 对于异常值较为敏感,受异常值影响较为严重,RMSE 和 MAE 对于异常值更稳定。但是 MAE 梯度不变,对于需要计算梯度模型不利,而 RMSE 计算较为麻烦。Huber 损失是 MSE 和 MAE 的结合,在绝对值损失小于阈值时变为平方损失,大于阈值时变为绝对值损失,保留了两者的优点。
- 分类:
(1)0-1损失函数(预测正确为0,预测错误为1),logistic 损失(对 logistic 回归函数求极大似然函数得到,等价与交叉熵,hinge loss(合页损失),指数损失,modified Huber loss。
(2)0-1 损失函数对错点惩罚相同,不合适。logistic 损失和合页损失在预测错误时惩罚以线性增长,但是 logistic 损失可以进行概率估计,合页损失在预测正确时可以产生稀疏解提高训练效率。modified Huber loss 结合了两者的优点。在 yf(x) < -1 时惩罚以线性增长受异常点干扰较少,在 yf(x) >1 时产生稀疏解。
参考:博客
(1)离散特征的增加和减少都很容易,易于模型的快速迭代。
(2)稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展。
(3)对异常数据具有较强的鲁棒性。
(4)单个特征离散化为 N 个后,每个特征有单独的权重,相当于引入了非线性,增加了模型的表达能力,加大了拟合能力。
(5)可以特征交叉,M + N 个特征变为 M * N 个特征,进一步引入非线性,提升表达能力。
参考:知乎
梯度下降使用所有的数据,随机梯度下降使用单个数据,若使用一批数据则为批量梯度下降。梯度下降计算准确的梯度,但是迭代速度慢,随机梯度下降估计梯度,不一定准确但是迭代速度快,批量梯度下降估计的梯度更准确且迭代速度较快,所以一般采用批量梯度下降。
因为牛顿法需要求解目标函数的 Hession Matrix 的逆矩阵,计算比较复杂。拟牛顿法使用一个正定矩阵来近似代替 Hession Matrix。
参考:统计学习方法 P219 - P222
推到思路:定义任意角度单位向量,计算方向导数,推到得到方向和梯度同向时方向导数最大。
参考:知乎
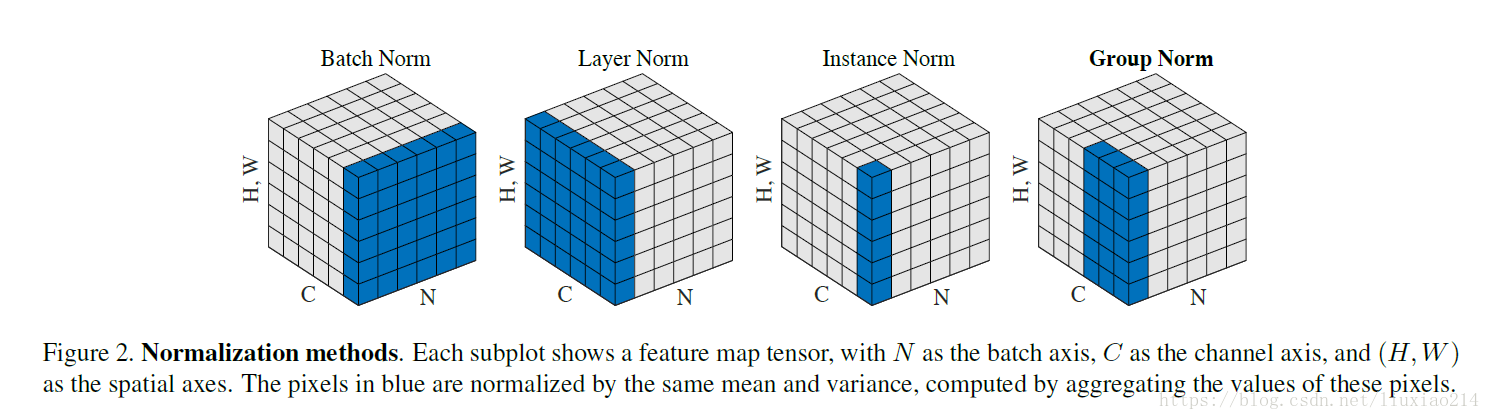
(1)BN 相当于把一个 batch 的一个 channel 的所有数据当做一组特征,将这组特征进行 normalization,特征组数和 channel 的个数相同,相当于均值方差的个数是和特征的组数相同。在训练的时候保存计算的均值和方差,在测试时使用。
BN 的缺点:
- 对 batch size 的大小比较敏感,如果 batch size 太小,计算的均值和方差不足以代表整个数据分布。
- 对固定长度的网络方便,但是对 RNN 这种长度不固定的网络计算很麻烦。
(2)LN 是针对每个样本的所有特征进行 normalization,得到的均值方差个数和 batch size 相同。具体参考下图,其中 H、W 为图像的高和宽,C为 channel,N 为 batch size。
参考:博客
### AlexNet,VGG,GoogleNet,Residual Net 各自的贡献是什么?
题目来源:博客