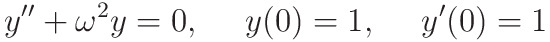The progress in quantum computing over the past few years has been notable, with increasing technology being developed for quantum computers annually. In this context, there are quantum computers with hundreds of qubits capable of running quantum algorithms with circuit depths of up to several thousand gates while still producing significant results. A primary challenge in this field is the creation of efficient and innovative quantum algorithms that provide exponential speedups over classical methods. One notable example of such an algorithm is "A Quantum Algorithm for Solving Linear Differential Equations: Theory and Experiment", presented by Tao Xin, et al. in 2020.
Like most quantum algorithms papers, this is theoretical work. Implementing a theoretical paper in practice is a massive challenge, with many obstacles that need to be overcome, both theoretically and implementation-wise.
Your challenge is to implement the above paper using the Classiq platform.
Classiq is an end-to-end quantum software platform that enables you to design, optimize, analyze and execute quantum algorithms. Classiq utilizes the power of high-level functional design and enables you to focus on the algorithm you want to create rather than on its quantum circuit implementation.
The goal is to apply the above algorithm to a simple differential equation. For this, you should
solve the harmonic oscillator equation, with frequency
After solving this equation using the algorithm, you should:
- Use the output as a means to evaluate the kinetic and potential energy of the system as
a function of time in the interval
$[0, 1]$ . - Analyze how the kinetic and potential energy values vary when you try different values
for the bounds in functions that require it (for example, the
inplace_prepare_state()). - Analyze the count gate when optimizing the circuit in width or depth.
- Final presentation that explains your solution and your implementation
- The jupyter notebook you worked with
- The .qmod files that capture your models (a detailed explanation of how to do this can be found in this notebook)
- The .qprog files that captures your quantum programs (a detailed explanation of how to do this can be found in this notebook)
- Fork this GitHub repository.
- After working on the challenge implementation, add all your submission files (as listed above) to your fork.
- Create a pull request on the original Q-SITE repository which includes your submission.
TODO: Tutorial video demonstrating above instructions coming soon.
If you are new to Classiq, we recommend starting with these guiding materials:
- Classiq 101 will give you a smooth start with the platform and a general understanding of its concepts.
- The one-hour-long Classiq Fundamentals Workshop covers the basics of Classiq, including some hands-on exercises to get you started.
- The walkthrough on the platform home page will give you a tour of the platform and its architecture.
Good luck!
(A PDF version of the same documentation in this README has been provided too.)