MFEM + PyMFEM (FEM library)

This repository provides Python binding for MFEM. MFEM is a high performance parallel finite element method (FEM) library (http://mfem.org/).

Installer (setup.py) builds both MFEM and binding together. By default, "pip install mfem" downloads and builds the serial version of MFEM and PyMFEM. Additionally, the installer supports building MFEM with specific options together with other external libraries, including MPI version.

Install

pip install mfem                    # binary install is available only on linux platforms (Py36-310)
pip install mfem --no-binary mfem   # install serial MFEM + wrapper from source

Build with additional features (MPI, GPU, GPU-Hypre, GSLIB, SuiteSparse, libCEED, LAPACK)

The setup script accept various options. TO use it, one can either use --install-option flag with pip, or download the package manually and run the script. For example, the one below downloads and build parallel version of MFEM library (linked with Metis and Hypre) and installs under /mfem. See also, docs/install.txt

Using pip

$ pip install mfem --install-option="--with-parallel"

Build from local source file

# Download source and build
$ pip download mfem --no-binary mfem (expand tar.gz file and move to the downloaded directory)
or clone this repository
$ git clone https://github.com/mfem/PyMFEM.git

# Then, build it from local source
$ python -m pip install ./ --install-option="--with-parallel" --install-option="--mfem-branch=master"
or
$ python setup.py install --with-parallel # it download and build metis/hypre/mfem

# Verbose output
$ python setup.py install --verbose # SWIG output and CMAKE_VERBOSE_MAKEFILE is on

# Cleaning
$ python setup.py clean --all # clean external dependencies + wrapper code

# Choosing compiler
$ python setup.py install --with-parallel --CC=icc --CXX=icpc --MPICC=mpiicc --MPICXX=mpiicpc

# Run test
cd test
python test_examples.py -serial

# For other configurations, see docs/install.txt or help
$ python setup.py install --help

Usage

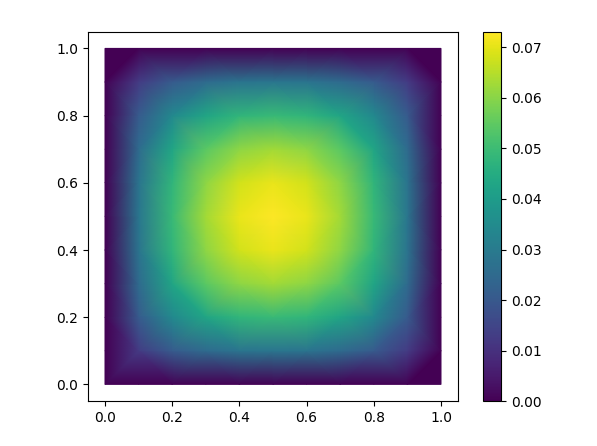
Here is an example to solve div(alpha grad(u)) = f in a square and to plot the result with matplotlib (modified from ex1.cpp). Use the badge above to open this in Binder.

import mfem.ser as mfem

# create sample mesh for square shape
mesh = mfem.Mesh(10, 10, "TRIANGLE")

# create finite element function space
fec = mfem.H1_FECollection(1, mesh.Dimension())   # H1 order=1
fespace = mfem.FiniteElementSpace(mesh, fec)

#
ess_tdof_list = mfem.intArray()
ess_bdr = mfem.intArray([1]*mesh.bdr_attributes.Size())
fespace.GetEssentialTrueDofs(ess_bdr, ess_tdof_list)

# constant coefficient (diffusion coefficient and RHS)
alpha = mfem.ConstantCoefficient(1.0)
rhs = mfem.ConstantCoefficient(1.0)

# Note:
#    Diffusion coefficient can be variable. To use numba-JIT compiled
#    functio. Use the following, where x is numpy-like array.
# @mfem.jit.scalar
# def alpha(x):
#     return x+1.0
#

# define Bilinear and Linear operator
a = mfem.BilinearForm(fespace)
a.AddDomainIntegrator(mfem.DiffusionIntegrator(alpha))
a.Assemble()
b = mfem.LinearForm(fespace)
b.AddDomainIntegrator(mfem.DomainLFIntegrator(rhs))
b.Assemble()

# create gridfunction, which is where the solution vector is stored
x = mfem.GridFunction(fespace);
x.Assign(0.0)

# form linear equation (AX=B)
A = mfem.OperatorPtr()
B = mfem.Vector()
X = mfem.Vector()
a.FormLinearSystem(ess_tdof_list, x, b, A, X, B);
print("Size of linear system: " + str(A.Height()))

# solve it using PCG solver and store the solution to x
AA = mfem.OperatorHandle2SparseMatrix(A)
M = mfem.GSSmoother(AA)
mfem.PCG(AA, M, B, X, 1, 200, 1e-12, 0.0)
a.RecoverFEMSolution(X, b, x)

# extract vertices and solution as numpy array
verts = mesh.GetVertexArray()
sol = x.GetDataArray()

# plot solution using Matplotlib

import matplotlib.pyplot as plt
import matplotlib.tri as tri

triang = tri.Triangulation(verts[:,0], verts[:,1])

fig1, ax1 = plt.subplots()
ax1.set_aspect('equal')
tpc = ax1.tripcolor(triang, sol, shading='gouraud')
fig1.colorbar(tpc)
plt.show()

License

PyMFEM is licensed under BSD-3. Please refer the developers' web sites for the external libraries