torch-harmonics is a differentiable implementation of the Spherical Harmonic transform in PyTorch. It was originally implemented to enable Spherical Fourier Neural Operators (SFNO). It uses quadrature rules to compute the projection onto the associated Legendre polynomials and FFTs for the projection onto the harmonic basis. This algorithm tends to outperform others with better asymptotic scaling for most practical purposes.
torch-harmonics uses PyTorch primitives to implement these operations, making it fully differentiable. Moreover, the quadrature can be distributed onto multiple ranks making it spatially distributed.
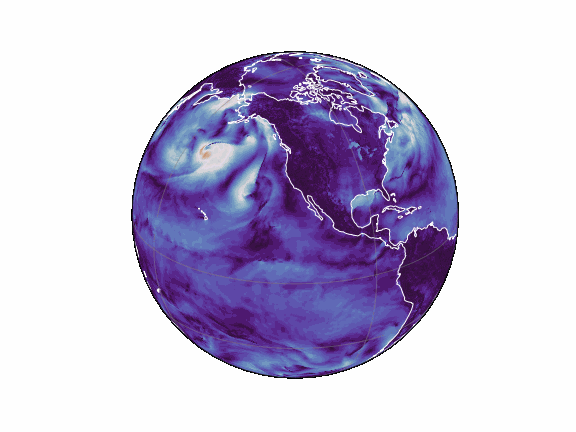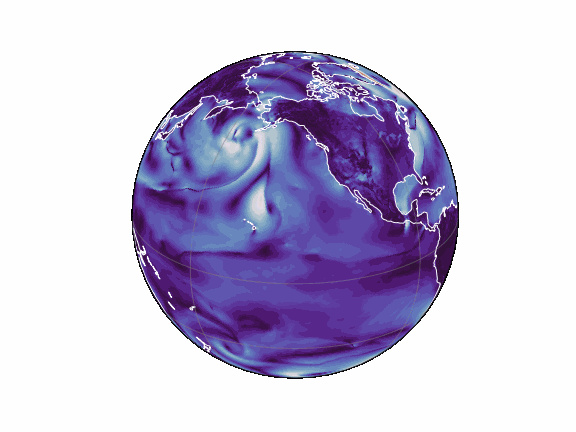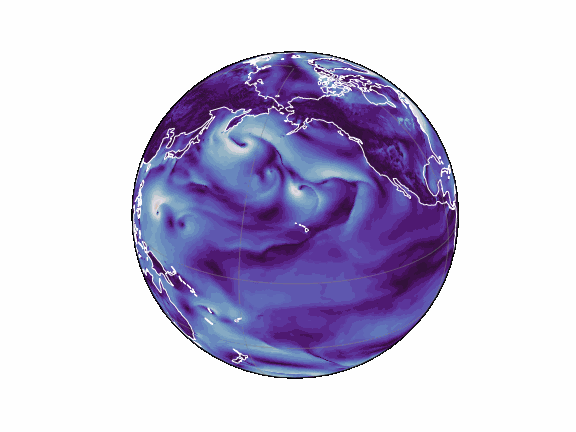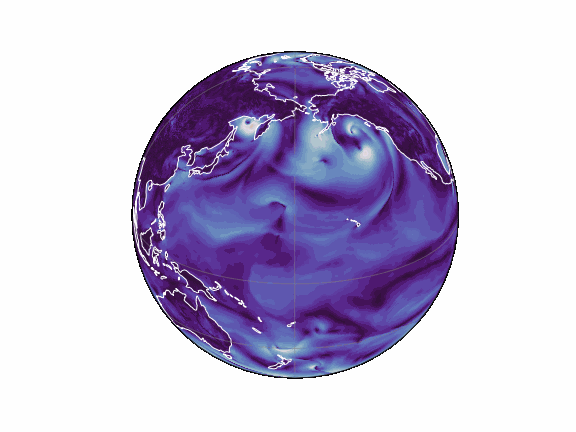
torch-harmonics has been used to implement a variety of differentiable PDE solvers which generated the animations below. Moreover, it has enabled the development of Spherical Fourier Neural Operators (SFNOs) [1].
 |
 |
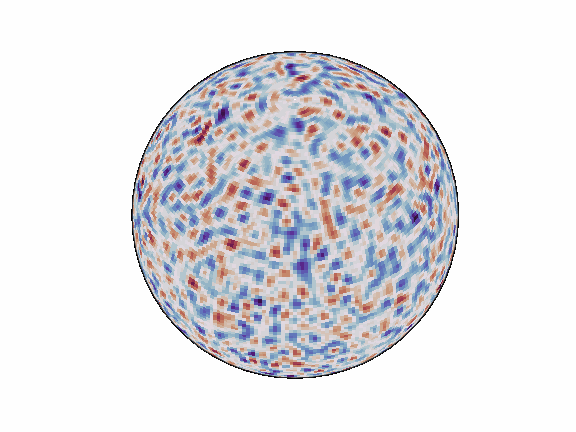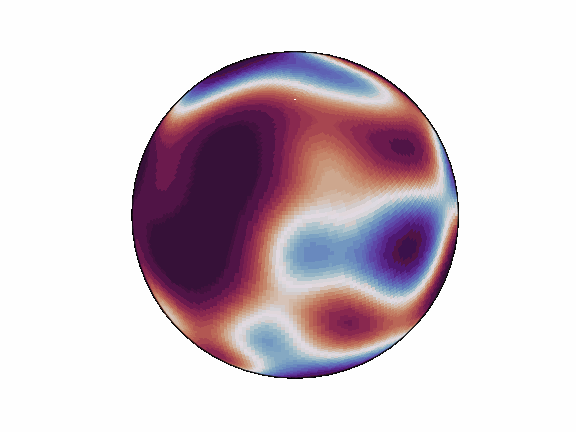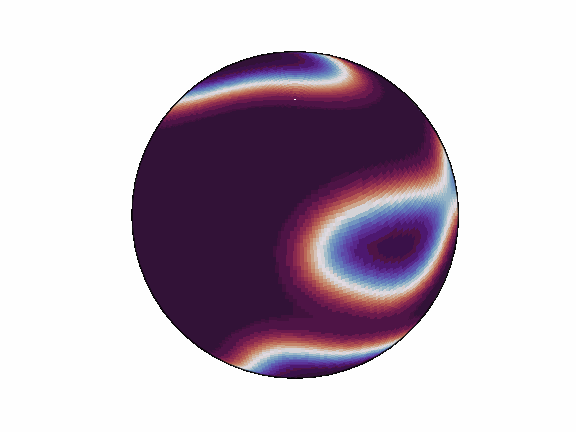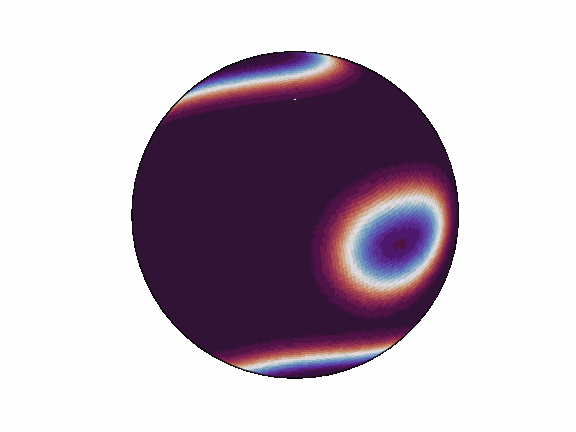 |
Download directyly from PyPI:
pip install torch-harmonics
Build in your environment using the Python package:
git clone git@github.com:NVIDIA/torch-harmonics.git
cd torch-harmonics
pip install -e .
Alternatively, use the Dockerfile to build your custom container after cloning:
git clone git@github.com:NVIDIA/torch-harmonics.git
cd torch-harmonics
docker build . -t torch_harmonics
docker run --gpus all -it --rm --ipc=host --ulimit memlock=-1 --ulimit stack=67108864 torch_harmonics
- Boris Bonev (bbonev@nvidia.com)
- Thorsten Kurth (tkurth@nvidia.com)
- Christian Hundt (chundt@nvidia.com)
- Nikola Kovachki (nkovachki@nvidia.com)
- Jean Kossaifi (jkossaifi@nvidia.com)
The implementation follows the algorithm as presented in [2].
The truncated series expansion of a function
where
A direct spherical harmonic transform can be accomplished by a Fourier transform
in longitude and a Legendre transform
in latitude.
in order to apply the Legendre transfor, we shall use Gauss-Legendre points in the latitudinal direction. The integral
is approximated by the sum
The main functionality of torch_harmonics is provided in the form of torch.nn.Modules for composability. A minimum example is given by:
import torch
import torch_harmonics as th
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
nlat = 512
nlon = 2*nlat
batch_size = 32
signal = torch.randn(batch_size, nlat, nlon)
# transform data on an equiangular grid
sht = th.RealSHT(nlat, nlon, grid="equiangular").to(device)
coeffs = sht(signal)To enable scalable model-parallelism, torch-harmonics implements a distributed variant of the SHT located in torch_harmonics.distributed.
If you use torch-harmonics in an academic paper, please cite [1]
@misc{bonev2023spherical,
title={Spherical Fourier Neural Operators: Learning Stable Dynamics on the Sphere},
author={Boris Bonev and Thorsten Kurth and Christian Hundt and Jaideep Pathak and Maximilian Baust and Karthik Kashinath and Anima Anandkumar},
year={2023},
eprint={2306.03838},
archivePrefix={arXiv},
primaryClass={cs.LG}
}
[1] Bonev B., Kurth T., Hundt C., Pathak, J., Baust M., Kashinath K., Anandkumar A.; Spherical Fourier Neural Operators: Learning Stable Dynamics on the Sphere; arXiv 2306.0383, 2023.
[2] Schaeffer N.; Efficient spherical harmonic transforms aimed at pseudospectral numerical simulations; G3: Geochemistry, Geophysics, Geosystems, 2013.
[3] Wang B., Wang L., Xie Z.; Accurate calculation of spherical and vector spherical harmonic expansions via spectral element grids; Adv Comput Math, 2018.

