Chess Position Ranking

The following 3 positions have two things in common.

white to move	black to move	black to move

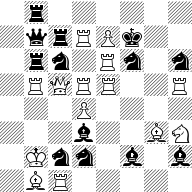They're all legal. That is, reachable from the starting position in a valid game of chess.
They're randomly generated.
In fact, these 3 are all the legal positions among a sample generated by picking 100 random integers in a specific range, and converting each integer into a corresponding position. Hovering over each position will show the integer used to generate it.

Rankings

The conversion from integers to positions is made possible by a so-called ranking, which is a triple consisting of a size, an unrank function that maps integers in the range 0..size-1 to objects, and a rank function that maps objects to integers. A ranking is invertible when the rank and unrank functions form a bijection, giving each object a unique rank.

The objects in our chess ranking are actually not mere positions, but positions annotated with some additional data generated during the unranking process. For simplicity, we call them uniquely rankable positions, or urpositions for short. Each chess position can occur as multiple equivalent urpositions, giving it an associated multiplicity.

This Haskell based software suite implements an invertible ranking of N = 8726713169886222032347729969256422370854716254 (~ 8.7E45) urpositions. The main executable, cpr, uses Forsyth–Edwards Notation for input and output of urpositions, with the following modifications:

the en-passant field is only used with an opponent pawn present to capture
the last two fields record multiplicity and the rank of the urposition in a ranking of equivalent ones.

Estimating the number of legal positions

The 3 legal positions all have a multiplicity of 1, while the average 1/multiplicity of all 100 positions is ~ 0.9833. With a 95% confidence level, this yields an estimated number of legal positions of (3% +- 1.96 * sqrt(3% * 97% / 100)) * N / 1, or (2.6+-2.9)x10^44, which is far less than one digit of accuracy, and barely gives us the order of magnitude.

To obtain a full digit of accuracy, we need to reduce the error by about a factor of 10, which requires a 100x bigger sample. File "testRnd10kResearch" contains a sample of 10,000 random positions subjected to a relatively simple legality check, that finds all but 923 positions to be illegal for trivial reasons. Under milestone "10k", I have filed a separate issue for each of the 923 potentially legal positions in the 10k sample.

Mario Richter kindly contributed the output of his legality checking program "rawbats", which found 132 of the 923 positions to be illegal. Altogether, 538 are proven legal with a proof game constructed for each, and 385 determined to be illegal with an illegality proof sketch. The 538 legal positions have an average 1/multiplicity of ~ 0.97847, somewhat lower than the ~ 0.98467 average of all 10000.

This yields an estimated number of legal positions of (5.38% +- 1.96 * sqrt(5.38% * 94.62% / 10000)) * N * 0.97847, or (4.59 +- 0.38) * 10^44, again with 95% confidence level.

More recently, Peter Österlund used his Texel chess engine to test all 923 positions for legality. Texel found that all 385 positions determined illegal by manual analysis, lack a proof game kernel, which is a necessary condition for legality. For the other 538 positions with proof games, it did find corresponding proof kernels. Thus, Texel's analysis (reproduced in file Texel.923) fully corroborates the manual analysis.

Reproducibility

We generated legal FENs by playing chess games with moves chosen uniformly at random among all legal ones, and 1% chance of termination after every move. We sorted and ranked all these FENs and unranked the results to verify invertibility of ranking (Makefile targets testRnd100kLegalFENs and testRnd1mLegalFENs). In order to be able to sort FENs, we added a fourth component to our former Ranking triple, namely a function to compare two ranked elements.

We produced our integer samples using Haskell's built-in random number generator with a seed of 0, and sorted the result for use in batched ranking (Makefile targets testRnd100Ranks, testRnd1kRanks, testRnd10kRanks, and testRnd100kRank). NOTE: random-1.1 was used for our results. The newer random-1.2 produces different results.

We unranked these to obtain random urpositions (Makefile targets testRnd100FENs,testRnd1kFENs, testRnd10kFENs, and testRnd100kFENs). NOTE that these can take over half an hour to complete.

We checked invertibility by ranking the results (Makefile targets testRnd100Ranking, testRnd1kRanking, testRnd10kRanking, and testRnd100kRanking), and comparing with the original integers used for unranking.

We ran some legality tests that find ~95% of the positions to be definitely illegal (Makefile targets testRnd100Research, testRnd1kResearch, testRnd10kResearch, testRnd100kResearch).

The file sortedRnd1kResearchManual extends sortedRnd1kResearch with a manual determination of legality of the 93 remaining positions in the 1k sample.

Related Work

Estimates of the number of legal chess positions date back to Claude Shannon's seminal 1950 paper.

The reason for satisfying ourselves with a mere estimate is that we have no hope of ever determining the number exactly, like we did in the game of Go. Whereas in Go, deciding whether a given position is legal is quite simple, determining the legality of a given chess position is exceedingly hard. It is the essence of so-called retrograde analysis problems that concern the possible past moves rather than the possible future moves that normal chess problems concern themselves with.

The reader is invited to study some of the best retrograde problems ever composed, together with their intricate solution, at this ``Masterworks'' collection. Evidence of the algorithmic hardness of retrograde problems may be found in this recent computational complexity paper that proves retrograde decision problems on arbitrarily large chess boards to be PSPACE-hard.

In his 1994 PhD thesis, Victor Allis claims a calculated upper bound of 5E52 and assumed "the true state-space complexity to be close to 1E50". We suspect a programming bug led to these numbers being many orders of magnitude too large.

In 1996, Shirish Chinchalkar obtained an upper bound of 1.77894E46. A copy of the program that Shirish Chinchalkar developed to compute his upperbound may be found in Will Entriken's github repo, which also contains his software for ranking chess diagrams.

In 2014, Stefan Steinerberger derived an upper bound of approximately 1.53x10^40 on the number of diagrams with no promoted pawns. We improve this down to 2891398339895958031893456691621753206624 ~ 2.9x10^39 by constraining the number of unopposed pawns according to pawns and pieces captured (Makefile target noproms).

Bug Bounties

Since validity of these results hinges on the ranking including all legal positions, a bounty of $256 is hereby offered to the first person to file an issue with a legal but unrankable position. A bounty of $128 is offered for a rankable position for which unranking reports the wrong multiplicity. Finally, a bounty of $64 is offered for a proof game for one of the 385 positions claimed to be illegal, or one of the 9077 position judged illegal by src/Lagality.hs

Interesting observations

The upper bound of N = 8726713169886222032347729969256422370854716254 is computed in under 10s by CountChess.hs (Makefile target count).

The original ranking implementation based on Data/Ranking.hs took on the order of 10s per position on top of the startup time of around 30 mins. Adding the batched rankings of Data/Ranking/Batched.hs resulted in huge speedups where many millions of positions could be generated within an hour.

The entire urposition ranking is composed out of 14 separate functions called

sideToMoveRanking
caseRanking
wArmyStatRanking bArmyStatRanking
guardRanking
enPassantRanking epOppRanking sandwichRanking
opposeRanking pawnRanking castleRanking wArmyRanking bArmyRanking pieceRanking

The input to each function is some data representing earlier choices, while the output is a ranking of further choices. Functions on the same row compose like a cartesian product, i.e. making choices independent of each other. The efficiency of the entire ranking is mostly attributable to the large final row.

The maximum multiplicity of 2 * 70 = 140 is achieved on positions where 4 pieces but no pawns were captured (courtesy of opposeRanking), and with an en-passant pawn landing between two opponent pawns (courtesy of enPassantRanking). For example, unranking 4363356584943110212154534698526026458664867108 yields FEN output "r3kb1r/ppp1pp1p/3p4/5PpP/8/8/PPPPP1P1/RNBQKBNR w KQkq g6 99 140".

Treating placement of kings just like that of other pieces hugely simplifies the ranking, but allows positions with adjacent kings. Avoiding adjacent kings only improves the upper bound by 10%, which is not worth the complications and resulting slowdowns,

Most urpositions (72.5%) have 4 captures, which supports up to 12 promotions. The next most common capture counts are 5 (20%), 3 (5.7%), 6 (1.9%) and 7 (0.1%).

The number of promotions is much more evenly distributed, with 4 through 12 promotions accounting for 0.3%, 1.1%, 3.4%, 8.3%, 15.2%, 21.5%, 22.7%, 17.1%, 8.3%, and 2% of random urpositions.

The 1 million sample classifies as

$ src/legal < sortedRnd1mFENs | grep "^ " | sort | uniq -c | sort -rn
492045  Illegal Both Kings in Check
173401  Illegal Side not to move in Check
102541  Illegal Adjacent Kings
79019  Illegal Bishops Too Monochromatic
53063  Single Check
35584  No Checks
29962  Illegal Triple Check
27541  Illegal Double Check
6130  Discovered Double Check
 714  Illegal Double Knight Check

leaving 53063 + 35584 + 5839 = 94486 positions for manual analysis.

Some people might enjoy minimizing the number of moves in a Proof Game, in what could be a friendly "Chess golf" competition, similar to Code golf.

Future work

More accuracy can be obtained by analysing the 100x larger sample testRnd1mResearch, giving 2 digits of accuracy at the 95% confidence level. Analyzing such a large sample will require additional software to aid both in proof game construction and in much more comprehensive detection of illegality, in order to keep the necessary manual analysis within manageable limits.

Recent advancements in the Texel chess engine by Peter Österlund bring us close to that goal. Of the 94903 possibly legal positions in testRnd1mResearch, it finds 38866 lack a proof kernel and should thus be illegal. For the other 56037 positions, it finds a proof kernel, but not necessarily a proof game.

With Peter's plans to improve Texel's ability to synthesize proof games from proof kernels, we can look forward to better estimates in the future.

The Future is here

Further advancements in Texel, applied to the 1M sample, have now proved 943977 positions illegal and 55958 positions legal. Of the remaining 1000000-943977-55958 = 65 positions, 53 were manually proven legal, and 12 were manually proven illegal, giving an exact total of 56011 legal positions, with an average 1/multiplicity of ~ 0.98013 (versus ~ 0.98583 for all 1M).

This yields an estimated number of legal positions of (5.6% +- 1.96 * sqrt(5.6% * 94.4% / 10000)) * N * 0.98013, or (4.79 +- 0.04) * 10^44, again with 95% confidence level.