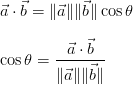The cosine similarity between two vectors is a measure that calculates the cosine of the angle between them. This metric is a measurement of orientation and not magnitude, it can be seen as a comparison between documents on a normalized space because we’re not taking into the consideration only the magnitude of each word count (tf-idf) of each document, but the angle between the documents. What we have to do to build the cosine similarity equation is to solve the equation of the dot product for the \cos{\theta}:
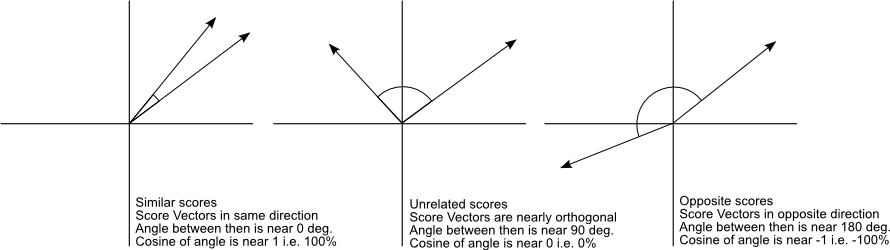
And that is it, this is the cosine similarity formula. Cosine Similarity will generate a metric that says how related are two documents by looking at the angle instead of magnitude, like in the examples below:
Note that even if we had a vector pointing to a point far from another vector, they still could have an small angle and that is the central point on the use of Cosine Similarity, the measurement tends to ignore the higher term count on documents. Suppose we have a document with the word “sky” appearing 200 times and another document with the word “sky” appearing 50, the Euclidean distance between them will be higher but the angle will still be small because they are pointing to the same direction, which is what matters when we are comparing documents.
input.txt -> urls of webpages to be compared
output.txt -> resulting matrix