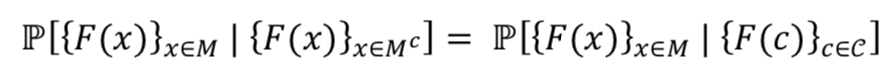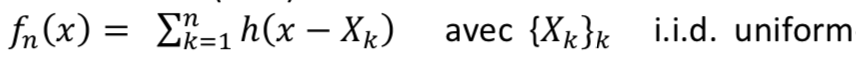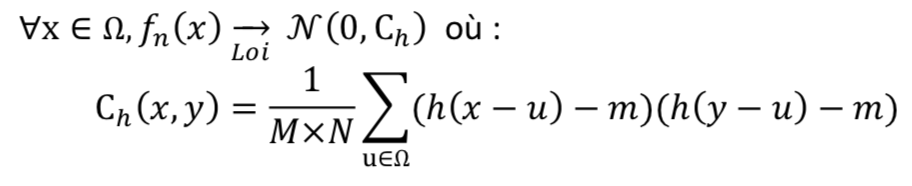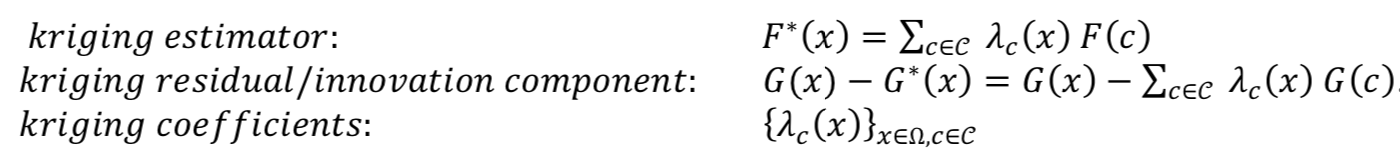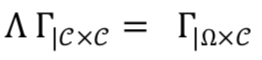We implemented the inpainting method for texture images introduced in
Microtexture inpainting through gaussian conditional simulation, Bruno Galerne, Arthur Leclaire, Lionel Moisan
Inpainting is the task of recovering a missing region of an image. This region is called a masked region. The paper we followed propose an inpainting method in the case of texture images. In this framework texture images are supposed to be a random gaussian field. Authors used the work of Julesz, on the translation invariance of texture images statistics of order 1 and 2, to model and estimate the variance of this gaussian vector. Masked region is then recovered by conditional simulation.
We model our pixels grid as a Markov random field. Markov property states that:
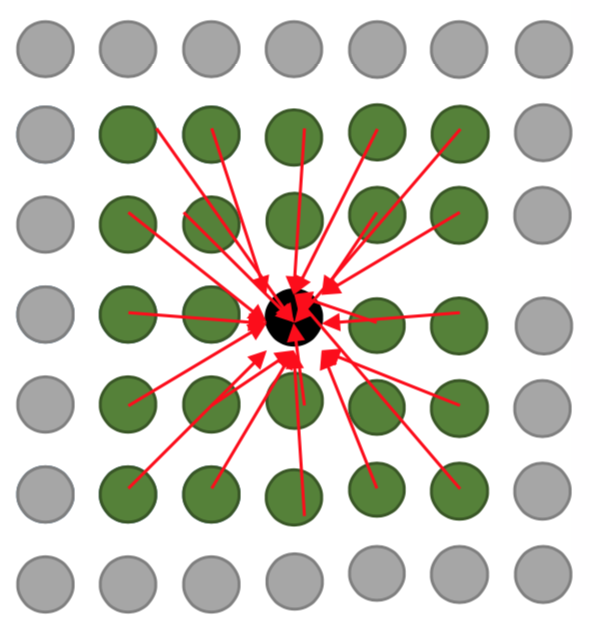
We will use the Markov blanket around the masked region in order to infer inpainted region (recovered region). Here is an example of a Markov blanket of one pixel in a Markov random field.
Following Julesz's theory it is assumed that statistics of order 1 and 2 are translation invariant in the case of texture images.
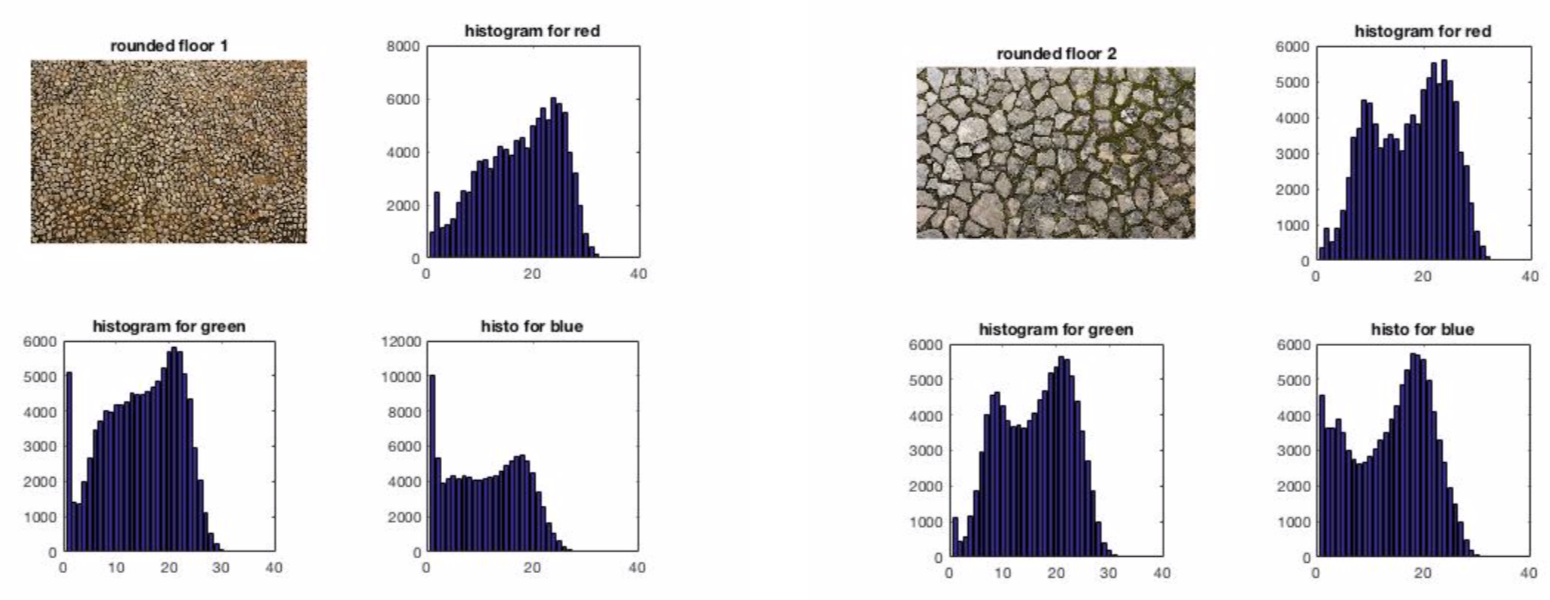
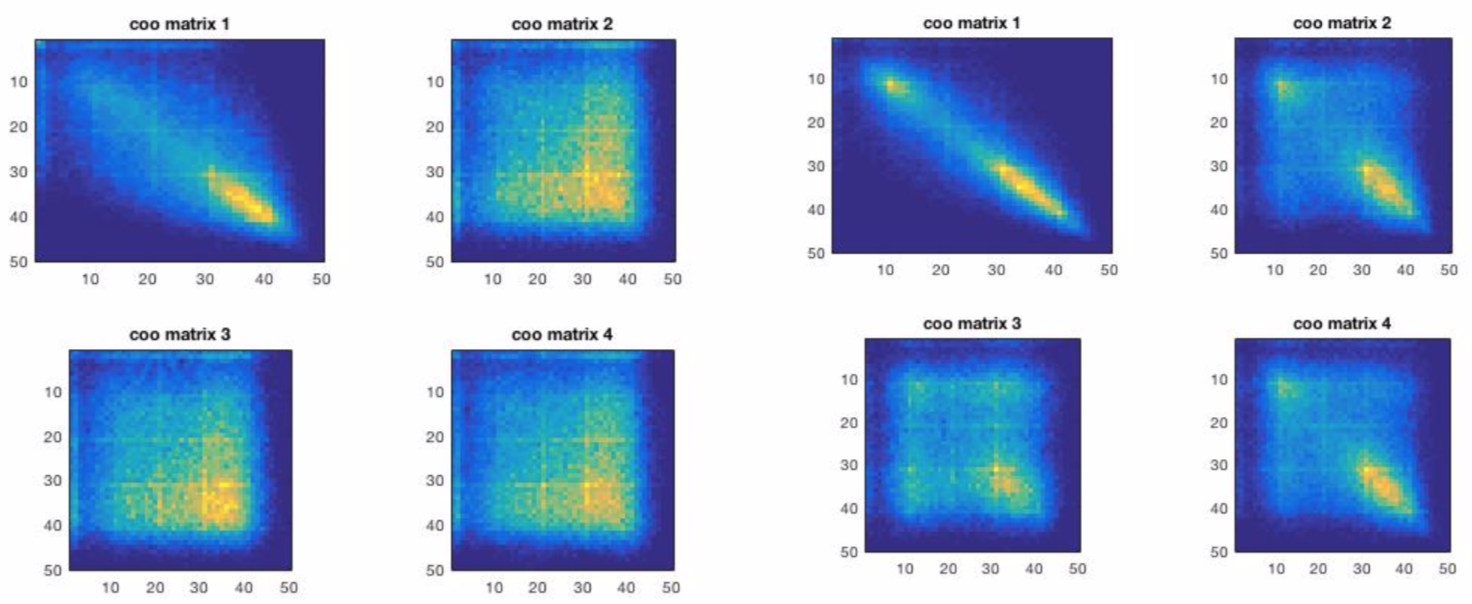
Here is an example where we compared statistics of order 1 and 2 for two images of pebbles. We can notice the similarity of pixel statistics for these two images.
Starting from a Discret Spot Noise (DSN) we can generate texture image by using the model:
We have the theorical guarantee from Central Limit Theorem that asymptotically it will follow a gaussian distribution. Hence we have the following result:
Therefore we notice that we obtain a stationary gaussian process.
In the following we used this model to sample a texture image of paper by consecutive translation of spot noise (small patch from texture image).
Finally we want to sample H = F* + G - G* where G ~ F and G independant of F. We will sample the kriging estimator F* and the kriging residual or innovation component G - G* using the kriging coefficients. In summary:
And to compute the kriging coefficients we need to solve the kriging system:
where:
Without further ado here are our results:
Here we noticed that it does not work since texture image contains too much structure. Hence it does match the invariance assumptions. Indeed we failed to sample a good DSN:
Although the texture is so structured we could recover the missing region just by using the kriging estimator and we got a perfect result.
Obvious case of failure. Texture image contrains a highly complex structure. We are out of our framework.