Simplified version of the Facebook Prophet model re-implemented in PyMC3. Note that PMProphet only supports the full bayesian estimation through MCMC (more precisely it uses PyMC3). Note also that this is still an early version and it might definitely contain code and/or conceptual bugs.
To install:
pip install pmprophet
What's implemented:
- Nowcasting & Forecasting
- Intercept, growth
- Regressors
- Holidays
- Additive seasonality
- Fitting and plotting
- Custom choice of priors (not included in the original prophet)
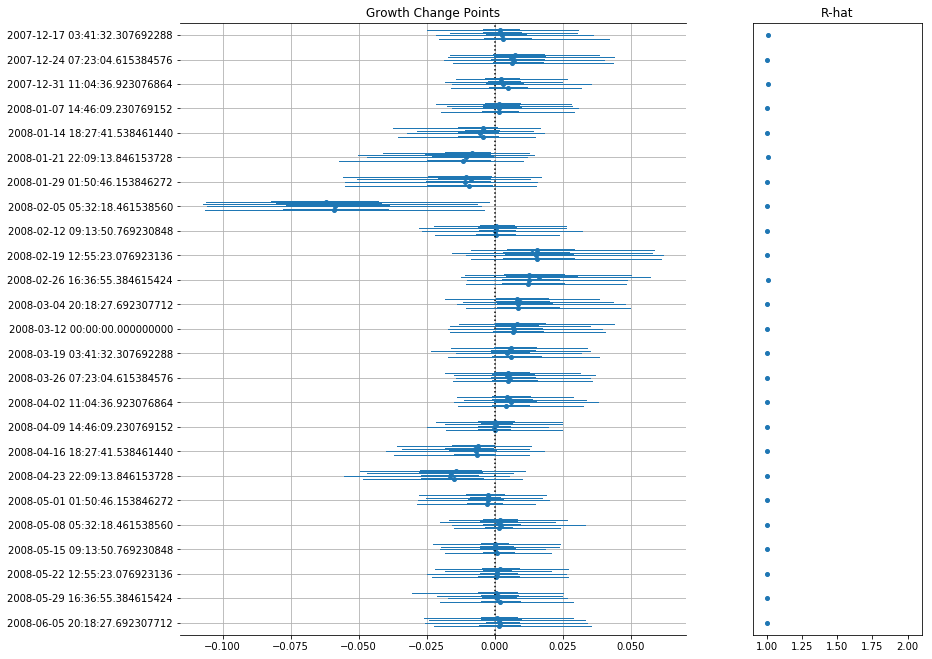
- Changepoints in growth
- Fitting with NUTS/AVDI/Metropolis
What's not yet implemented w.r.t. Facebook Prophet:
- Multiplicative seasonality
- Saturating growth
- Uncertainty is not exactly estimated 1:1
- Timeseries with non daily frequencies are untested (thus unlikely to work)
- (potentially other things)
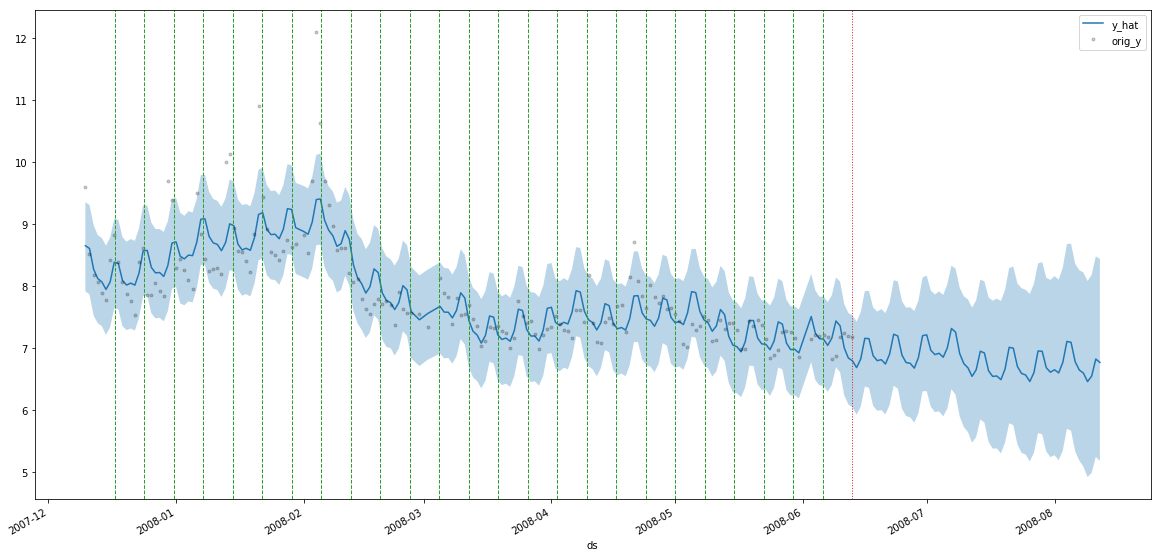
Predicting the Peyton Manning timeseries:
import pandas as pd
from PMProphet.model import PMProphet
df = pd.read_csv("examples/example_wp_log_peyton_manning.csv")
df = df.head(180) # Only keep the first 180 days of data
# Fit both growth and intercept
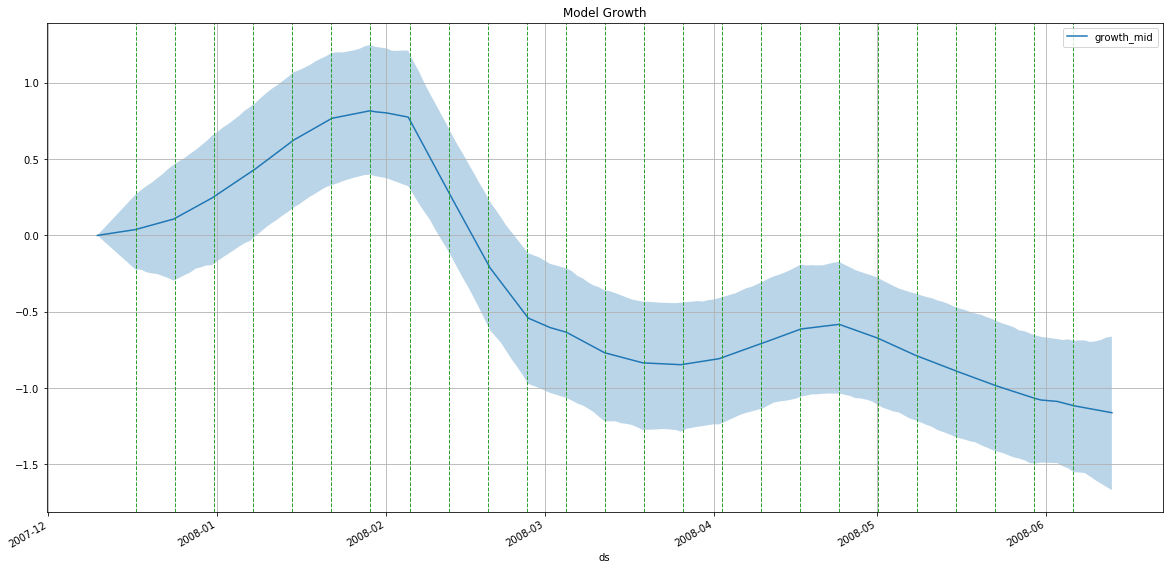
m = PMProphet(df, growth=True, intercept=True, n_change_points=2, name='model')
# Add monthly seasonality (order: 3)
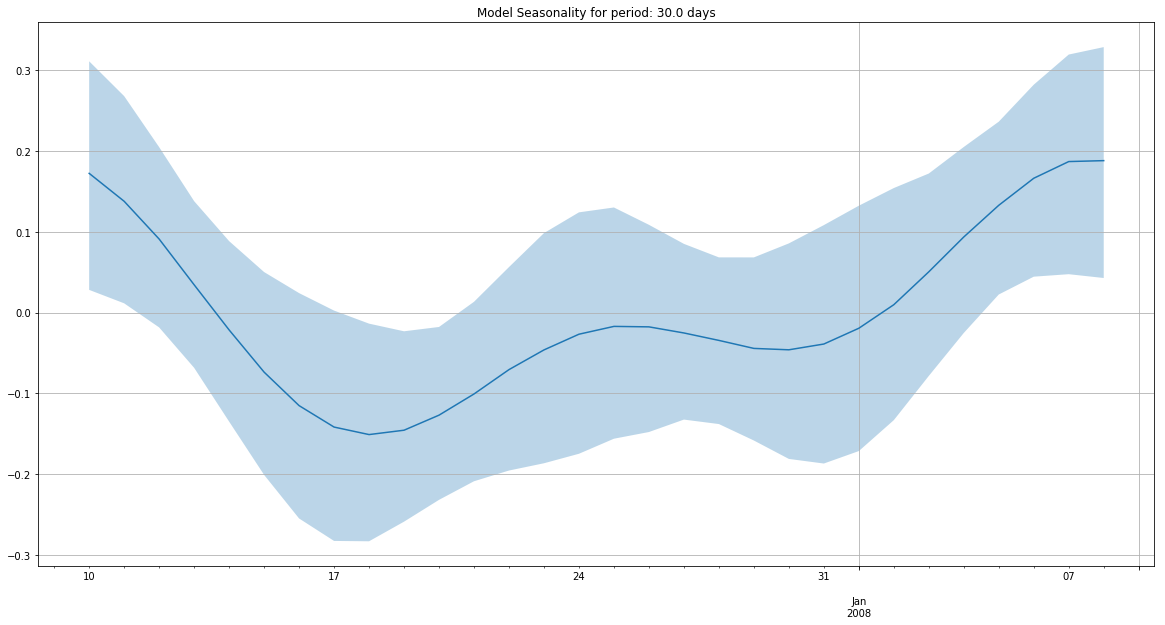
m.add_seasonality(seasonality=30, order=3)
# Add weekly seasonality (order: 3)
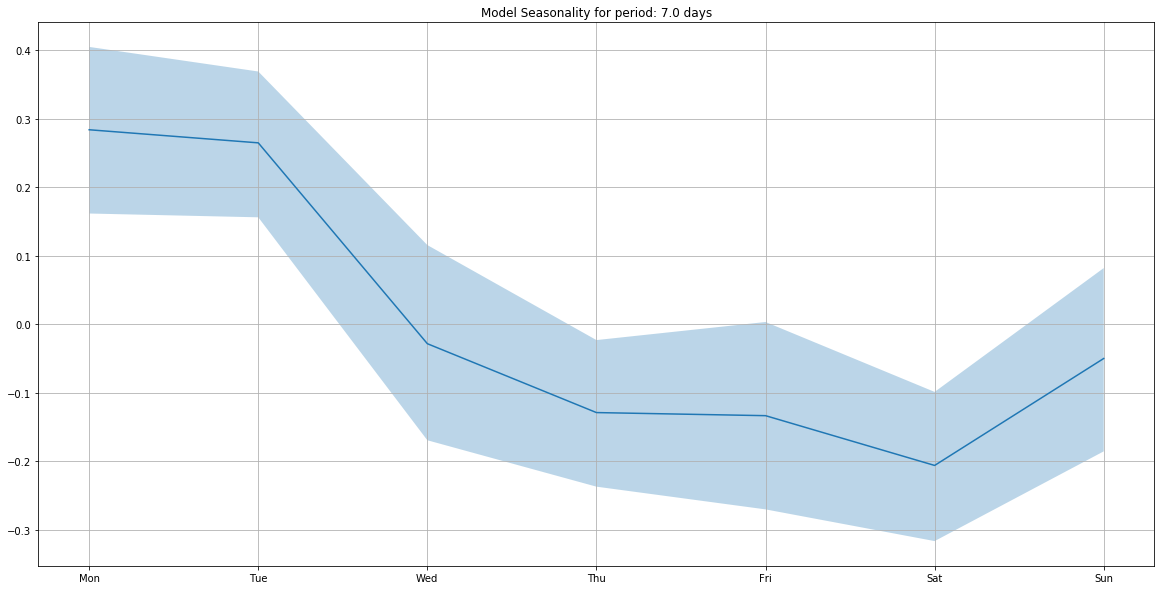
m.add_seasonality(seasonality=7, order=3)
# Fit the model (using NUTS, 1e+4 samples and no MAP init)
m.fit(
draws=10**4,
method='NUTS',
map_initialization=False,
)
ddf = m.predict(100, alpha=0.4, include_history=True, plot=True)
m.plot_components(
intercept=False,
)One of the main reason why PMProphet was built is to allow custom priors for the modeling.
The default priors are:
| Variable | Prior | Parameters |
|---|---|---|
regressors |
Normal | loc:0, scale:10 |
holidays |
Laplace | loc:0, scale:10 |
seasonality |
Laplace | loc:0, scale:1 |
growth |
Laplace | loc:0, scale:10 |
changepoints |
Laplace | loc:0, scale:10 |
intercept |
Normal | loc:y.mean, scale: 2 * y.std |
sigma |
Half Cauchy | loc:100 |
But you can change model priors by inspecting and modifying the distribution in
m.priorswhich is a dictionary of {prior: pymc3-distribution}.
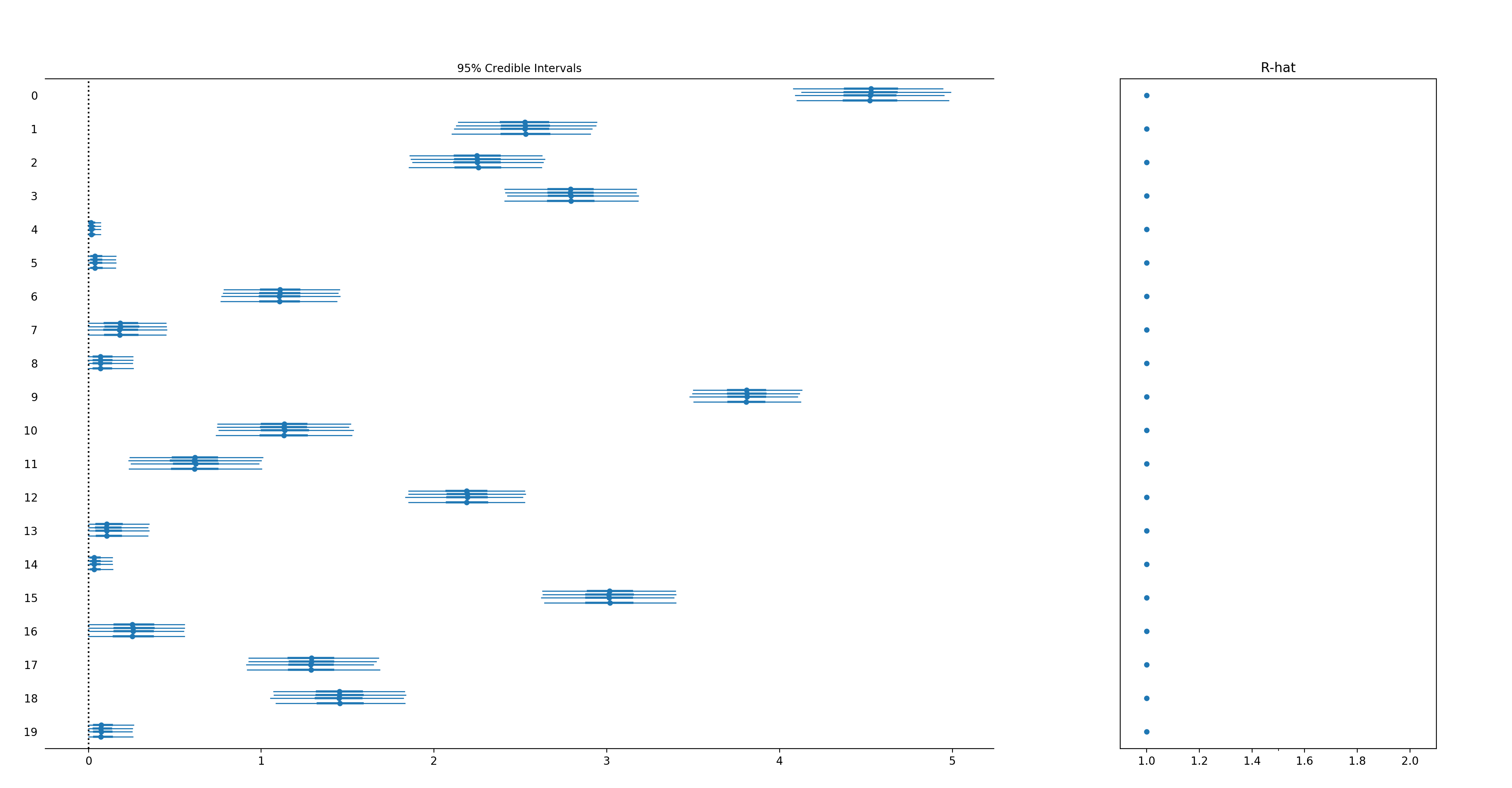
In the example below we will model an additive time-series by imposing a "positive coefficients" constraint by using an Exponential distribution instead of a Laplacian distribution for the regressors.
import pandas as pd
import numpy as np
import pymc3 as pm
n_timesteps = 100
n_regressors = 20
regressors = np.random.normal(size=(n_timesteps, n_regressors))
coeffs = np.random.exponential(size=n_regressors) + np.random.normal(size=n_regressors)
# Note that min(coeffs) could be negative due to the white noise
regressors_names = [str(i) for i in range(n_regressors)]
df = pd.DataFrame()
df['y'] = np.dot(regressors, coeffs)
df['ds'] = pd.date_range('2017-01-01', periods=n_timesteps)
for idx, regressor in enumerate(regressors_names):
df[regressor] = regressors[:, idx]
m = PMProphet(df, growth=False, intercept=False, n_change_points=0, name='model')
with m.model:
# Remember to suffix _<model-name> to the custom priors
m.priors['regressors'] = pm.Exponential('regressors_%s' % m.name, 1, shape=n_regressors)
for regressor in regressors_names:
m.add_regressor(regressor)
m.fit(
draws=10 ** 4,
method='NUTS',
map_initialization=False,
)
m.plot_components()