/hilbert-matrix

Various numerical analysis methods to solve a linear system of equations with coeff matrix being the Hilbert matrix.

Primary LanguageJulia

hilbert-matrix

Various numerical analysis methods for solving a linear system of equations involving the Hilbert Matrix.

The problem

Basically, we simply want to solve for $x$ the following system:

$$ Hx=b $$

Where $H$ is the $n \times n$ Hilbert matrix given by the rule

$$ h_{ij} = \frac{1}{i + j - 1} $$

And $b \in \mathbb{R}^{n}$ the vector given by

$$ b = (1 \quad 1 \quad 1 \quad ... \quad 1)^{T} $$

  • In this implementation, we will fix the order of $n$ to be 100.

The main metric used in this project is the Relative residual norm given by:

$$ || r_{rel} || = \frac{|| b - Hx ||}{|| b ||} $$

Methods

In this project, we implemented the following methods for aproximating the solution:

  • LU decomposition
  • Cholesky decomposition
  • Jacobi Over-Relaxation (JOR)
  • Successive Over-Relaxation (SOR)
  • Gradient Ascent
  • Conjugate Gradient

All methods are implemented from scratch.

Results

LU decomposition

Since LU is a relatively stable direct method for Symmetric Positive Definite (SDP) matrices, we can check the relative residual norm at each order $n$ compared to the desired tolerance

Cholesky decomposition

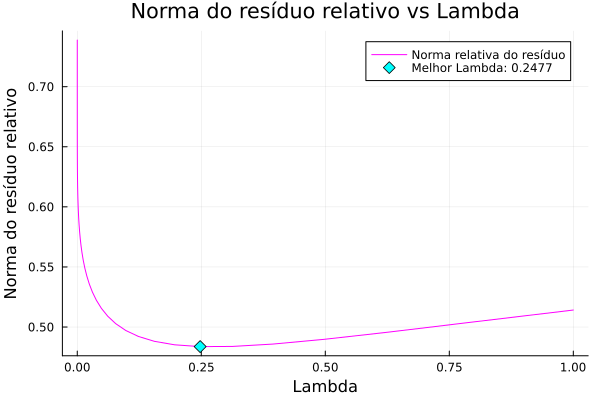
Overall, this is the best method for SDP matrices. However, due to the bad conditioning of $H$, the floating-point errors acumulate so much it looks like the $H$ decomposition lose its "positiveness" or something.

In order to prevent this, we can create a new aproximated matrix. We just need to add small values $\lambda$ to the diagonal of $H$ and see what reduces the relative residual norm the most:

JOR

Since $H$ is SDP, we can get the optimal $\omega$ in a closed form, but it does not work since, again, it is bad conditioned.

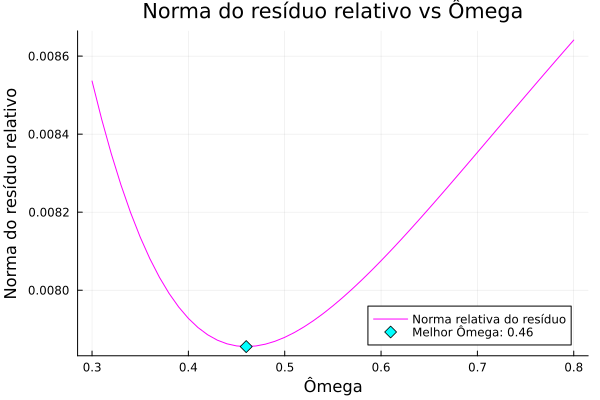
So we can simply iterate over various $\omega$ values and find the optimal one by brute force.

SOR

Same thing as JOR, simply iterate over all possible $\omega$.

Gradient Ascent

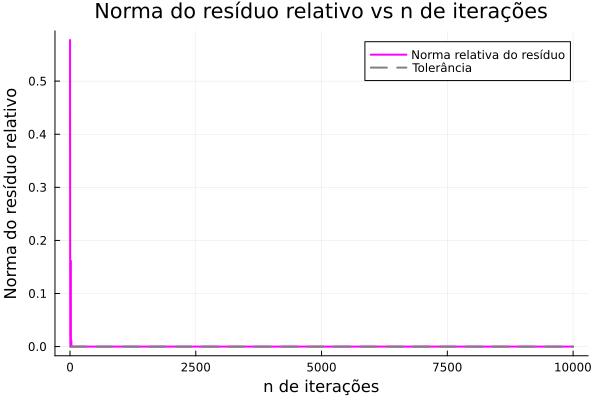
A really good family of methods are the iterative methods around the gradient. Deriving from optimization, the method converges really fast to an acceptable tolerance, but struggles to reach a good score.

Conjugate Gradient

The theory AND the performace are INSANE, literaly SMASHED the other methods. In just 30 iterations it reached the desired tolerance of 1e-7. Absolute beast.

References