Sayuri Takeda Junho de 2018
O objetivo deste trabalho será detectar fraudes na base Credit Card Fraud Detection do Kaggle demonstrando alguns classificadores.
Inicialmente iremos fazer uma análise exploratória dos dados afim de estudar como a base se comporta.
Em seguida iremos rodar os algoritmos regressão logistica, redes neurais e adaboosting calculando a sensibilidade para cada método, lembrando que, quanto maior a sensibidade melhor.
A base contém 31 colunas, sendo a coluna Time os segundos no período de 2 dias.
## Time V1 V2 V3 V4 V5 V6
## 1 0 -1.3598071 -0.07278117 2.5363467 1.3781552 -0.33832077 0.46238778
## 2 0 1.1918571 0.26615071 0.1664801 0.4481541 0.06001765 -0.08236081
## 3 1 -1.3583541 -1.34016307 1.7732093 0.3797796 -0.50319813 1.80049938
## 4 1 -0.9662717 -0.18522601 1.7929933 -0.8632913 -0.01030888 1.24720317
## 5 2 -1.1582331 0.87773675 1.5487178 0.4030339 -0.40719338 0.09592146
## 6 2 -0.4259659 0.96052304 1.1411093 -0.1682521 0.42098688 -0.02972755
## V7 V8 V9 V10 V11 V12
## 1 0.23959855 0.09869790 0.3637870 0.09079417 -0.5515995 -0.61780086
## 2 -0.07880298 0.08510165 -0.2554251 -0.16697441 1.6127267 1.06523531
## 3 0.79146096 0.24767579 -1.5146543 0.20764287 0.6245015 0.06608369
## 4 0.23760894 0.37743587 -1.3870241 -0.05495192 -0.2264873 0.17822823
## 5 0.59294075 -0.27053268 0.8177393 0.75307443 -0.8228429 0.53819555
## 6 0.47620095 0.26031433 -0.5686714 -0.37140720 1.3412620 0.35989384
## V13 V14 V15 V16 V17 V18
## 1 -0.9913898 -0.3111694 1.4681770 -0.4704005 0.20797124 0.02579058
## 2 0.4890950 -0.1437723 0.6355581 0.4639170 -0.11480466 -0.18336127
## 3 0.7172927 -0.1659459 2.3458649 -2.8900832 1.10996938 -0.12135931
## 4 0.5077569 -0.2879237 -0.6314181 -1.0596472 -0.68409279 1.96577500
## 5 1.3458516 -1.1196698 0.1751211 -0.4514492 -0.23703324 -0.03819479
## 6 -0.3580907 -0.1371337 0.5176168 0.4017259 -0.05813282 0.06865315
## V19 V20 V21 V22 V23
## 1 0.40399296 0.25141210 -0.018306778 0.277837576 -0.11047391
## 2 -0.14578304 -0.06908314 -0.225775248 -0.638671953 0.10128802
## 3 -2.26185710 0.52497973 0.247998153 0.771679402 0.90941226
## 4 -1.23262197 -0.20803778 -0.108300452 0.005273597 -0.19032052
## 5 0.80348692 0.40854236 -0.009430697 0.798278495 -0.13745808
## 6 -0.03319379 0.08496767 -0.208253515 -0.559824796 -0.02639767
## V24 V25 V26 V27 V28 Amount Class
## 1 0.06692807 0.1285394 -0.1891148 0.133558377 -0.02105305 149.62 0
## 2 -0.33984648 0.1671704 0.1258945 -0.008983099 0.01472417 2.69 0
## 3 -0.68928096 -0.3276418 -0.1390966 -0.055352794 -0.05975184 378.66 0
## 4 -1.17557533 0.6473760 -0.2219288 0.062722849 0.06145763 123.50 0
## 5 0.14126698 -0.2060096 0.5022922 0.219422230 0.21515315 69.99 0
## 6 -0.37142658 -0.2327938 0.1059148 0.253844225 0.08108026 3.67 0
A base é bem desbalanceada, apenas 0.17% da base são fraudes.
Abaixo segue tabela com montante em classes e percentual de fraudes para cada classe:
| montante\_classe | 0 | 1 | percentual\_fraudes |
|---|---|---|---|
| \[0, 10) | 97065 | 249 | 0.25652913 |
| \[10, 100) | 129995 | 113 | 0.08692642 |
| \[100, 1,000) | 54195 | 121 | 0.22326783 |
| \[1,000, 10,000) | 3052 | 9 | 0.29488860 |
| \[10,000, 100,000\] | 8 | 0 | 0.00000000 |
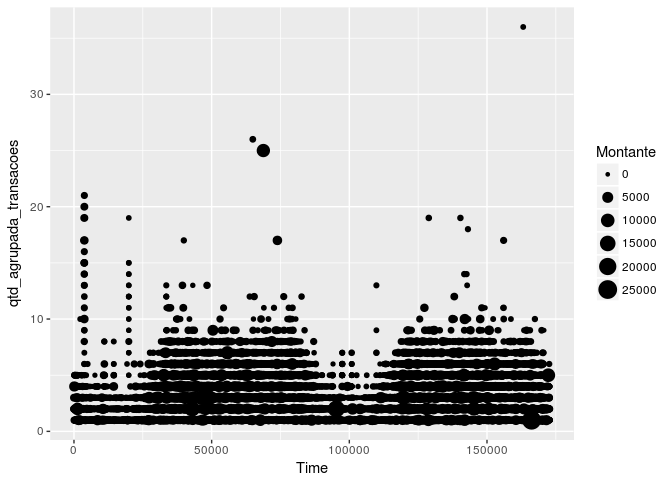
Com o seguinte gráfico podemos inferir que existem menos fraudes no começo dos dias:
Agora tentaremos encontrar algum padrão:
Podemos perceber que nenhuma variável segue o tempo:
Algumas variáveis seguem V1:
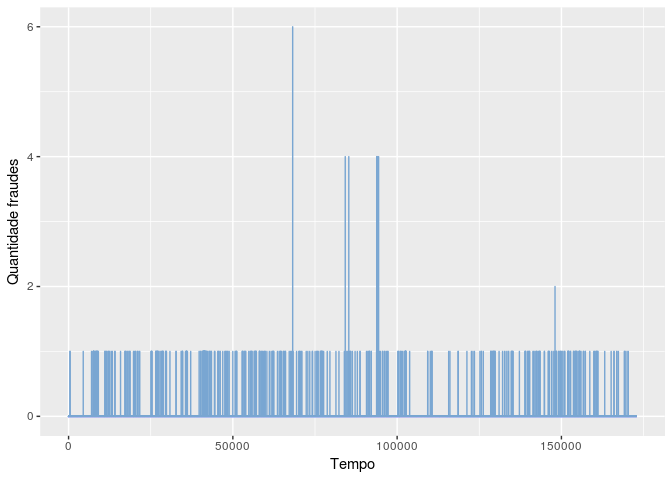
Plotando o gráfico abaixo podemos perceber que ao longo do tempo (segundos) existem alguns picos mas a maior parte das ocorrencias são iguais a 1, ou seja, as fraudes aparentemente estão bem distribuidas:
Iremos separar em treino e teste.
treino <- createDataPartition(y = base$Class, p =0.80, list = F)
base_treino_inteira <- base[treino,]
base_teste <- base[-treino,]A base_treino_inteira que contém 80% dos dados será dividida em treino e validação e o teste será rodado apenas no fim de tudo.
inTrain <- createDataPartition(y = base_treino_inteira$Class, p =0.80, list = F)
base_treino <- base_treino_inteira[inTrain,]
base_validacao <- base_treino_inteira[-inTrain,]Será calculada a sensibilidade que é a capacidade de acertar fraude dado que é fraude, ou seja, são os positivos verdadeiros dividido pela soma dos positivos verdadeiros mais positivos falsos.
Iremos rodar a regressão 5x e tirar a média das sensibilidades:
## [1] 0.6385542 0.5365854 0.6206897 0.6206897 0.6756757
A sensibilidade para regressão logistica será a média das 5x:
## [1] 0.6184389
Podemos ver os pesos para cada árvore:
## [1] 3.823449 3.295894 3.002821 3.023511 2.781831
E olhar a matriz de confusão:
##
## 0 1
## 0 45483 3
## 1 17 66
Dessa maneira podemos calcular a sensibilidade:
## [1] 0.7951807
Primeiro faremos uma feature engineering, criaremos uma coluna para classe 0 e outra para classe 1, quando ocorrer a fraude a linha da coluna classe 1 irá conter o valor 1.
Em seguida rodaremos o modelo com a base treino e faremos o predict com a base validação para calcularmos a sensibilidade.
Tabela com resultados:
## # weights: 299
## initial value 94306.403673
## iter 10 value 638.095073
## iter 20 value 637.193192
## iter 30 value 630.689551
## iter 40 value 630.118010
## iter 50 value 629.458526
## iter 60 value 629.116640
## iter 70 value 628.930882
## iter 80 value 628.928561
## iter 90 value 628.921472
## iter 100 value 628.920403
## iter 110 value 628.616396
## iter 120 value 620.985690
## iter 130 value 393.735152
## iter 140 value 384.062597
## iter 150 value 257.155540
## iter 160 value 252.926827
## iter 170 value 252.654224
## iter 180 value 251.140816
## iter 190 value 245.798736
## iter 200 value 220.560719
## final value 220.560719
## stopped after 200 iterations
##
## 0 1
## 0 45479 5
## 1 18 66
## [1] 0.7857143
Podemos plotar a rede:
Encontramos as seguintes sensibilidades:
sensibilidade_reglog## [1] 0.6184389
sensibilidade_adaboosting## [1] 0.7951807
sensibilidade_nnet## [1] 0.7857143