Quantum computing examples with QISKit.
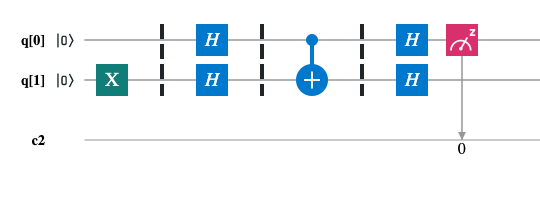
Problem. For given an oracle function f : {0, 1} -> {0, 1}, determine f is balanced or constant.
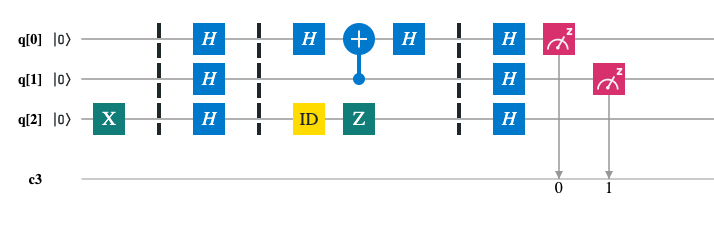
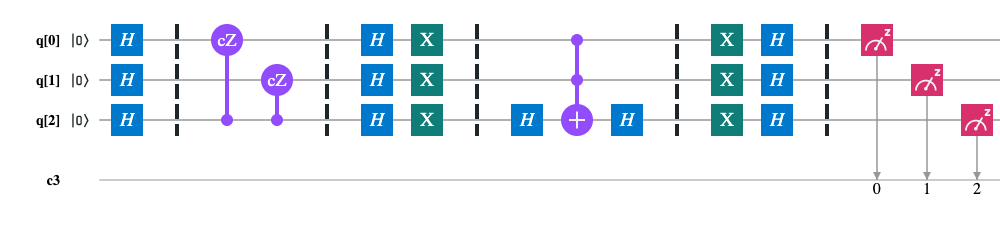
Problem. For given an oracle function f : {0, 1}^n -> {0, 1}, determine f is balanced or constant.
Scheme for n=2:
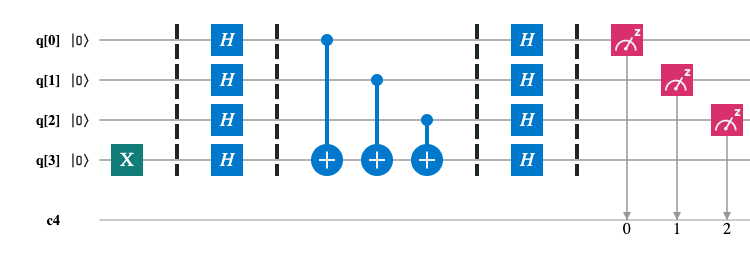
Problem. For given an oracle function f : {0, 1}^n -> {0, 1}, f(x) = a x, determine a.
Scheme for n=3:
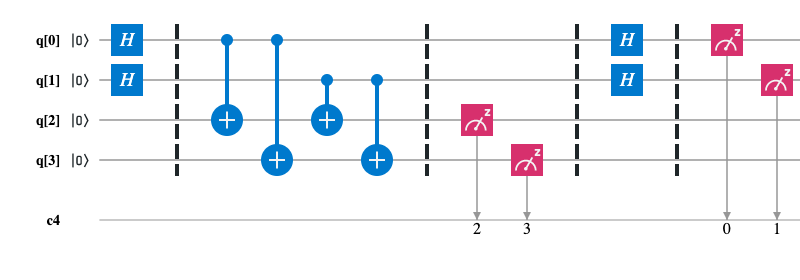
Problem. For given an oracle function f : {0, 1}^n -> {0, 1}^n which has period
a: ∃!a != 0: ∀x f(x) = f(y) => y = x ⊕ a. Determine a.
Scheme for n=2:
Scheme for n=3:
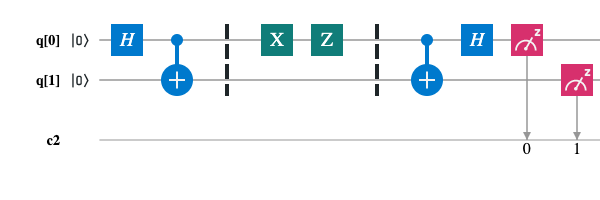
Task. Transmit two bits of classical information between Alice and Bob using only one qubit.
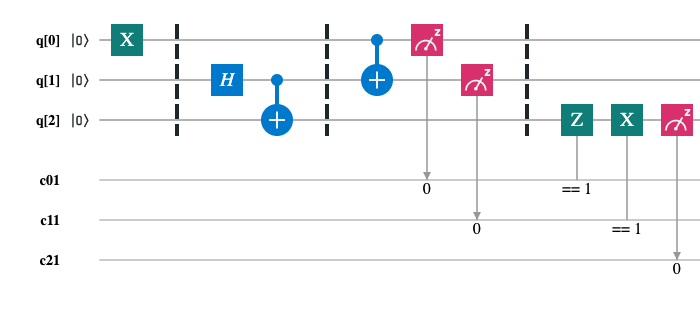
Task. Alice would like to send Bob a qubit that is in some unknown state.
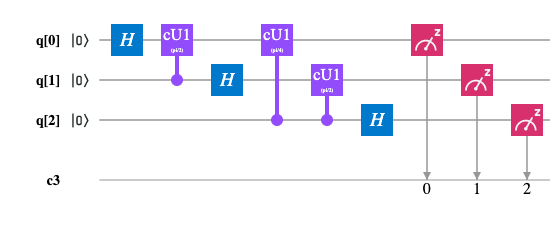
Problem. Given an unitary operator U, estimate θ in U|ψ>=exp(2πiθ)|ψ>.
Problem. For given an oracle function f : {0, 1}^n -> {0, 1}^n, ∃! ω : f(ω) = a, find ω.
Scheme for n=3:
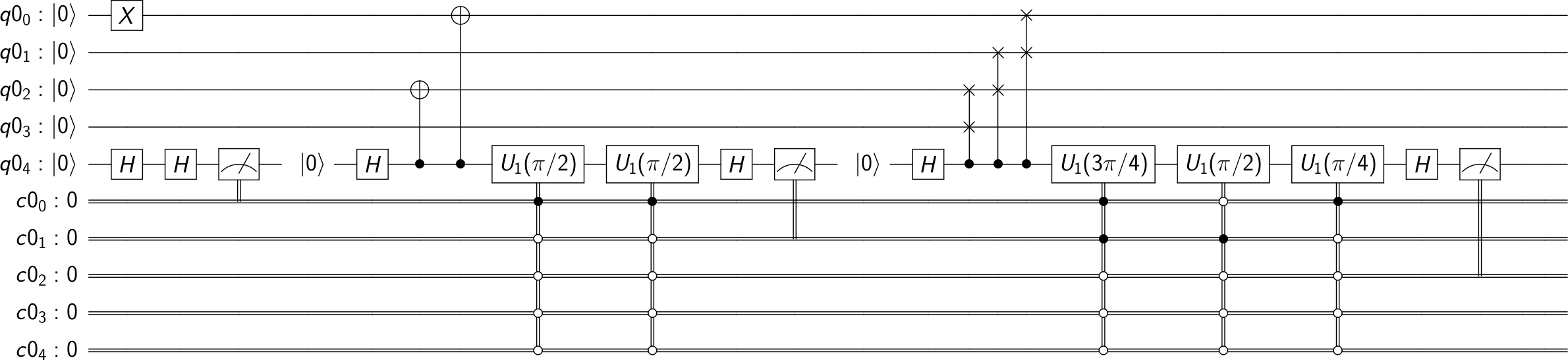
Problem. Shor's algorithm is a quantum computer algorithm for integer factorization. Informally, it solves the following problem: Given an integer N, find its prime factors.
Scheme for find the period r for f(x) = 2^x mod 15:
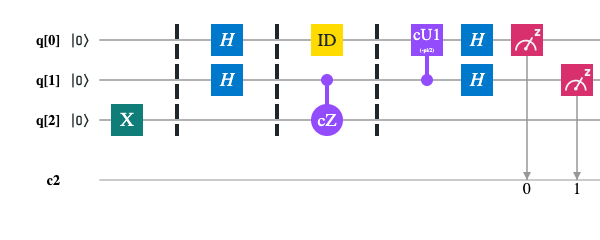
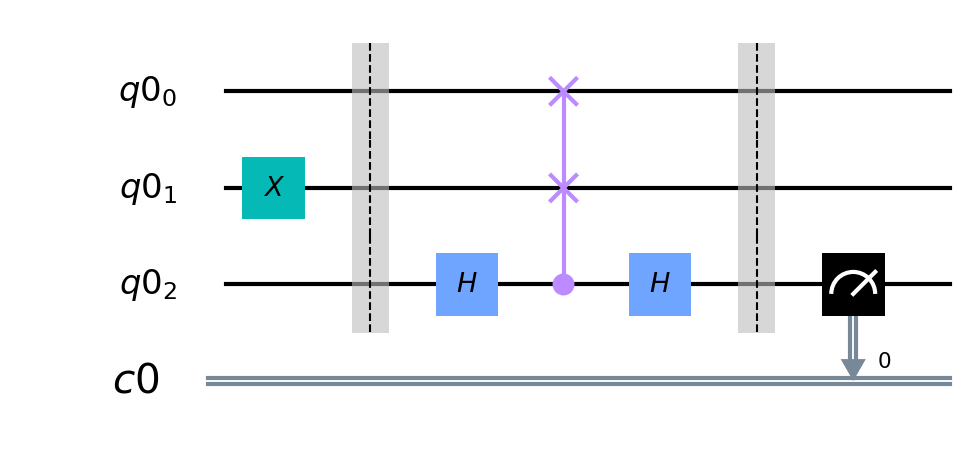
Task. For given two unknown quantum states, determine how much them differs.