This project builds an EEG circuit which will allow the user to send morse code to a computer through their brain wave activity. It is a basic form of “mind reading” and has applications in helping paralyzed people who can not speak or write. The circuit amplifies electrical signals from the brain and uses various high and low pass analog filters. We then post-process the data using digital filters, statistical methods, and Single Component analysis. We hope to demonstrate the successful communication of words in a timely manner through brainwave data. The biggest challenge is that an EEG which measures voltage differences across your scalp can produce noisy and sometimes unreliable signals, so careful filtering and project design must be done. Our general approach is to distinguish between two mental states with the EEG, whether a person is relaxed (alpha waves, 8-12Hz) or if they are concentrating / alert (beta waves, 12-30Hz). The user can then switch between these two mental states over time signaling a beep or no beep to communicate in morse code. We will use the following link as a starting point (found on instructables.com/DIY-EEG-and-ECG-Circuit/).
EEG stands for electroencephalogram. It measures voltage fluctuations resulting from ionic current within the neurons of the brain. Neurons exchange ions with environment and when many ions are pushed out of many neurons at the same time, they repel and push each other forming a wave. The waves reaches scalp and can be captured by the electrodes. Note that EEG does not capture the activities of single neurons-the electric potential is way to small to be captured. Instead, EEG measures the voltage difference in 2 electrodes over time, which reflect synchronized activity over a network of neurons. Spatially well-aligned neurons fire together, so the electrode placements need to be in specific regions to observe oscillations/waves of interest. These waves have different characteristic frequency, magnitude, and are related to different brain activties.
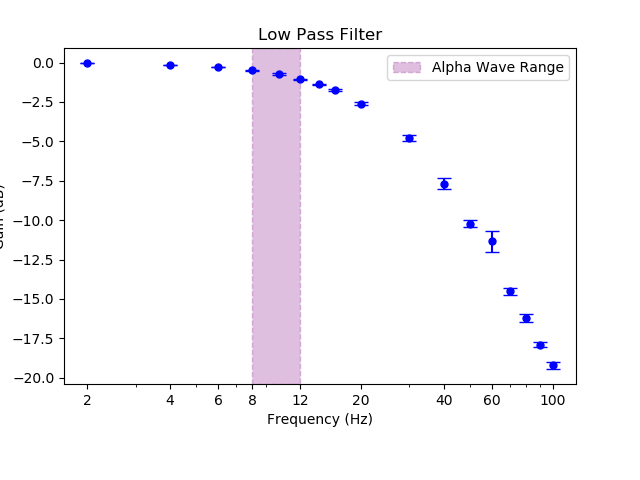
In our project, we measure alpha waves originating from the occipital lobe because they are one of the strongest EEG signals. Alpha waves have a signature frequency in the range of 8-12 HZ. Alpha waves are reduced with open eyes, drowsiness, and sleep. It is still under study but main stream research shows it represent the activity of the visual cortex in an idle state. In theory, our circuit also has the capacity to measure beta waves (12-30 HZ).
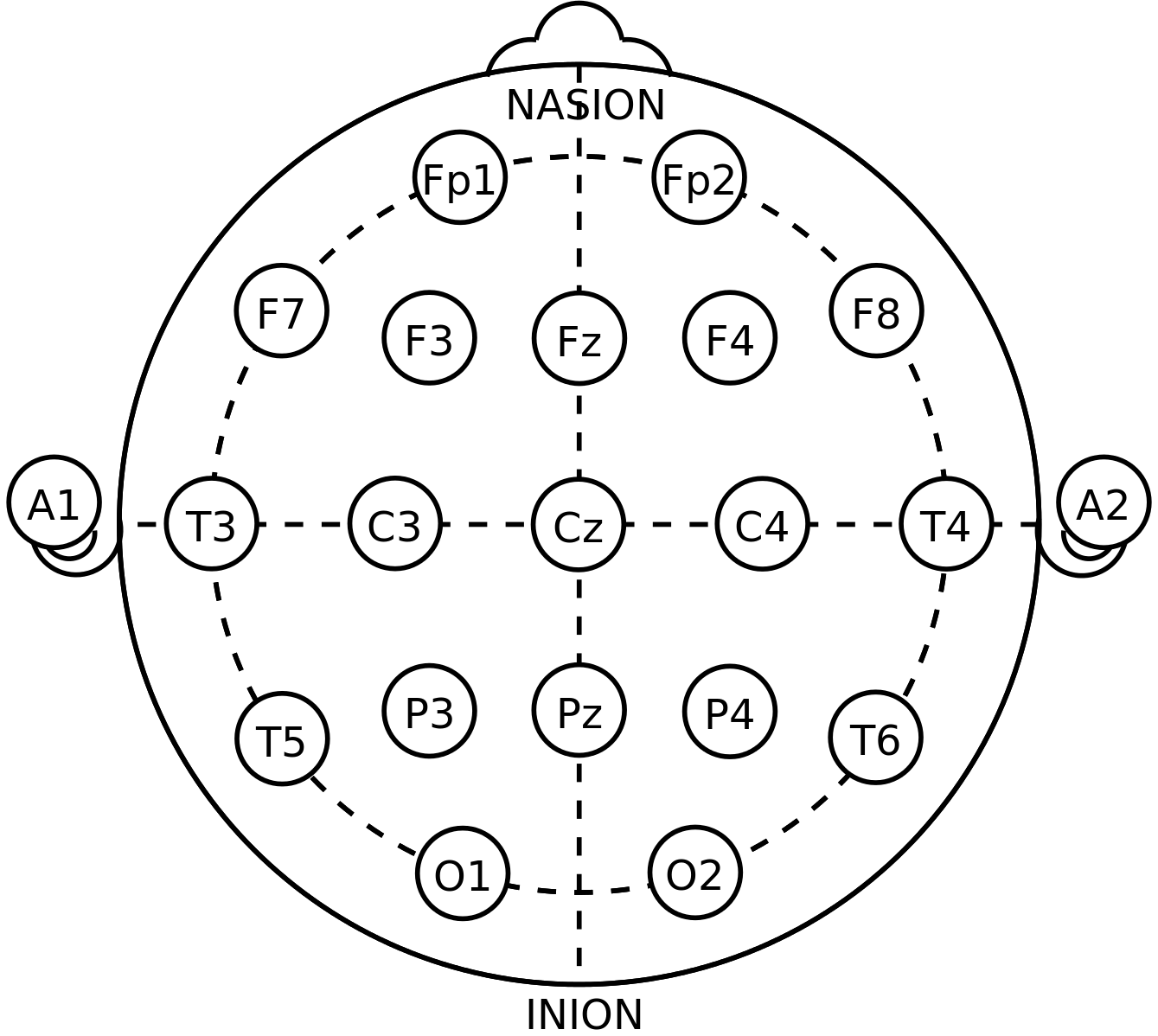
There are many possible electrode placements depending on what wave one choose to measure. In our project, we measure alpha waves We need to use three electrode: one at the left mastoid (the bone at the back of the left ear) which is connected to the ground of the circuit; one located one inch above and one inch right of the nasion (the midline bony depression between the eyes where the frontal and two nasal bones meet); the last one located one inch above and one inch right of the inion (the projecting part of the occipital bone at the base of the skull). The 2nd and 3rd electrode placements are approximately in O2 and Fp2 regions in the below diagram:
The voltage difference oscillations between the 2nd and 3rd electrodes are the target alpha waves, which is then fed to the circuit to be amplified, filtered, and analyzed.
- Raspberry Pi 4
- TDE-2143-C EEG Gold Cup Electrodes
- Electrode gel, tape
- Instrumental Amplifier AD622ANZ
- Quad Operational Amplifier TL084x
- Potentiometer CT6EW102-ND, 1kOhm
- Capacitors and Resistors
- two 9V batteries
- Bread board and wires
- Open Scope MZ (Used as oscilloscope and wave generator for testing circuit only)
- ADDDDDDDDD ADC!!!!!
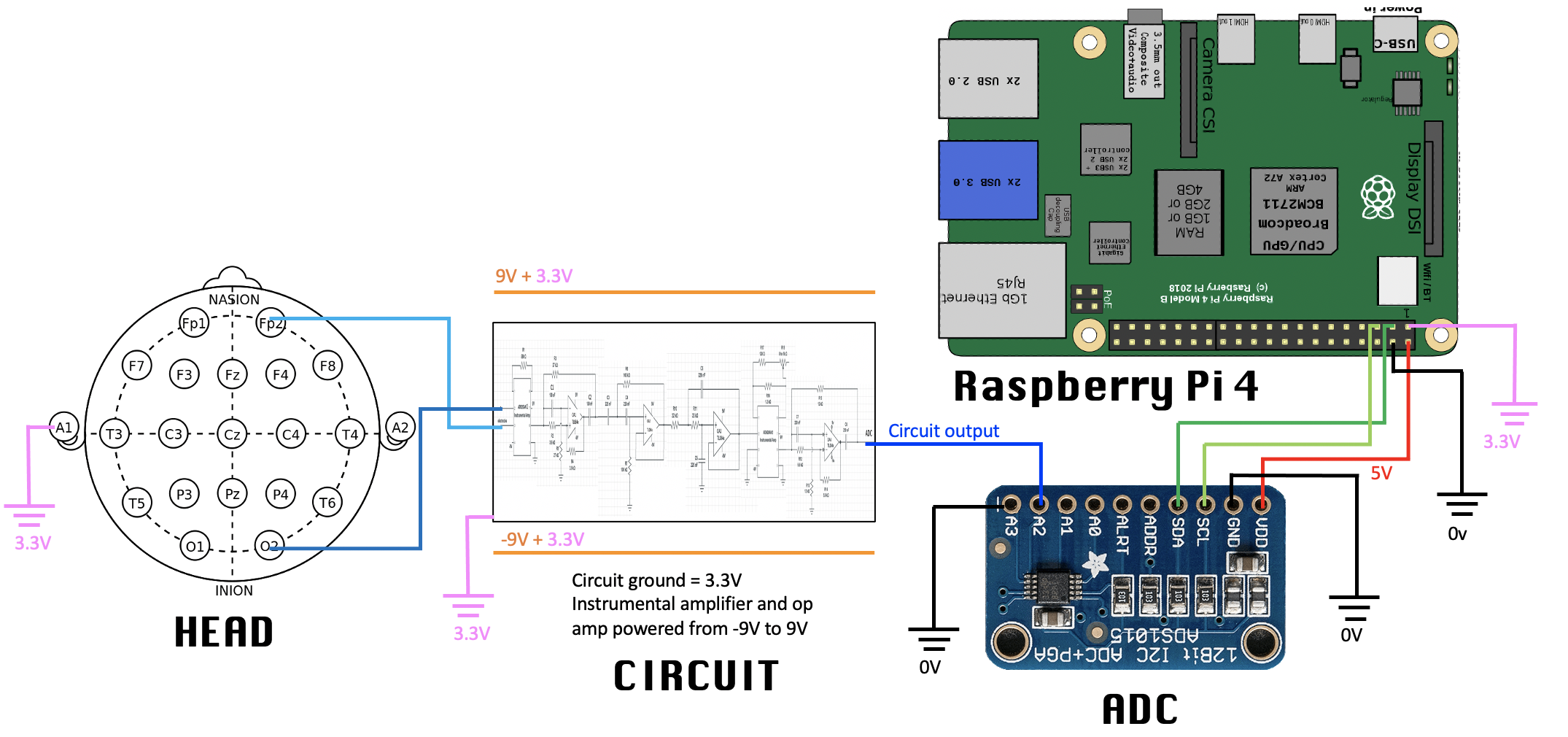
The above diagram describes the complete EEG setup. The user tapes 3 electrodes to their scalp at various locations to measure the brain's electrical signals. These elcetrodes are attached to the circuit, which serves to amplify alpha waves and filter out other signals. The voltage output of the circuit is measured with the ADC and the data is sent to the Rpi. The Rpi applies further digital filtering and outputs the voltage of the user's alpha waves.
Note that we have two different grounds; the ADC and Rpi ground (black) at 0V, and the circuit ground (pink) at 3.3V. This design choice is due to ADC input voltage limitations and is explained in detail later. To get the -9V to 9V of power with respect to the 3.3V ground, connect one 9V battery the correct way, and the other one backwards.
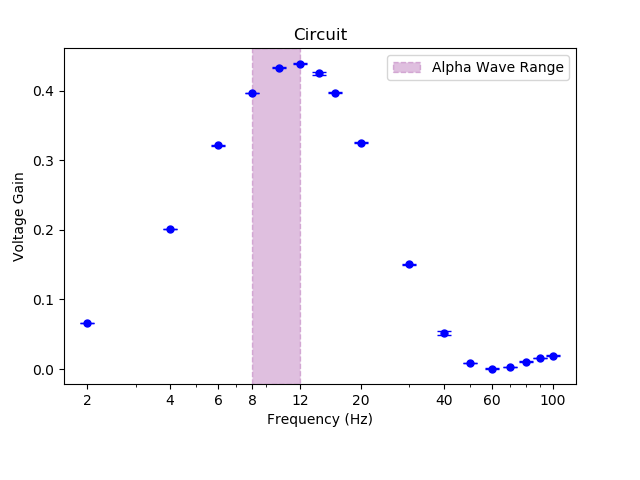
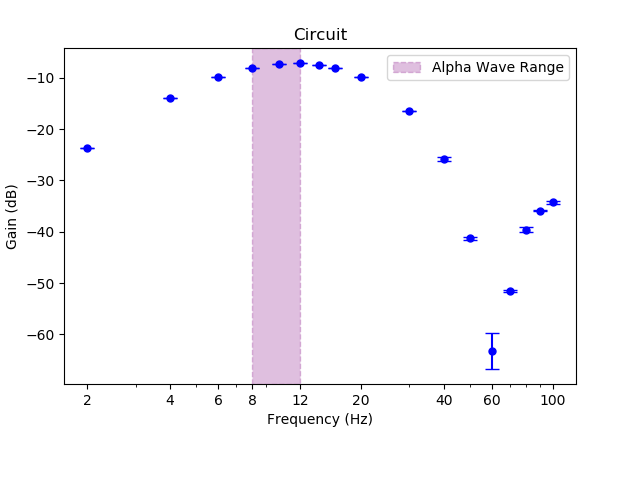
The circuit consist of the following sections:
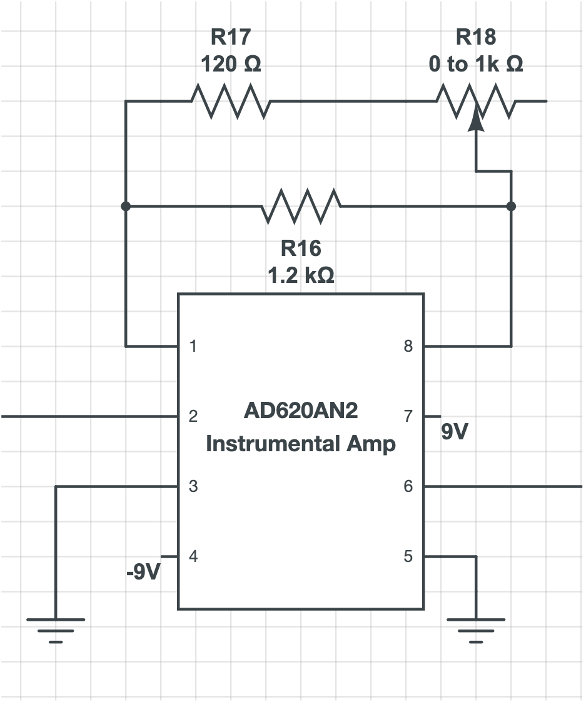
- Instrumental Amplifier (gain ~91)
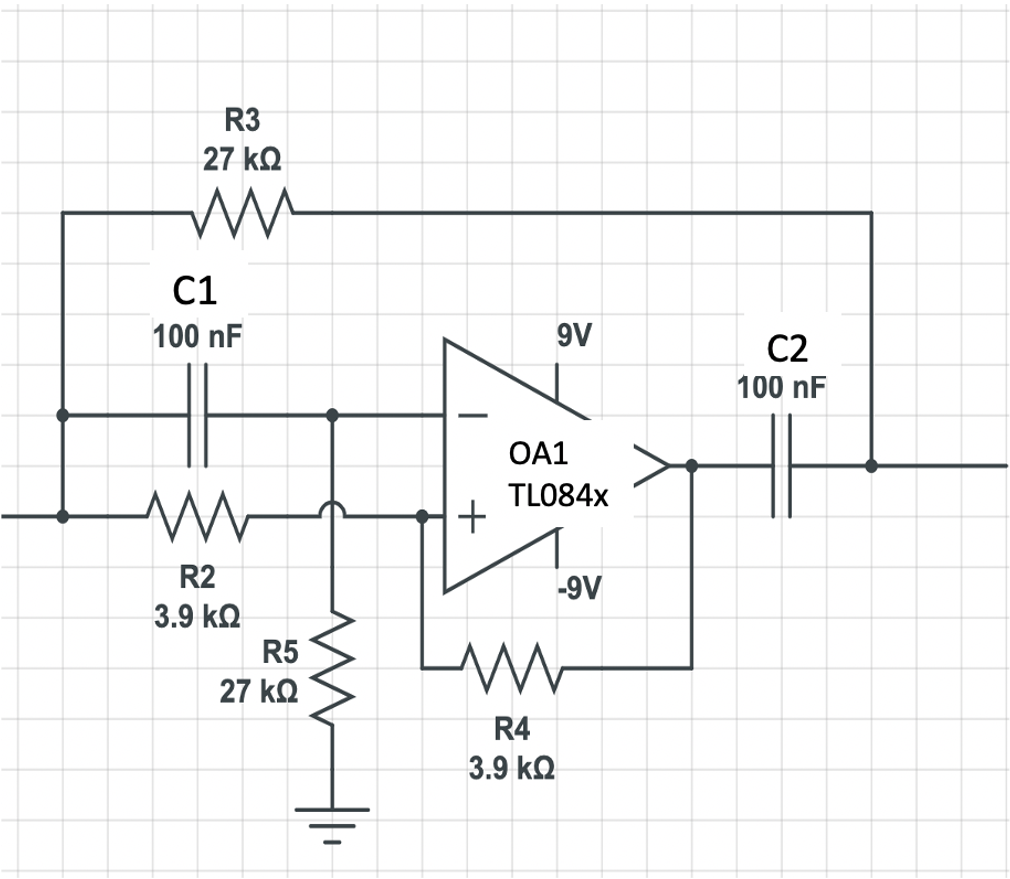
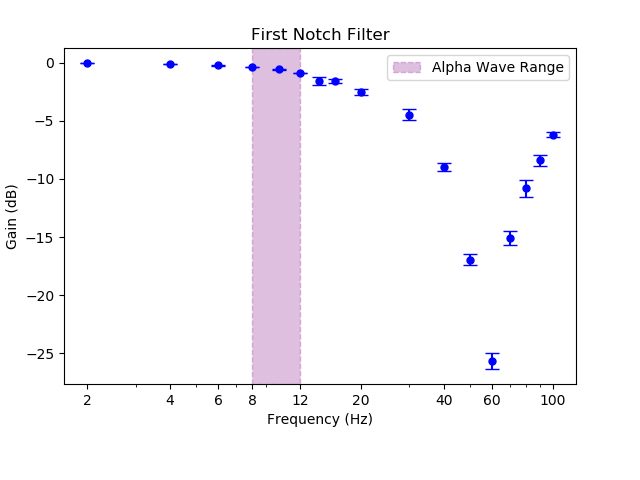
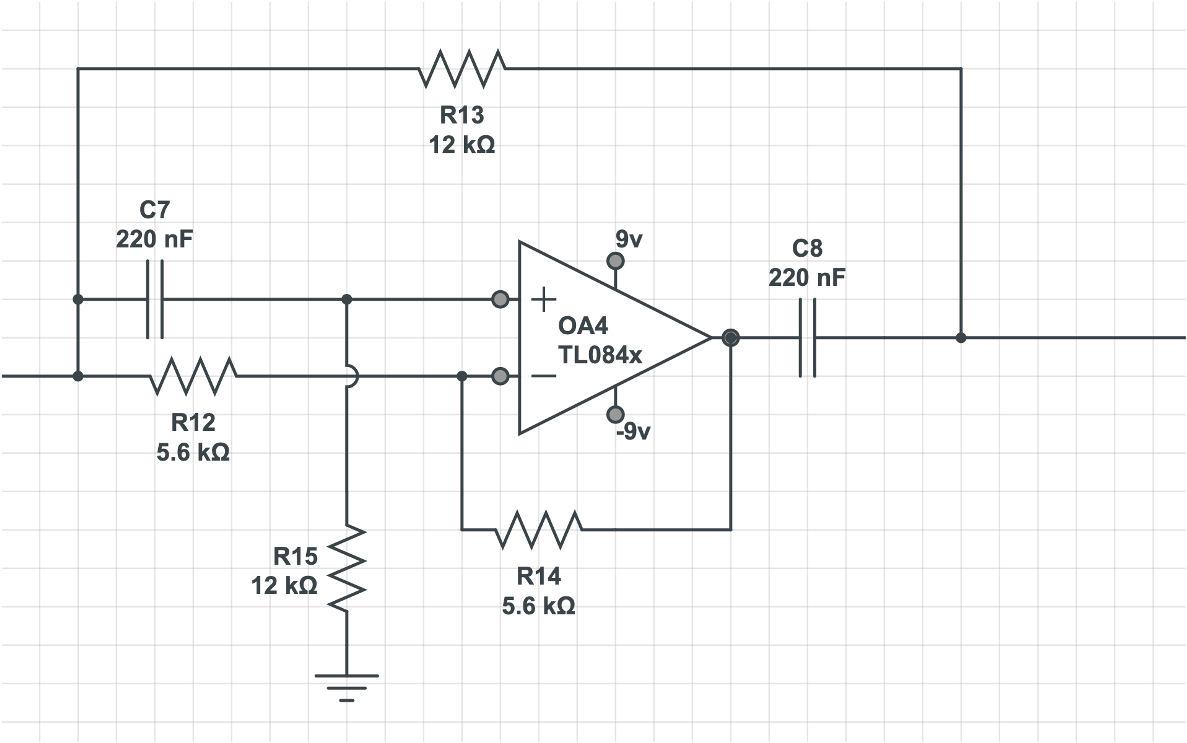
- Notch Filter (60 HZ, gain = 1)
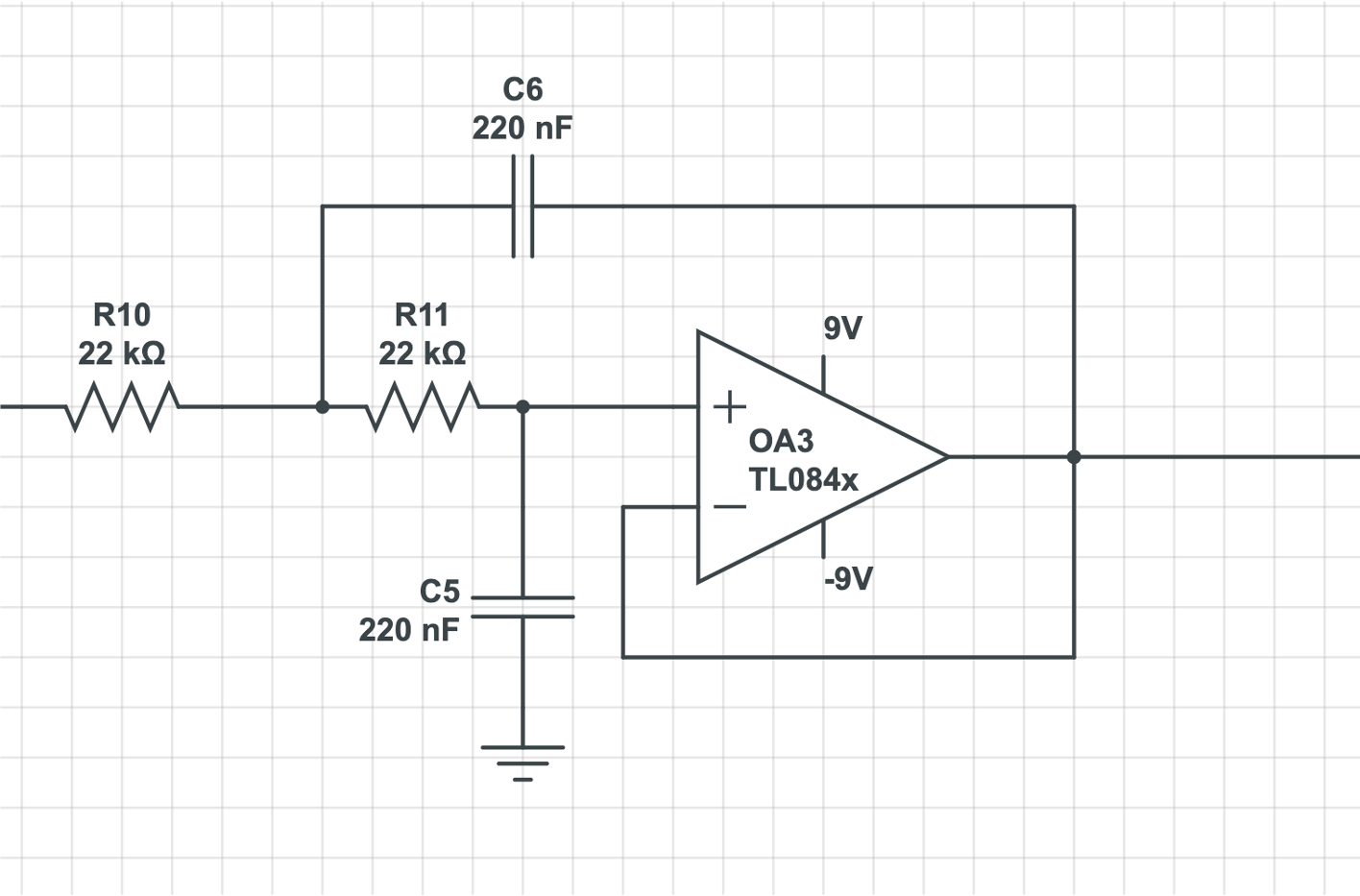
- High Pass Filter (Fc = 7.2 Hz, gain = 1)
- Low Pass Filter (Fc = 32.9 Hz, gain = 1)
- Instrumental Amplifier with variable gain (gain ~ 90-460)
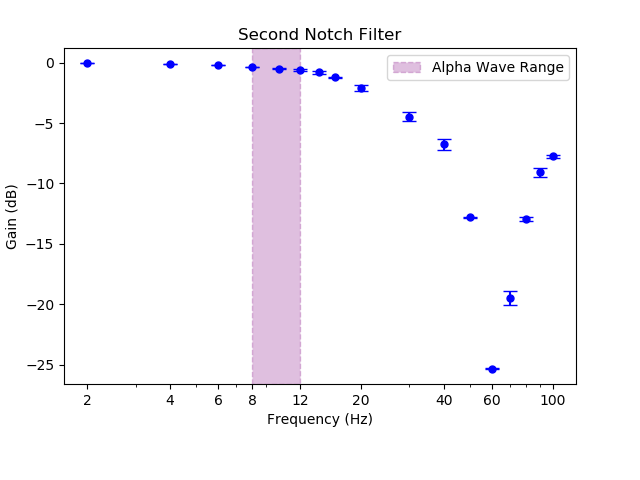
- Notch Filter (60 HZ, gain = 1)
Individual Section are discussed further below.
Alpha wave signals is 15-50 uV so we need a lot of amplification in the circuit. (LETS CITE INFORMATION) An instrumentation amplifier takes as its inputs, 2 voltages, and outputs the difference between the two multiplied by some gain given by: G = 1 + (50.5 kOhm)/R, where R is the total resistance between pin 1 and 8. Note it is possible to make home-made instrumentation amplifier usually with 3 op-amps. However, it suffers from a low CMRR unless precision resitors are used. (CITE DIY)The biggest source of noise in our system is centered at 60 Hz due to power line interference. This noise is present even though we use batteries to power the circuit. Thus we have 2 notch filters in the circuit (filters that have a severe reduction of gain around 1 particular frequency). The first notch filter intends to filter out interference before more gains are applied.
The notch frequency is given by f = 1/(2 PI R C) where R = R3 = R5. The other two resistor values are related to the quality factor of the filter, which determines how sharp the attenuation is.
The high pass filter intends to filter out frequencies corresponding to galvanic skin response across our head. This interference is primarily low frequency. A second order active filter design is used here and is shown to be necessary for noise reduction.
The EEG waves of interest to our project are alpha (8-12 HZ) and beta waves (12-30 HZ). Thus, we are not interested in frequency > 30HZ and filter them out. A second order filter design is used.
This 90-460 gain is on top of the 90x gain from the first instrumentation amplifier. Alpha wave amplitude varies from person to person, from about 10 to 30 uV. Using a middle value of 20 uV, this means the ending voltage reading could range from 909020e-6 = 0.162V to 4609020e-6 = 0.828V. The variable gain is achieved by putting resitors in series and in parallel. The gain is roughly in the range of 90-460, which corresponds to potentiometer value 1k (maximum) to 0 (minimum).
To adjust the potentiometer, start taking readings and make sure one is not moving at all. Make sure voltages don't fluctuate offscreen, but avoid making it too small because then the errors incurred from digitally reading the data into rpi would be relatively increased.
Another 60 HZ is necessary at the end of the circuit since the power line interferences seep into the circuit through prior steps. This is the exact copy of the 1st notch filter
Supply the ADC chip with 5V from Rpi to ensure the maximum input voltage range possible. The pin configuration and connection in the image above is correct, but it is reccomended to double check the connection, because wiring mistakes can lead to damaging the chip and or the Rpi.
[Gaussian_eval.py](link later)
This code is created to 1) find the optimal voltage threshold which separates relaxed and concentrated data and 2) Evaluate how distinct the relaxed and concentrated datasets using statistical analysis.
We approximate concentrated and relaxed brain wave data sets each as normal Gaussian distributions. The cross point of the two gaussians give the best threshold voltage V0 which separates relaxed and concentrated data. This voltage threhold would minimizes overall wrong classifications. The overlap area divided by 2 give the probability of wrong classification since we have two normal distributions. More specifically, the ratio of overlap area left of V0 to right of V0 gives the percentage of wrong estimation being we guessed concentrated but is actually relaxed.
(EXPLAIN DB AND TALK ABOUT THE NECESSARY LEVEL OF NOISE ATTENUATION TO SEE BRAIN WAVE DATA)We built our circuit to measure Alpha waves which are from 8-12Hz. When relaxed the power of these waves should increase and when concentrating the power of these waves should decrease. To test relaxed state the user closes their eyes, to test concentrating the user opens their eyes and look at 'crazy' images.
| Relaxed | Concentrating |
|---|---|
| 689 | 85 |
| 958 | 531 |
| 829 | 429 |
| 802 | 50 |
| 421 | 112 |
| Relaxed | Concentrating |
|---|---|
| 5,294 | 23,384 |
| 4,848 | 36,822 |
| 5,077 | 39, 640 |
| 11,051 | 55,365 |
| 5,748 | 32,897 |
- Accurate positioning of electrodes plays an fundamental role in good EEG data acquisition. needs to be pin-pointed and quite exact
The circuit has already shown success in filtering out noise in a wide frequency range (caused by skin, power line, etc). However, it is still subject to artefact signals unrelated to the brain waves of interest. The method we would like to experiment in the future is independent component analysis (ICA). It has shown to be a robust method used for EEG in field as well as in research to separate mixture of brain activities, as well as to eliminate contamination of signals by eye movements, blinks, muscle, heart and line noise.
ICA is a signal processing method to separate independent sources linearly mixed in several sensors. ICA recovers a version of the original sources, by multiplying the data with an unmixing matrix: U = WX, where X is the data with dimension (channel * time), U is the ICA source activties (components * time), and W is the ICA unmixing matrix. ICA separates out the independent components by finding W such to minimize the gaussianicity of each data set.
To apply ICA to EEG data, we assume the following
- Mixing is linear at electrodes
- Propagation Delays are negligible
- Component time courses are independent
- Number of components are equal or less than the number of channels
- Meditation Score App based on Alpha Wave
- Child Concentration Monitor
- The project owes much thanks to instructables.com/DIY-EEG-and-ECG-Circuit/. We have based our procedures and methods on the instructions in this article, but we created our own circuit design and wrote our own code for data-taking and analysis.
- EEG and Alpha Wave informtions are largely from Wikipedia.
- Independent Component Analysis: http://arnauddelorme.com/ica_for_dummies/; youtube series https://www.youtube.com/watch?v=kWAjhXr7pT4&list=PLXc9qfVbMMN2uDadxZ_OEsHjzcRtlLNxc&index=2; https://sccn.ucsd.edu/~jung/Site/EEG_artifact_removal.html
- Flappy bird code reference: https://github.com/clear-code-projects/FlappyBird_Python