/mst

Minimum spanning trees of random, complete, undirected graphs

Primary LanguageJavaMIT LicenseMIT

MST

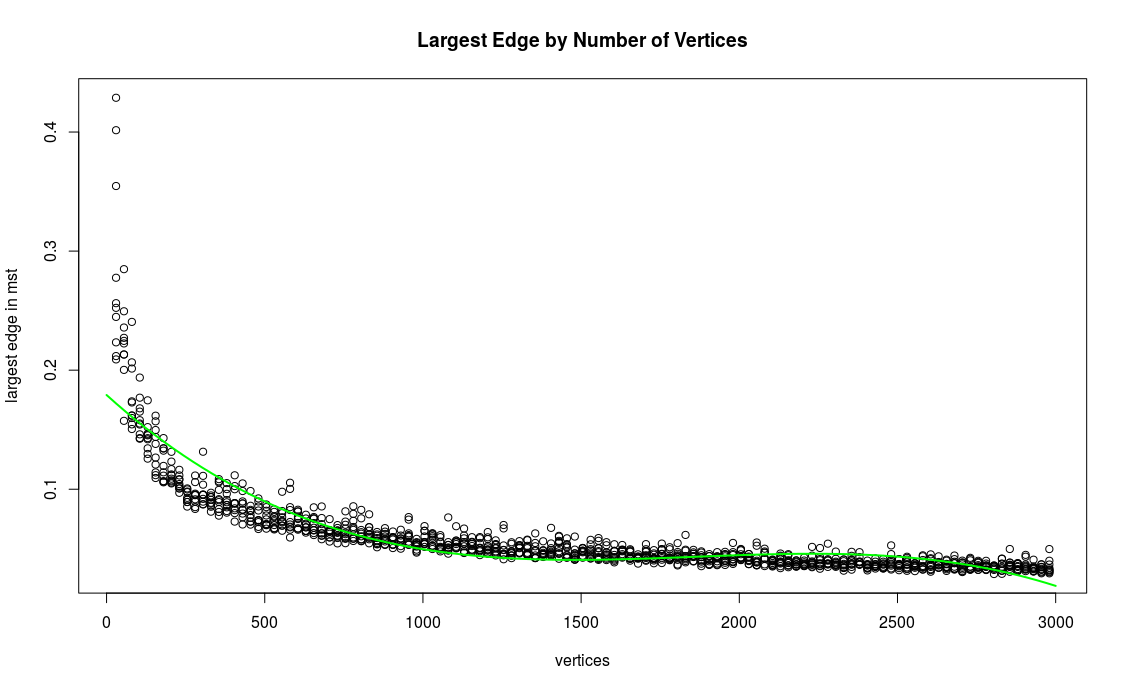
Finding the MST of a complete graph

Why find a function to reduce edges

The most computationally intensive step of the program is the instantiation and storage of edges. At a point the JVM will be unable to allocate enough memory for a large enough set of vertices.

There is insufficient memory for the Java Runtime Environment to continue.
Native memory allocation (mmap) failed to map 1096810496 bytes for committing reserved memory.

Largest Edge by Number of Vertices

Third degree polynomial fit

Call:
lm(formula = y ~ poly(x, 3, raw = TRUE), data = d)

Residuals:
      Min        1Q    Median        3Q       Max
-0.040845 -0.007238 -0.000260  0.005428  0.256759

Coefficients:
                          Estimate Std. Error t value Pr(>|t|)    
(Intercept)              1.791e-01  2.170e-03   82.56   <2e-16 ***
poly(x, 3, raw = TRUE)1 -2.401e-04  6.206e-06  -38.70   <2e-16 ***
poly(x, 3, raw = TRUE)2  1.349e-07  4.776e-09   28.24   <2e-16 ***
poly(x, 3, raw = TRUE)3 -2.421e-11  1.043e-12  -23.20   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0179 on 1186 degrees of freedom
Multiple R-squared:  0.7798,	Adjusted R-squared:  0.7793
F-statistic:  1400 on 3 and 1186 DF,  p-value: < 2.2e-16

alt text