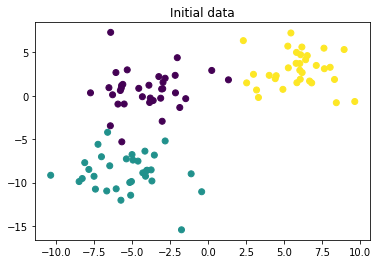
Реализуйте алгоритм к ближайших соседей. Создадим искуственный набор данных из 100 наблюдений с 3 классами. Необходимо реализовать функцию на входе которой:
- тренировочный набор данных (признаки и метки классов);
- тестовый набор данных (признаки);
-
$k$ - количество ближайших соседей.
На выходе функция должна возвращать метки тестового набора данных. В качестве расстояния между объектами следует использовать Эвклидову меру.
Алгоритм к ближайших соседей:
Для каждого объекта тестового набора данных:
- вычисление расстояний между всеми объектами тренировочного набора;
- определение
$k$ наименьших расстояний; - определение классов для
$k$ найденных объектов; - присваивание метки тестовому объекту класса, который превалирует среди найденных объектов.
В многоклассовой модели может возникнуть неопределенность, что в 3 найденных объектак будут присутсвовать разные классы. В этом случае необходимо присваивать класс случайным образом.
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
import math
import random
import numpy as npX, Y = make_blobs(n_samples = 100, n_features=2, centers=3, cluster_std = 2, random_state=17)plt.scatter(X[:,0], X[:,1], c=Y)
plt.title('Initial data')Text(0.5,1,'Initial data')
def get_distance(first_point, second_point):
square_sum = 0
for dimension in range(len(first_point)):
square_sum = square_sum + (first_point[dimension] - second_point[dimension]) ** 2
return math.sqrt(square_sum);def calculate_distances(x_train, point):
distances = []
for index, train_point in enumerate(x_train):
distances.append([index, get_distance(point, train_point)])
distances.sort(key = lambda x: x[1])
return distances;def get_nearest_neighbours_indexes_for_point(x_train, point, k):
distances = calculate_distances(x_train, point)
return list(map(lambda p: p[0], distances[:k]))def get_appropriate_category(categories):
counts = {}
for cat in categories:
if (cat in counts):
counts[cat] = counts[cat] + 1
else:
counts[cat] = 1
keys_list = list(counts.keys())
values_list = list(counts.values())
max_count = max(values_list)
maximums = []
for cat in keys_list:
if counts[cat] == max_count:
maximums.append(cat);
return random.choice(maximums)def funct_kNN(x_train, y_train, x_test, k):
y_test = []
for test_point in x_test:
neighbours_indeces = get_nearest_neighbours_indexes_for_point(x_train, test_point, k)
neighbours_categories = list(map(lambda index: y_train[index], neighbours_indeces))
appropriate_category = get_appropriate_category(neighbours_categories)
y_test.append(appropriate_category);
return np.array(y_test)Для корректного анализа построенного классификатора, разбейте исходный набор данных на тренировочный и тестовый.
Проверьте качество классификации для различных параметров
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
def calculate_accuracy(k):
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.5, random_state=42)
y_pred = funct_kNN(x_train, y_train, x_test, k)
accuracy = accuracy_score(y_test, y_pred)
return accuracy
for k in (1, 3, 5, 7, 9):
print('Для', k, 'соседей вероятность попадания равна', calculate_accuracy(k))Для 1 соседей вероятность попадания равна 0.94
Для 3 соседей вероятность попадания равна 0.98
Для 5 соседей вероятность попадания равна 0.98
Для 7 соседей вероятность попадания равна 0.96
Для 9 соседей вероятность попадания равна 0.96
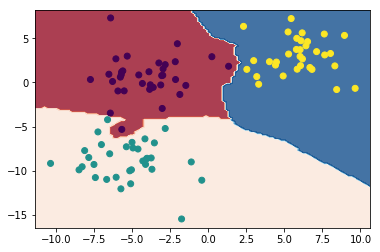
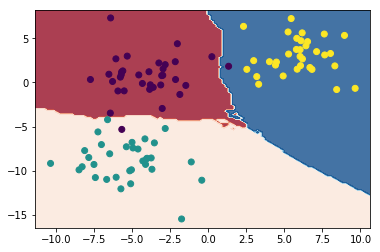
Постройте разделающие поверхности, которые строит классификатор
def print_decision_surace(k):
h = 0.2
x0_min, x0_max = np.min(X[:,0]) - 1, np.max(X[:,0]) + 1
x1_min, x1_max = np.min(X[:,1]) - 1, np.max(X[:,1]) + 1
xx0, xx1 = np.meshgrid(np.arange(x0_min, x0_max, h), np.arange(x1_min, x1_max, h))
z = funct_kNN(X, Y, np.stack((xx0.ravel(),xx1.ravel())).transpose(), k).reshape(xx0.shape)
plt.contourf(xx0, xx1, z, cmap=plt.cm.RdBu, alpha=.8)
plt.scatter(X[:,0], X[:,1], c = Y)
plt.show()for k in (1, 3, 5, 7, 9):
print('Для', k, 'соседей')
print_decision_surace(k)Для 1 соседей
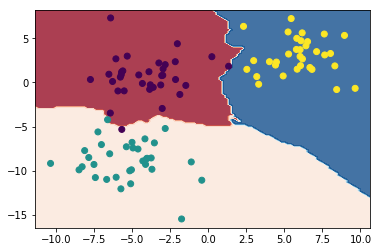
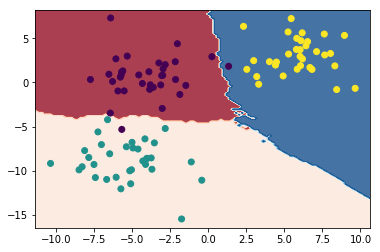
Для 3 соседей
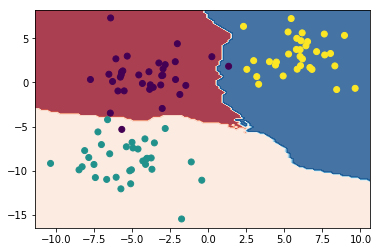
Для 5 соседей
Для 7 соседей
Для 9 соседей
Напишите функцию для регрессии методом к ближайших соседей.
Для проверки вашего регрессионной модели создайте функцию синуса в диапазоне [0, 5] и возьмите в этом диапазоне 10 случайных точек как тренеровочную выборку.
Задача: предсказать функцию на всем диапазоне [0, 5] для всех возможных значений параметра
Алгоритм регрессии:
Для каждого тестового обекта:
- вычисление расстояний между всеми тренировочными объектами (можно использовать просто разницу по модулю между признаками объектов, так как у нас всего один признак в задаче);
- нахождение
$k$ объектов с минимальными расстояниями; - вычисление среднего значения по к найденным объектам и присваивание этого значения тестовому объекту.
values = []
sinuses = []
value_min = 0
value_max = 5
values_count = 10
for index in range(values_count):
value = random.uniform(value_min, value_max)
sinus = math.sin(value)
values.append(value)
sinuses.append(sinus)
def get_appropriate_value(values, sinuses, value, k):
nearest_indexes = get_nearest_neighbours_indexes_for_point(list(map(lambda val: [val], values)), [value], k)
sinuses_sum = 0
for index in nearest_indexes:
sinuses_sum += sinuses[index]
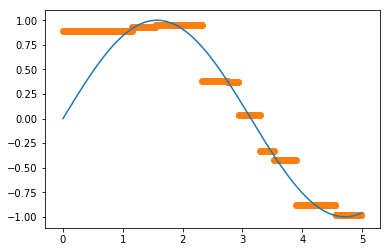
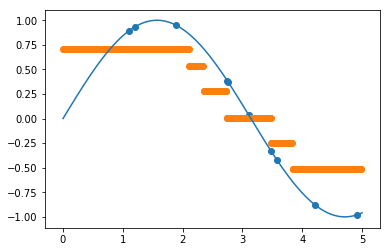
return sinuses_sum / kПостройте на одном графике исходную функцию, тренировочные объекты и предсказанные функции для каждого значения
def show_result(k):
pred_values = np.arange(value_min, value_max, 0.01)
pred_sinuses = list(map(lambda val: get_appropriate_value(values, sinuses, val, k), pred_values))
xpts = np.linspace(value_min, value_max, 500)
test_v = np.vectorize(lambda val: math.sin(val))
plt.plot(xpts, test_v(xpts))
plt.scatter(values, sinuses)
plt.scatter(pred_values, pred_sinuses)
plt.show()
for k in (1, 3, 5, 7, 9):
print('Для', k, 'соседей')
show_result(k)Для 1 соседей
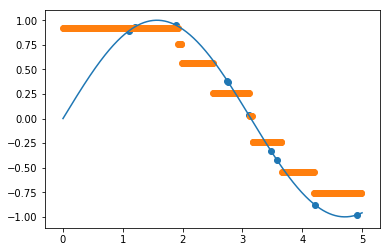
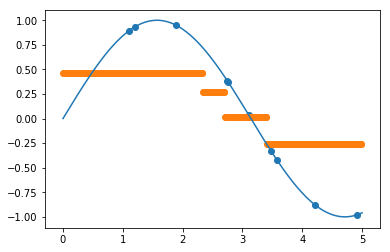
Для 3 соседей
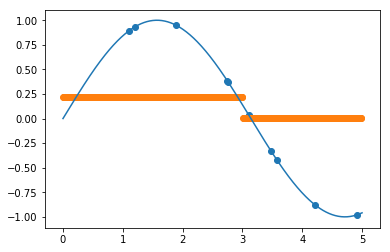
Для 5 соседей
Для 7 соседей
Для 9 соседей