S + Autograd + XLA
Autograd and XLA for S-parameters - a scatter parameter circuit simulator and optimizer for the frequency domain based on JAX.
The simulator was developed for simulating Photonic Integrated Circuits but in fact is able to perform any S-parameter based circuit simulation. The goal of SAX is to be a thin wrapper around JAX with some basic tools for S-parameter based circuit simulation and optimization. Therefore, SAX does not define any special datastructures and tries to stay as close as possible to the functional nature of JAX. This makes it very easy to get started with SAX as you only need functions and standard python dictionaries. Let's dive in...
Full Quick Start page - Documentation.
Let's first import the SAX library, along with JAX and the JAX-version of numpy:
import sax
import jax
import jax.numpy as jnpDefine a model function for your component. A SAX model is just a function that returns an 'S-dictionary'. For example a directional coupler:
def coupler(coupling=0.5):
kappa = coupling**0.5
tau = (1-coupling)**0.5
sdict = sax.reciprocal({
("in0", "out0"): tau,
("in0", "out1"): 1j*kappa,
("in1", "out0"): 1j*kappa,
("in1", "out1"): tau,
})
return sdict
coupler(coupling=0.3){('in0', 'out0'): 0.8366600265340756,
('in0', 'out1'): 0.5477225575051661j,
('in1', 'out0'): 0.5477225575051661j,
('in1', 'out1'): 0.8366600265340756,
('out0', 'in0'): 0.8366600265340756,
('out1', 'in0'): 0.5477225575051661j,
('out0', 'in1'): 0.5477225575051661j,
('out1', 'in1'): 0.8366600265340756}
Or a waveguide:
def waveguide(wl=1.55, wl0=1.55, neff=2.34, ng=3.4, length=10.0, loss=0.0):
dwl = wl - wl0
dneff_dwl = (ng - neff) / wl0
neff = neff - dwl * dneff_dwl
phase = 2 * jnp.pi * neff * length / wl
amplitude = jnp.asarray(10 ** (-loss * length / 20), dtype=complex)
transmission = amplitude * jnp.exp(1j * phase)
sdict = sax.reciprocal({("in0", "out0"): transmission})
return sdict
waveguide(length=100.0){('in0', 'out0'): 0.97953-0.2013j, ('out0', 'in0'): 0.97953-0.2013j}
These component models can then be combined into a circuit:
mzi, _ = sax.circuit(
netlist={
"instances": {
"lft": coupler,
"top": waveguide,
"rgt": coupler,
},
"connections": {
"lft,out0": "rgt,in0",
"lft,out1": "top,in0",
"top,out0": "rgt,in1",
},
"ports": {
"in0": "lft,in0",
"in1": "lft,in1",
"out0": "rgt,out0",
"out1": "rgt,out1",
},
}
)
type(mzi)function
As you can see, the mzi we just created is just another component model function! To simulate it, call the mzi function with the (possibly nested) settings of its subcomponents. Global settings can be added to the 'root' of the circuit call and will be distributed over all subcomponents which have a parameter with the same name (e.g. 'wl'):
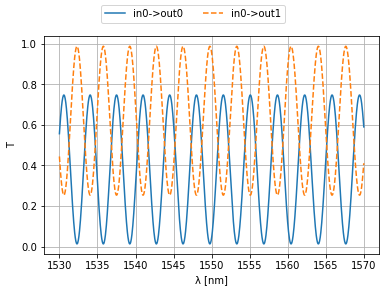
wl = jnp.linspace(1.53, 1.57, 1000)
result = mzi(wl=wl, lft={'coupling': 0.3}, top={'length': 200.0}, rgt={'coupling': 0.8})
plt.plot(1e3*wl, jnp.abs(result['in0', 'out0'])**2, label="in0->out0")
plt.plot(1e3*wl, jnp.abs(result['in0', 'out1'])**2, label="in0->out1", ls="--")
plt.xlabel("λ [nm]")
plt.ylabel("T")
plt.grid(True)
plt.figlegend(ncol=2, loc="upper center")
plt.show()Those are the basics. For more info, check out the full SAX Quick Start page or the rest of the Documentation.
You can install SAX with pip:
pip install saxIf you want to be able to run all the example notebooks, you'll need python>=3.10 and you should install the development version of SAX:
pip install 'sax[dev]'Copyright © 2023, Floris Laporte, Apache-2.0 License