stock copula

任务

第一步

将收益率进行对数化处理得到收益率序列，对收益率序列进行JB检验，ADF检验和ARCH-LM(10)检验

第二步

对各收益率序列先建立ARMA模型拟合序列的条件均值（按照 AIC准则选择最佳的ARMA模型进行拟合）

第三步

用GARCH(1,1)拟合收益率的残差序列，并对GARCH的残差进行ADF，BDS检验和CvM检验

第四步

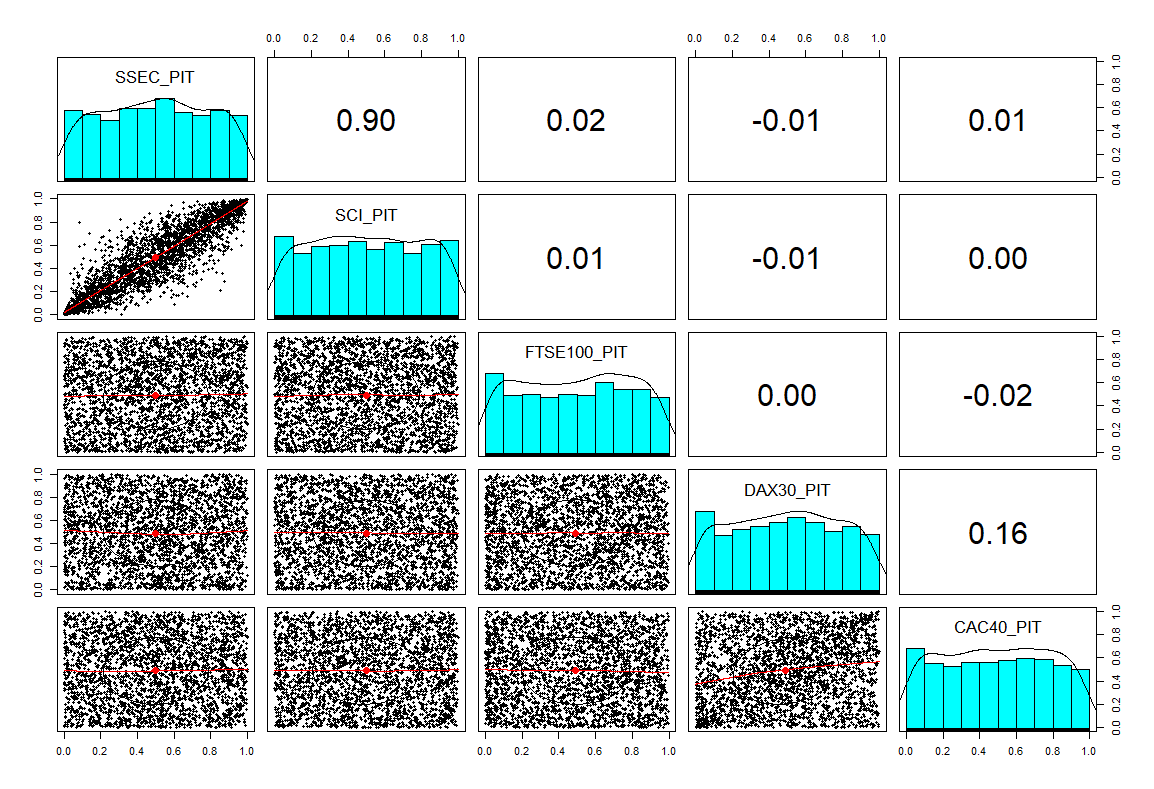
对残差序列进行标准化处理再进行概率积分变换（假设为t分布）。然后计算任意两国股指序列间的Kendall系数，得到配对图

第六步

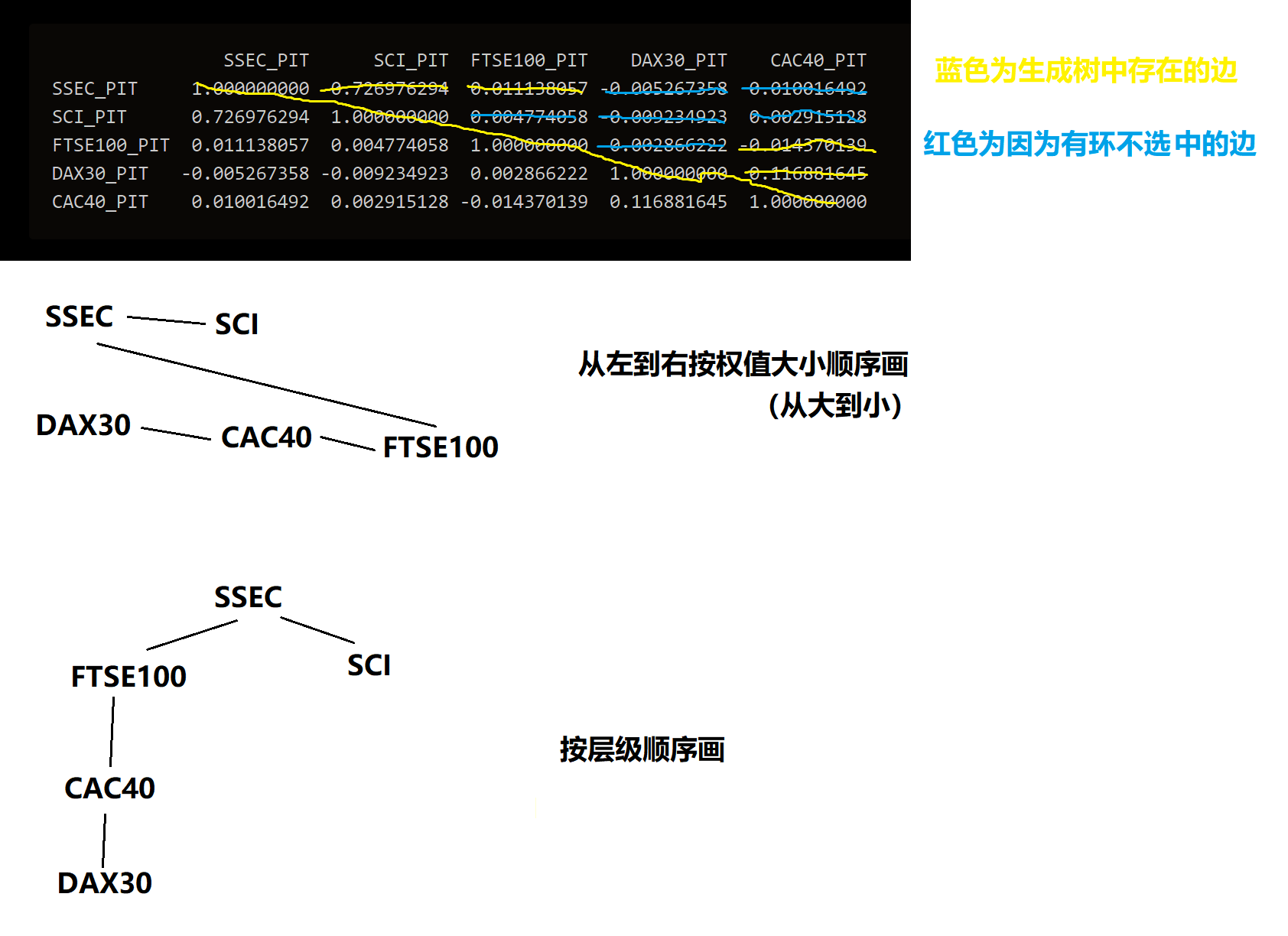
构建Copula树：每个节点是一个股指收益率序列，根据极大似然估计及AIC准则确定树中每条边对应的Copula函数类型。以第四步计算的相关性作为边权值，建立最大生成树

第八步

评价最大生成树中每条边（对应一个Copula模型）的拟合结果（用AIC、BIC和loss值三个指标）

第一步

对收益率

SSEC

JB检验： Jarque_beraResult(statistic=5922.418016821695, pvalue=0.0)
ADF检验： (-9.840797680673846, 4.7594468861661446e-17, 27, 2889, {'1%': -3.432615531267606, '5%': -2.8625409589326205, '10%': -2.5673028391515254}, -21733.928302635803)
ARCH效应检验：Chi-squared = 380.56, df = 10, p-value < 2.2e-16

SCI

JB检验： Jarque_beraResult(statistic=1922.9291939615061, pvalue=0.0)
ADF检验： (-14.2597311275576, 1.4334971007230296e-26, 13, 2903, {'1%': -3.4326045958386953, '5%': -2.862536129260207, '10%': -2.567300267867621}, -20574.45350851521)
ARCH效应检验：Chi-squared = 357.91, df = 10, p-value < 2.2e-16

FTSE100

JB检验： Jarque_beraResult(statistic=13094.463375384035, pvalue=0.0)
ADF检验： (-16.826211955918293, 1.167669855767656e-29, 12, 3017, {'1%': -3.4325193312999036, '5%': -2.8624984712561274, '10%': -2.567280219110819}, -23969.535430552045)
ARCH效应检验：Chi-squared = 698.07, df = 10, p-value < 2.2e-16

DAX30

JB检验： Jarque_beraResult(statistic=7339.559305081821, pvalue=0.0)
ADF检验： (-16.327113802190908, 3.08674593815361e-29, 10, 3033, {'1%': -3.4325078777082796, '5%': -2.8624934125717725, '10%': -2.567277525930013}, -22658.135809125994)
ARCH效应检验：Chi-squared = 552.41, df = 10, p-value < 2.2e-16

CAC40

JB检验： Jarque_beraResult(statistic=8109.087761470604, pvalue=0.0)
ADF检验： (-20.10586187025487, 0.0, 7, 3065, {'1%': -3.432485329568554, '5%': -2.8624834537243493, '10%': -2.5672722239727066}, -22955.17483627421)
ARCH效应检验：Chi-squared = 542.23, df = 10, p-value < 2.2e-16

第二步

ARIMA最优模型

SSEC

ARIMA(5,0,3) with zero mean 

Coefficients:
         ar1     ar2     ar3     ar4      ar5      ma1     ma2      ma3
      0.2987  -0.952  0.1237  0.0157  -0.0173  -0.2660  0.9336  -0.0781
s.e.  0.7602   0.158  0.7119  0.0465   0.0267   0.7602  0.1328   0.7043

sigma^2 = 3.146e-05:  log likelihood = 10984.84
AIC=-21951.67   AICc=-21951.61   BIC=-21897.87

SCI

ARIMA(1,0,1) with zero mean 

Coefficients:
          ar1     ma1
      -0.8882  0.9166
s.e.   0.0421  0.0364

sigma^2 = 4.716e-05:  log likelihood = 10391.47
AIC=-20776.95   AICc=-20776.94   BIC=-20759.01

FTSE100

ARIMA(5,0,5) with zero mean 

Coefficients:
          ar1     ar2      ar3     ar4     ar5     ma1      ma2     ma3
      -0.1726  0.2969  -0.3699  0.3401  0.7752  0.1639  -0.3170  0.3652
s.e.   0.0850  0.0714   0.1144  0.0638  0.0748  0.0814   0.0646  0.1123
          ma4      ma5
      -0.3882  -0.7517
s.e.   0.0619   0.0880

sigma^2 = 1.966e-05:  log likelihood = 12123.78
AIC=-24225.56   AICc=-24225.47   BIC=-24159.38

DAX30

ARIMA(0,0,0) with zero mean 

sigma^2 = 3.161e-05:  log likelihood = 11452.01
AIC=-22902.01   AICc=-22902.01   BIC=-22895.99

CAC40

ARIMA(0,0,0) with zero mean 

sigma^2 = 3.081e-05:  log likelihood = 11600.13
AIC=-23198.25   AICc=-23198.25   BIC=-23192.22

第三步

用GARCH拟合ARIMA最优模型的残差

SSEC

GARCH

        Estimate  Std. Error  t value Pr(>|t|)    
mu     1.269e-04   7.230e-05    1.755  0.07920 .  
omega  2.527e-07   8.340e-08    3.030  0.00245 ** 
alpha1 5.609e-02   8.540e-03    6.567 5.12e-11 ***
beta1  9.378e-01   8.659e-03  108.308  < 2e-16 ***
shape  4.580e+00   4.070e-01   11.255  < 2e-16 ***

ADF检验：Dickey-Fuller = -13.721, Lag order = 14, p-value = 0.01（实际比这个小）
BDS检验

Epsilon for close points =  0.0028 0.0056 0.0084 0.0112 

Standard Normal = 
      [ 0.0028 ] [ 0.0056 ] [ 0.0084 ] [ 0.0112 ]
[ 2 ]     4.9865     7.0757     9.0644    10.4787
[ 3 ]     7.2637     9.9598    12.0665    13.7297

p-value = 
      [ 0.0028 ] [ 0.0056 ] [ 0.0084 ] [ 0.0112 ]
[ 2 ]          0          0          0          0
[ 3 ]          0          0          0          0

CVM检验：omega2 = 962.98, p-value < 2.2e-16

SCI

GARCH

        Estimate  Std. Error  t value Pr(>|t|)    
mu     1.385e-04   9.827e-05    1.409  0.15883    
omega  5.991e-07   1.867e-07    3.208  0.00133 ** 
alpha1 5.881e-02   8.714e-03    6.749 1.49e-11 ***
beta1  9.292e-01   1.004e-02   92.556  < 2e-16 ***
shape  5.683e+00   6.067e-01    9.366  < 2e-16 ***

ADF检验：Dickey-Fuller = -13.723, Lag order = 14, p-value = 0.01（实际比这个小）
BDS检验

Epsilon for close points =  0.0034 0.0069 0.0103 0.0137 

Standard Normal = 
      [ 0.0034 ] [ 0.0069 ] [ 0.0103 ] [ 0.0137 ]
[ 2 ]     4.0122     5.6464     7.7869     9.8539
[ 3 ]     6.4152     8.3825    10.9933    13.2679

p-value = 
      [ 0.0034 ] [ 0.0069 ] [ 0.0103 ] [ 0.0137 ]
[ 2 ]      1e-04          0          0          0
[ 3 ]      0e+00          0          0          0

CVM检验：omega2 = 960.45, p-value < 2.2e-16

FTSE100

GARCH

Coefficient(s):
        Estimate  Std. Error  t value Pr(>|t|)    
mu     2.744e-04   5.851e-05    4.690 2.74e-06 ***
omega  6.905e-07   1.672e-07    4.129 3.64e-05 ***
alpha1 1.370e-01   2.068e-02    6.622 3.56e-11 ***
beta1  8.305e-01   2.431e-02   34.161  < 2e-16 ***
shape  6.059e+00   6.654e-01    9.105  < 2e-16 ***

ADF检验：Dickey-Fuller = -13.919, Lag order = 14, p-value = 0.01（实际比这个小）
BDS检验

Epsilon for close points =  0.0022 0.0044 0.0066 0.0089 

Standard Normal = 
      [ 0.0022 ] [ 0.0044 ] [ 0.0066 ] [ 0.0089 ]
[ 2 ]    12.0353    12.6627    12.8609    13.2519
[ 3 ]    16.0576    16.4353    16.3417    16.5075

p-value = 
      [ 0.0022 ] [ 0.0044 ] [ 0.0066 ] [ 0.0089 ]
[ 2 ]          0          0          0          0
[ 3 ]          0          0          0          0

CVM检验：omega2 = 1005, p-value < 2.2e-16

DAX30

GARCH

        Estimate  Std. Error  t value Pr(>|t|)    
mu     3.512e-04   7.154e-05    4.909 9.17e-07 ***
omega  5.466e-07   1.692e-07    3.230  0.00124 ** 
alpha1 1.147e-01   1.819e-02    6.303 2.92e-10 ***
beta1  8.777e-01   1.813e-02   48.398  < 2e-16 ***
shape  4.999e+00   4.935e-01   10.129  < 2e-16 ***

ADF检验：Dickey-Fuller = -14.072, Lag order = 14, p-value = 0.01（实际比这个小）
BDS检验

Epsilon for close points =  0.0028 0.0056 0.0084 0.0112 

Standard Normal = 
      [ 0.0028 ] [ 0.0056 ] [ 0.0084 ] [ 0.0112 ]
[ 2 ]    10.0683     9.4842     9.8153     9.2503
[ 3 ]    14.4560    13.5235    13.6332    13.3037

p-value = 
      [ 0.0028 ] [ 0.0056 ] [ 0.0084 ] [ 0.0112 ]
[ 2 ]          0          0          0          0
[ 3 ]          0          0          0          0

CVM检验：omega2 = 1014.8, p-value < 2.2e-16

CAC40

GARCH

        Estimate  Std. Error  t value Pr(>|t|)    
mu     3.409e-04   6.835e-05    4.987 6.12e-07 ***
omega  6.014e-07   1.647e-07    3.652 0.000261 ***
alpha1 1.372e-01   2.021e-02    6.791 1.11e-11 ***
beta1  8.548e-01   1.933e-02   44.210  < 2e-16 ***
shape  5.192e+00   4.897e-01   10.604  < 2e-16 ***

ADF检验：Dickey-Fuller = -14.861, Lag order = 14, p-value = 0.01（实际比这个小）
BDS检验

Epsilon for close points =  0.0028 0.0056 0.0083 0.0111 

Standard Normal = 
      [ 0.0028 ] [ 0.0056 ] [ 0.0083 ] [ 0.0111 ]
[ 2 ]    12.7196    11.4585    11.0073    10.0493
[ 3 ]    18.3638    16.3068    15.1014    13.9452

p-value = 
      [ 0.0028 ] [ 0.0056 ] [ 0.0083 ] [ 0.0111 ]
[ 2 ]          0          0          0          0
[ 3 ]          0          0          0          0

CVM检验：omega2 = 1014.6, p-value < 2.2e-16

第四步

Kendall相关度

                SSEC_PIT      SCI_PIT  FTSE100_PIT    DAX30_PIT    CAC40_PIT
SSEC_PIT     1.000000000  0.726898701  0.010906220 -0.005301217  0.009875415
SCI_PIT      0.726898701  1.000000000  0.005022354 -0.009410330  0.002810261
FTSE100_PIT  0.010906220  0.005022354  1.000000000  0.002791451 -0.014208841
DAX30_PIT   -0.005301217 -0.009410330  0.002791451  1.000000000  0.114052574
CAC40_PIT    0.009875415  0.002810261 -0.014208841  0.114052574  1.000000000

配对图

第六步

最大生成树的边参数

SSEC-SCI: family = t, rotation = 0, parameters = 0.99, 4.97（边权值0.726976294）
DAX30-CAC40: family = bb1, rotation = 180, parameters = 0, 6.56（边权值0.116881645）
FTSE100-CAC40: family = t, rotation = 0, parameters = 0.97, 5.07（边权值-0.014370139）
SSEC-FTSE100: family = t, rotation = 0, parameters = 0.97, 5.07（边权值0.011138057）

最大生成树结构

第八步

上一步建立的copula模型指标：

SSEC-SCI：AIC -9105.955 BIC -9093.998
DAX30-CAC40: AIC -5490.886 BIC -5478.929
FTSE100-CAC40：AIC -5622.067 BIC -5610.11
SSEC-FTSE100: AIC -4696.484 BIC -4684.528

以上模型负对数似然都是收敛到负无穷

sg-first/stock-copula

stock copula

任务

第一步

第二步

第三步

第四步

第六步

第八步

第一步

SSEC

SCI

FTSE100

DAX30

CAC40

第二步

SSEC

SCI

FTSE100

DAX30

CAC40

第三步

SSEC

SCI

FTSE100

DAX30

CAC40

第四步

Kendall相关度

配对图

第六步

最大生成树的边参数

最大生成树结构

第八步