Knight's Tour Visualization

An online Knight's tour visualizer using divide and conquer algorithm

This project uses Emscripten to compile C code into JavaScript.

For an online version, see https://sgalal.github.io/knights-tour-visualization/.

Project Structure

Source files: src
For test: test
For web pages: index.html, index.js, index.css

Build

Prerequisite: Emscripten
Build: emcc -std=c11 -Weverything -Werror -Wno-unused-function -Wno-language-extension-token -O2 -s ASSERTIONS=1 -s EXPORTED_FUNCTIONS='["_getNextPointSerialize"]' -s EXTRA_EXPORTED_RUNTIME_METHODS='["ccall","cwrap"]' -o tour.js src/tour.c
Test: clang -std=c11 -Weverything -Werror -Wno-language-extension-token -DDEBUG -o tour src/tour.c test/tour_tb.c && ./tour

Implementation

Algorithm

The code is an implementation of Parberry, Ian. "An efficient algorithm for the Knight's tour problem." Discrete Applied Mathematics 73.3(1997):251-260.

A knight’s tour is called closed if the last square visited is also reachable from the first square by a knight’s move.

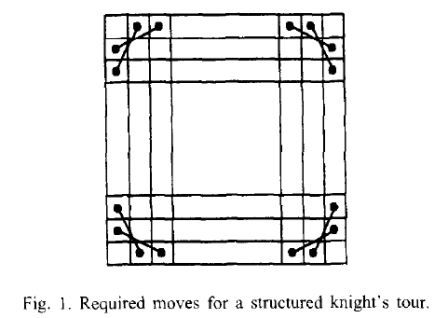
A knight’s tour is said to be structured if it includes the knight’s moves shown in Fig. 1.

An n * n chessboard has a closed knight's tour iff n ≥ 6 is even.

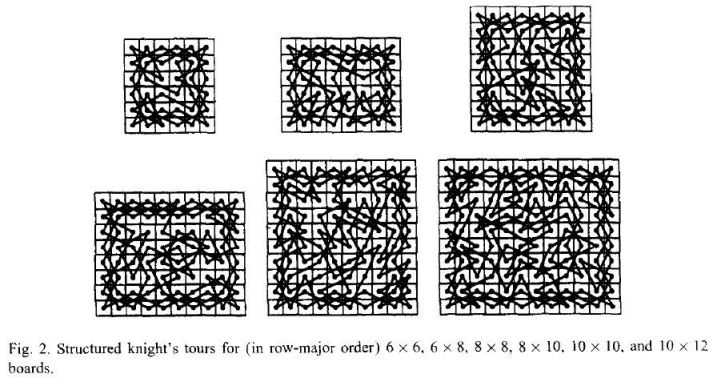
For board size of 6 * 6, 6 * 8, 8 * 8, 8 * 10, 10 * 10, and 10 * 12, we have already found structured, closed knight’s tours, which are shown in Fig. 2.

This means the problem is already solved when n ∈ {6, 8, 10}.

For larger n, divide the chess board into parts to meet the sizes above. For instance, a board with n = 42 can be divided as follows:

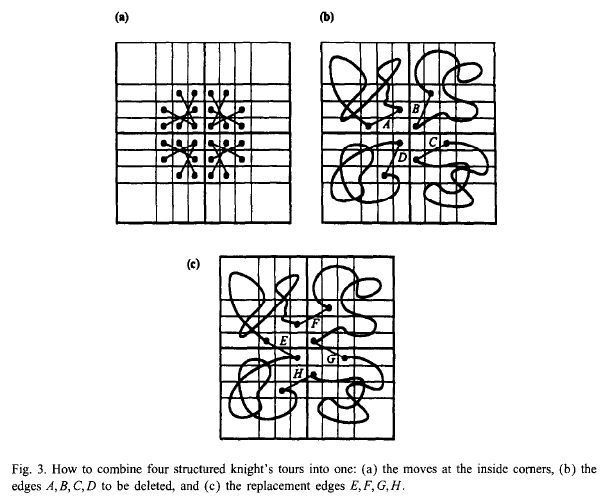
Then connect the parts together. Since all the parts are structured, we can combine them by substitute the directions on the corners:

Data Structure

Since every point is connected with other two points, and there are only 8 possible directions (from 0 to 7):

The 6 pre-defined tours are stored in 2-dimensional arrays.