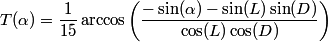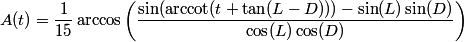In His Name, the Most High
Port of the code from http://www.praytimes.org into dotnet core library.
Muslims perform five prayers a day. Each prayer is given a certain prescribed time during which it must be performed. This document briefly describes these times and explains how they can be calculated mathematically.
To determine the exact period for each prayer (and also for fasting), we need to determine ten points of time per a day. These times are defined in the following table:
| Time | Definition |
|---|---|
| Imsak | The time to stop eating when fasting (in Ramadhan), slightly before Fajr. |
| Fajr | At the actual break of dawn. |
| Sunrise | The time at which the first part of the Sun appears above the horizon. |
| Dhuha | The time at which the Sun fully appears above the horizon (i.e. the completion of Sunrise). |
| Dhuhr | When the Sun begins to decline after reaching its highest point in the sky. |
| Asr | The time when the length of any object's shadow reaches a factor (usually 1 or 2) of the length of the object itself plus the length of that object's shadow at noon. |
| Sunset | The time at which the Sun disappears below the horizon. |
| Maghreb | Soon after sunset. |
| Isha | The time at which darkness falls, and there is no scattered light in the sky. |
| Midnight | The mean time from sunset to sunrise (or from Maghreb to Fajr, in some schools of thought). |
What follows is information on how to calculate the above times mathematically for any location if the coordinates of the site are known. This forms the basis of his this library/API works.
There are two astronomical measures that are essential for computing prayer times. These two measures are the equation of time and the declination of the Sun.
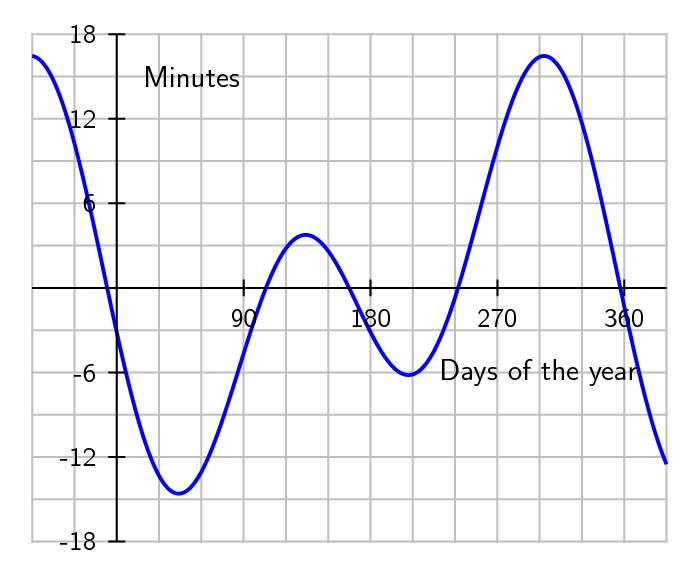
The equation of time is the difference between time as read from a sundial and a clock. It results from an apparent irregular movement of the Sun caused by a combination of the obliquity of the Earth's rotation axis and the eccentricity of its orbit. The sundial can be ahead (fast) by as much as 16min 33s (around November 3) or fall behind by as much as 14min 6s (around February 12), as shown in the following graph:
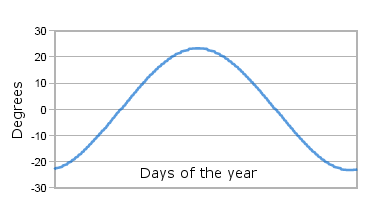
The declination of the Sun is the angle between the rays of the sun and the plane of the Earth's equator. The declination of the Sun changes continuously throughout the year. This is a consequence of the Earth's tilt (that is the difference in its rotational and revolutionary axes).
The above two astronomical measures can be obtained accurately from The Star Almanac, or can be calculated approximately. The following algorithm from U.S. Naval Observatory computes the Sun's angular coordinates to an accuracy of about 1 arcminute within two centuries of 2000.
d = jd - 2451545.0; // jd is the given Julian date
g = 357.529 + 0.98560028* d;
q = 280.459 + 0.98564736* d;
L = q + 1.915* sin(g) + 0.020* sin(2*g);
R = 1.00014 - 0.01671* cos(g) - 0.00014* cos(2*g);
e = 23.439 - 0.00000036* d;
RA = arctan2(cos(e)* sin(L), cos(L))/ 15;
D = arcsin(sin(e)* sin(L)); // declination of the Sun
EqT = q/15 - RA; // equation of timeTo calculate the prayer times for a given location, we need to know the latitude (Lat) and the longitude (Lng) of the location, along with the local Time zone for that location.
We also obtain the equation of time (EqT) and the declination of the Sun (D) for a given date using the algorithm mentioned above.
Dhuhr can be calculated easily using the following formula:
Dhuhr = 12 + TimeZone - Lng/15 - EqT.The above formula indeed calculates the midday time, when the Sun reaches its highest point in the sky. A slight margin is usually considered for Dhuhr as explained below:
Dhuhr has been defined in several ways in the fiqh (Islamic Judicial Law) literature:
- When the Sun begins to decline (Zawaal) after reaching its highest point in the sky.
- When the shadow of an indicator (a vertical stick) reaches its minimum length and starts to increase.
- When the Sun's disk comes out of its zenith line, which is a line between the observer and the center of the Sun when it is at the highest point.
The first and the second definitions are equivalent, as the shadow length has a direct correlation to the Sun's elevation in the sky via the following formula:
ShadowLength = Object Height × cot(SunAngle). The Sun's angle is a continuous function over time and has only one peak point (the point at which the tangent to its curve has zero slope) which is realized exactly at midday. Therefore, according to the first two definitions, Dhuhr begins immediately after the midday.
The third definition is slightly different from the previous two definitions. According to this definition, Sun must passes its zenith line before Dhuhr starts. We need the following information to calculate this time:
- The radius of the Sun (r): 695,500 km
- Distance between the Sun and the Earth (d): 147,098,074 km to 152,097,701 km
Having r and d, the time t needed for Sun to pass its zenith line can be computed using the following formula:
t = arctan(r/d) / 2π × 24 × 60 × 60The maximum value obtained by the above formula (which corresponds to the minimum Sun-Earth distance) is 65.0 seconds. Therefore, it takes approximately 1 minute until Sun's disk comes out of its zenith that should be considered into consideration for calculating Dhuhr, if the third definition is used.
There are three definitions for the Dhuhr time as described above. According to the first two definitions, Dhuhr = midday, and according to the third definition, Dhuhr = midday + 65 sec.
The time difference between the mid-day and the time at which sun reaches an angle α below the horizon can be computed using the following formula:
Astronomical sunrise and sunset occurs at α=0.
However, due to the refraction of light by terrestrial atmosphere, actual sunrise appears slightly before astronomical sunrise, and actual sunset occurs after astronomical sunset.
Actual sunrise and sunset can be computed using the following formulae:
Sunrise = Dhuhr - T(0.833)
Sunset = Dhuhr + T(0.833) If the observer's location is higher than the surrounding terrain, we can consider this elevation into consideration by increasing the above constant 0.833 by 0.0347 × sqrt(h), where h is the observer's height in meters.
This would make the fomulae:
Sunrise = Dhuhr - T(0.8333 + (0.0347 * sqrt(h)))
Sunrise = Dhuhr + T(0.8333 + (0.0347 * sqrt(h)))There are differing opinions on what angle to be used for calculating Fajr and Isha.
The following table shows several conventions currently in use in various countries:
| Method Code | Convention | Fajr Angle | Isha Angle | Regions Using Convention |
|---|---|---|---|---|
| MWL | Muslim World League | 18° | 17° | Europe, Far East, parts of US |
| ISNA | Islamic Society of North America (ISNA) | 15° | 15° | North America (US and Canada) |
| EGYPT | Egyptian General Authority of Survey | 19.5° | 17.5° | Africa, Syria, Lebanon, Malaysia |
| MAKKAH | Umm al-Qura University, Makkah | 18.5° (was 19° before December 2008/Muharram 1430) | 90mins after Maghreb (120m during Ramadhan) | Arabian Peninsula |
| KARACHI | University of Islamic Sciences, Karachi | 18° | 18° | Pakistan, Afganistan, Bangladesh, India |
| TEHRAN | Institute of Geophysics, University of Tehran | 17.7° | 14° (the Isha angle is not explicitly defined in the Tehran method) | Iran, Some Shia communities |
| JAFARI | Shia Ithna Ashari, Leva Research Institute, Qum | 16° | 14° | Some Shia communities worldwide |
| SINGAPURA | Majlis Ugama Islam Singapura | 20° | 18° | Muslim communities in Singapore |
| UOIOOF | Union of Islamic Organisations of France | 12° | 12° | Some Muslim communities in France and parts of Europe |
| JAKIM | Department of Islamic Advancement, Malaysia (JAKIM) | 20° | 18° | Muslim communities in Malaysia |
As an example, according the Shia Ithna Ashari, Leva Research Institute, Qum:
Fajr = Dhuhr - T(16) and Isha = Dhuhr + T(14)There are two main opinions on how to calculate Asr time. The majority of schools (including Shafi'i, Maliki, Ja'fari, and Hanbali) say it is at the time when the length of any object's shadow equals the length of the object itself plus the length of that object's shadow at noon.
The dominant opinion in the Hanafi school says that Asr begins when the length of any object's shadow is twice the length of the object plus the length of that object's shadow at noon.
The following formula computes the time difference between the mid-day and the time at which the object's shadow equals t times the length of the object itself plus the length of that object's shadow at noon:
Therefore, in the first four schools of thought the formula would be:
Asr = Dhuhr + A(1)Whereas in the Hanafi school the formula would be:
Asr = Dhuhr + A(2)In the opinion of the Sunni schools of Islamic Judicial Law, the time for Maghreb prayer begins once the Sun has completely set beneath the horizon, that is:
Maghreb = SunsetIt should be noted that within the Sunni Judicial Law, some calculators suggest 1 to 3 minutes after Sunset on the basis of a precaution.
The Shia Juristis rather suggest that as long as the redness in the eastern sky appearing after sunset has not passed overhead, Maghreb prayer should not be performed. It is usually taken into consideration by assuming a twilight angle (as shown in the tables above):
Maghreb = Dhuhr + T(4). Midnight is generally calculated as the mean time from Sunset to Sunrise:
Midnight = 1/2(Sunrise - Sunset)However, the Shia Jurists opine that the juridical midnight (the ending time for performing Isha prayer) is the mean time from Sunset to Fajr:
Midnight = 1/2(Fajr - Sunset)In locations at higher latitude, twilight may persist throughout the night during some months of the year.
In these abnormal periods, the determination of Fajr and Isha is not possible using the usual formulas as described above. In order to overcome this problem, several solutions have been proposed, three of which are described below:
In this method, the period from sunset to sunrise is divided into two halves. The first half is considered to be the "night" and the other half as "day break". Fajr and Isha in this method are assumed to be at mid-night during the abnormal periods.
In this method, the period between sunset and sunrise is divided into seven parts. Isha begins after the first one-seventh part, and Fajr is at the beginning of the seventh part.
This is an intermediate solution, used by some recent prayer time calculators.
var α == TheTwilightAngleForIsha,
var t = α/60. The period between sunset and sunrise is divided into t parts. Isha begins after the first part.
For example, if the twilight angle for Isha is 15, then Isha begins at the end of the first quarter (15/60) of the night.
Time for Fajr is calculated similarly.
In case Maghreb is not equal to Sunset, we can apply the above rules to Maghreb as well to make sure that Maghreb always falls between Sunset and Isha during the abnormal periods.
This project is built on the excellent work PrayTimes.org by Hamid Zarrabi-Zadeh. I have taken the formulae and calculations, sanity checked them as applicable, and examined the source code that various other contributers have written - found at Prayer Times Code Snippets. However, given that some of the code is extremely out-dated, and in some cases doesn't work as it should, I have decided to re-write the source code - using Microsoft .NET Core, and provide the Class Library via Nuget, and an API that can be used by anyone...
The source code for the Library (nuget Package) will be available here on Github, as will the source code for the Web API (and a sample application to consume the API).
If you are going to use use this code commercially or privately, please at the very least let me know and be sure to follow the guidelines of the LGPL license for the original praytimes.org code, and be sure to credit them and link to them - as well as this repository.
I will be setting up a Discord channel, where discussions on the code and related matters can be had, and this will be linked to when appropriate.
Thanks to the work done by Zulfahmi Ahmad, this code has been significantly improved and the calculation methods for Singapore and Malaysia have been added.
There are also many unit tests that can be used to verify calculations; as well as a Console App that can be used to display the times for prayer.
A set of calender conversion methods and classes has now been added (based of the excellent work by Milad Shahabfar's Persia.NET-Core. This work was brought into this library, since the Persia.NET-Core library is purely dotnet core 5, and therefore cannot be used in Xamarin based projects (or projects that don't support dotnet core 5 and need dotnet standard 2+).
A sample of how to use this can be found in the Console App Project.
It should be noted that while every effort has been taken to ensure the veracity of the calculations provided by the library, and a great deal of testing has been placed (Unit Tests will be provided in the source code as it is released), this library is provided AS-IS, with no warrenty or claim that it is completley accurate and without flaws.
More details will be added as the project proceeds.
The following repos have been very useful in getting this code working: