Shape-supervised dimension reduction: Extracting geometry and physics associated features with geometric moments
Shape reparameterisation with geometric and physics-informed latent variables for shape optimisation
Shahroz Khan*, Panagiotis Kaklis, Andrea Serani, Matteo Diez, Konstantinos Kostas
[Paper] [Pre-Prints] [Presentation] [Video]
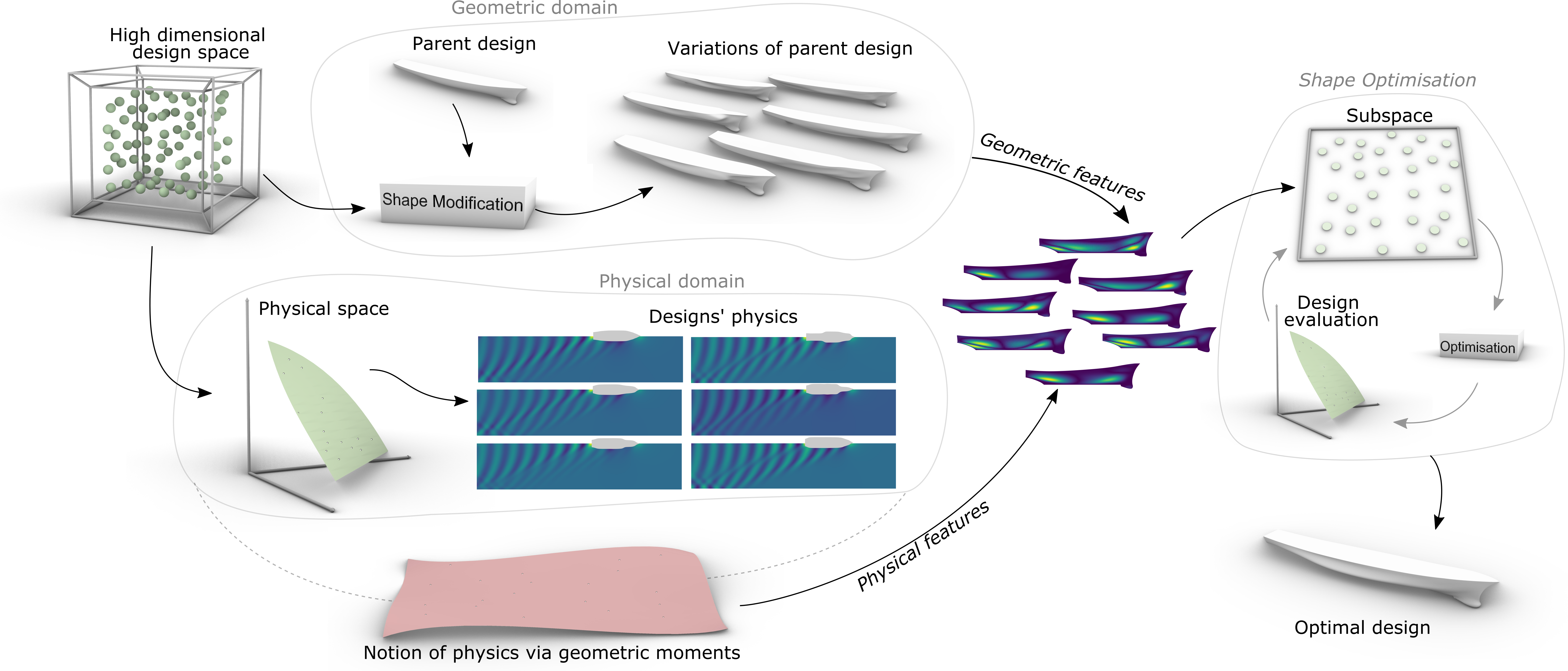
Despite the success of design space dimensionality reduction for accelerating computationally demanding shape optimisation processes, the existing approaches, such as PCA, Active-Subspace Method, AutoEncoders, etc., suffer from two critical drawbacks: i) low-levels of robustness, i.e., a non-negligible percentage of designs in the reduced dimensionality subspace corresponds to invalid/infeasible instances, and ii) inability to capture high-level structure information, i.e., high-level features, associated to physics, which would considerably improve performance, are not captured.
Therefore, we propose a shape-supervised dimension reduction (SSDR) approach. To simultaneously tackle these deficiencies, SSDR uses higher-level information about the shape in terms of its geometric integral properties, such as geometric moments and their invariants. Their usage is based on the fact that moments of a shape are intrinsic features of its geometry, and they provide a unifying medium between geometry and physics. To enrich the subspace with latent features associated with shape's geometrical features and physics, we also evaluate a set of composite geometric moments, using the divergence theorem, for appropriate shape decompositions. These moments are combined with the shape modification function to form a Shape Signature Vector (SSV) uniquely representing a shape. Afterwards, the generalised Karhunen-Loève expansion is applied to SSV, embedded in a generalised (disjoint) Hilbert space. This results in the extraction of latent variables retaining the highest geometric and physical variance. These variables are used as new parameters of the shape, which can be used to construct a lower-dimensional shape-supervised subspace. The new subspace
- has not only enhanced representation capacity and compactness to produce a valid and diverse set of design alternatives, respectively, but
- is also physically informed to improve the convergence rate of the shape optimiser towards an optimal solution.
The code of SSDR has been tested on the Matlab 2020a. It should work on any other version of the Matlab. However, SSDR's functions, KLE.m and sthOrderGeometricMoment.m, use Matlab's gpuArray and parfor, respectively, from Parallel Computing Toolbox, which may not be compatible for your version of the Matlab version.
If you do not have Parallel Computing Toolbox then you can set variable useGPU to zero in KLE.m. Also, change parfor in sthOrderGeometricMoment.m to for at line 48 and 61.
SSDR does not have any external dependencies.
The core of SSDR is composed of two main functionalities, evaluation of geometric moments, creation of shape-signature vector (SSV) and implementation of Karhunen-Loève expansion of SSV.
Construction of SSV involves a design grid and geometric moments of sth-order. An sth-order geometric moment M_pqr can be evaluated as follows:
where s=p+q+r. Moreover, all the moments of a certain order can be defined as follows:
where M^s is the sth-order moment vector used in SSV.
- Use
sthOrderGeometricMoment.mfunction to evaluate sth-order M_pqr. - Use
sthOrderGeometricMomentVector.mfunction to evaluate sth-order M^s.
The above functions take a closed 3D triangulated mesh in the .stl formate to evaluate geometric moments. Test these functions for a wing and a ship model.
Once SSV is constructed, KLE.m can be used to extract the geometrically- and functionally active latent variables.
For further details on the usage of these functions and the implementation of SSDR, use the example file example_shapeSupSubspace.m, which implements it on a 3D wing example. To run the example, first download the Datasets (wingMoments, wingSamples) and place them in the working folder.
Once latent variables are constructed, use the evlSubspaceLimits.m function to build the shape-supervised subspace, which can later be used for shape optimisation against any physical quantity of interest.
To install the SSDR package, simply download the folder or open the Matlab to clone the repository with the command
https://github.com/shahrozkhan66/SSDR.gitusing the following steps:
- Open Matlab
- On the Home tab, click New > Project >> From Git. The New Project From Source Control dialog box opens.
- Enter
https://github.com/shahrozkhan66/SSDR.gitinto the Repository path field. - In the Sandbox field, select the working folder where you want to put the retrieved files for your new project.
- Click Retrieve >> OK >> Set Up Project >> Next >> Finish.
- Download the Datasets (wingMoments, wingSamples) and place them in the working folder.
- Run example
example_shapeSupSubspace.m.
If you have questions or feedback, contact Shahroz Khan.
This work has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant "GRAPES: learninG, pRocessing And oPtimising shapES" (agreement No. 860843).
Distributed under the GNU GENERAL PUBLIC LICENSE. See LICENSE.txt for more information.