Lsystem is inspired by the book 'Algorithmic Beauty of Plants' (ABOP) by
Prusinkiewcz and Lindenmayer. Most of the systems described in the book can be
implemented with this package (and the missing features are coming soon).
Lsystem is quite general, supporting context-dependent, parameterized,
stochastic L-systems. I will write specific documentation when the feature set
is stable.
Specifying systems in Lsystem is currently a bit verbose (see the examples in
the following sections), but there are special handlers for the simplest
systems. Eventually I will write a full parser for the specification language
used in ABOP.
DOL-systems are deterministic, context-free, non-branching, and 2D. They can be expressed with the following 3 characters:
- 'F' - draw a line forward
- '-' - turn left
- '+' - turn right
With each iteration of the system, each 'F' is replaced by a new string. In ABOP syntax, the first example below can be specified as
n=3 d=90
F-F-F-F
F -> F-F+F-F+F
where n is the number of steps to take, d is the degree of the turns,
F-F-F-F is the original string, and F -> F-F+F-F+F is a rule for replacing
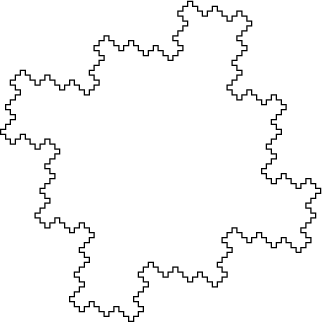
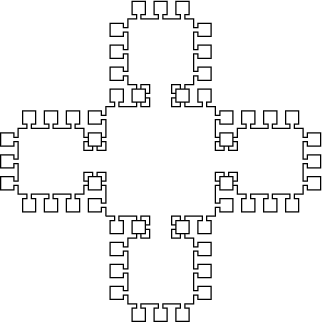
F at each step. These systems can be used to generate simple fractal images.
import Lsystem
import System.Random
render' :: String -> System -> IO ()
render' = renderSystem (mkStdGen 42) (400,400)
main :: IO ()
main = do
render' "d1.svg" $ transDolSys 3 90 "F-F-F-F" "F-F+F-F+F"
render' "d2.svg" $ transDolSys 2 90 "F-F-F-F" "F+FF-FF-F-F+F+FF-F-F+F+FF+FF-F"
render' "d3.svg" $ transDolSys 3 90 "F-F-F-F" "FF-F--F-F"
render' "d4.svg" $ transDolSys 3 90 "F-F-F-F" "F-F-F+F+F-F-F+F+F"
render' "d5.svg" $ transDolSys 2 90 "F-F-F-F" "FF+F+F-FFF-FFF-FFF-F+F+FF"
render' "d6.svg" $ transDolSys 3 90 "F-F-F-F" "F+F+F-F-F+F-F-F+F-F-F+F+F"
render' "d7.svg" $ transDolSys 4 90 "F-F-F-F" "FF-F+F+F-F"
render' "d8.svg" $ transDolSys 4 90 "F-F-F-F" "FF-F-F+F+F-F+F+F-F+F+F-F-FF"
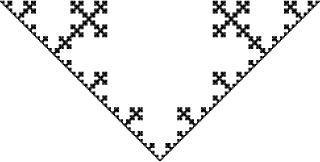
render' "d9.svg" $ transDolSys 5 90 "F" "F+F-F-F+F"L-systems can be made stochastic be adding probabilistic rules. A probabilistic rule is a set of rules associated with probabilities, where the probabilities must sum to a number less than or equal to 1 (with the implicit default rule of N -> N making up the difference).
import Lsystem
import System.Random
render' :: String -> System -> IO ()
render' = renderSystem (mkStdGen 42) (400,400)
-- Where the arguments are:
-- 1. number of steps
-- 2. angle
-- 3. initial state
-- 4. weighted list of random replacements
s1 = transSolSys 12 45 "F" [(0.4, "FF"), (0.5, "-F"), (0.1, "FF-FF-FF-FF")]
main :: IO ()
main = do
render' "s1.svg" s1I currently don't have any sugar for branching. So I will do this the hard way.
import Lsystem
import System.Random
render' :: String -> System -> IO ()
render' = renderSystem (mkStdGen 42) (400,400)
-- -- This example is taken from ABOP pp. 25
-- n=5 d=25.7
-- F -> F[+F]F[-F]F
b1 = System {
systemBasis = [NodeDraw [] 1] -- F
, systemRules = [ -- F[+F]F[-F]F
DeterministicRule {
ruleContext = ignoreContext
, ruleCondition = unconditional
, ruleMatch = matchF
, ruleReplacement = constantReplacement [
NodeDraw [] 1 ------------------ F
, NodeBranch [[ ------------------ [+F]
NodeRotate [] (-25.7) 0 0
, NodeDraw [] 1
]]
, NodeDraw [] 1 ------------------ F
, NodeBranch [[ ------------------ [-F]
NodeRotate [] 25.7 0 0
, NodeDraw [] 1
]]
, NodeDraw [] 1 ------------------ F
]
}
]
, systemSteps = 5
}
main :: IO ()
main = do
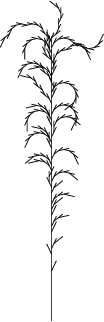
render' "b1.svg" b1Putting together the previous two examples, we can make more plant-like constructions
-- n=5 f=22.5
-- X
-- X -> F-[[X]+X]+F[+FX]-X
-- F -> FF
dummy = System {
systemBasis = [x]
, systemRules = [
DeterministicRule {
ruleContext = ignoreContext
, ruleCondition = unconditional
, ruleMatch = matchDummy [] "X"
, ruleReplacement = constantReplacement [
f, m -- F-
, NodeBranch [[NodeBranch [[x]], p, x]] -- [[X]+X]
, p, f -- +F
, NodeBranch [[p,f,x]] -- [+FX]
, m, x -- -X
]
},
DeterministicRule {
ruleContext = ignoreContext
, ruleCondition = unconditional
, ruleMatch = matchF
, ruleReplacement = constantReplacement [f,f]
}
]
, systemSteps = 5
} where
p = NodeRotate [] 22.5 0 0
m = NodeRotate [] (-22.5) 0 0
f = NodeDraw [] 1
x = NodeDummy [] "X"-- n=26 d=25.75
-- ignore +-F
-- F1F1F1
--
-- 0 0 0 -> 0
-- 0 0 1 -> 1[+F1F1]
-- 0 1 0 -> 0
-- 0 1 1 -> 1
-- 1 0 0 -> 0
-- 1 0 1 -> 1F1
-- 1 1 0 -> 0
-- 1 1 1 -> 0
-- * - * -> +
-- * + * -> -
contextual = System {
systemBasis = [f,a,f,b,f,b]
, systemRules = [
StochasticRule [(0.97, DeterministicRule c000 unconditional isA [b] )] -- 0 0 0 -> 1
, StochasticRule [(0.97, DeterministicRule c001 unconditional isA [a] )] -- 0 0 1 -> 0
, StochasticRule [(0.97, DeterministicRule c010 unconditional isB [a] )] -- 0 1 0 -> 0
, StochasticRule [(0.97, DeterministicRule c011 unconditional isB [b,f,b] )] -- 0 1 1 -> 1F1
, StochasticRule [(0.97, DeterministicRule c100 unconditional isA [b] )] -- 1 0 0 -> 1
, StochasticRule [(0.97, DeterministicRule c101 unconditional isA [b, NodeBranch [[ p,f,b,f,b ]]] )] -- 1 0 1 -> 1[+F1F1]
, StochasticRule [(0.97, DeterministicRule c110 unconditional isB [b] )] -- 1 1 0 -> 1
, StochasticRule [(1.00, DeterministicRule c111 unconditional isB [a] )] -- 1 1 1 -> 0
, StochasticRule [(0.97, DeterministicRule ignoreContext unconditional isP [m] )] -- * - * -> +
, StochasticRule [(0.98, DeterministicRule ignoreContext unconditional isM [p] )] -- * + * -> -
]
, systemSteps = 27
} where
f = NodeDraw [] 1
a = NodeDummy [] "0"
b = NodeDummy [] "1"
p = NodeRotate [] 25.75 0 0
m = NodeRotate [] (-25.75) 0 0
ss = [p,m,f]
isA = matchDummy [] "0"
isB = matchDummy [] "1"
isP :: Node -> a -> Maybe a
isP (NodeRotate _ a _ _) x | a > 0 = Just x
| otherwise = Nothing
isP _ _ = Nothing
isM :: Node -> a -> Maybe a
isM (NodeRotate _ a _ _) x | a < 0 = Just x
| otherwise = Nothing
isM _ _ = Nothing
c000 = contextMatch ss [a] [a]
c001 = contextMatch ss [a] [b]
c010 = contextMatch ss [a] [a]
c011 = contextMatch ss [a] [b]
c100 = contextMatch ss [b] [a]
c101 = contextMatch ss [b] [b]
c110 = contextMatch ss [b] [a]
c111 = contextMatch ss [b] [b] The replacement string is a function of the original symbol and the context. Each symbol holds a vector of doubles, which can be used pass extra information. This example comes from ABOP pp. 47.
par1 = System {
systemBasis = basis
, systemRules = [
DeterministicRule {
ruleContext = ignoreContext
, ruleCondition = unconditional
, ruleMatch = matchDummy "A"
, ruleReplacement = r_repl
}
]
, systemSteps = 10
} where
r = 1.456
p = NodeRotate [] 85 0 0
m = NodeRotate [] (-85) 0 0
-- A(1)
basis = [NodeDummy [1] "A"]
-- F(s)[+A(s/R)][-A(s/R)]
r_repl _ _ (NodeDummy [s] _) = [
NodeDraw [] s -- F(s)
, NodeBranch [
[p, NodeDummy [s/r] "A"] -- [+A(s/R)]
, [m, NodeDummy [s/r] "A"] -- [-A(s/R)]
]
]#define c 1.0
#define p 0.3
#define q c - p
#define h sqrt (p * q)
w : f(0,1)
p1 : F(x,t) : t = 0 : F(x*p, 2) + F(x*h, 1) -- F(x*h, 1) + F(x*q, 0)
p2 : F(x,t) : t > 0 : F(x, t-1)
par2 = System {
systemBasis = basis
, systemRules = [
DeterministicRule {
ruleContext = ignoreContext
, ruleCondition = r1_cond
, ruleMatch = isF
, ruleReplacement = r1_repl
}
, DeterministicRule {
ruleContext = ignoreContext
, ruleCondition = r2_cond
, ruleMatch = isF
, ruleReplacement = r2_repl
}
]
, systemSteps = 8
} where
c = 1.0
p = 0.3
q = c - p
h = sqrt (p * q)
p' = NodeRotate [] 86 0 0
m' = NodeRotate [] (-86) 0 0
-- f(0,1)
basis = [NodeDraw [0] 1]
-- t = 1
r1_cond _ _ (NodeDraw [t] _) x
| t == 0 = Just x
| otherwise = Nothing
r1_cond _ _ _ _ = Nothing
-- F(x*p, 2) + F(x*h, 1) - - F(x*h, 1) + F(x*q, 0)
r1_repl _ _ (NodeDraw [t] x) = [
NodeDraw [2] (x*p) -- F(x*p, 2)
, p' -- +
, NodeDraw [1] (x*h) -- F(x*h, 1)
, m' -- -
, m' -- -
, NodeDraw [1] (x*h) -- F(x*h, 1)
, p' -- +
, NodeDraw [0] (x*q) -- F(x*q, 0)
]
-- t > 0
r2_cond _ _ (NodeDraw [t] _) x
| t > 0 = Just x
| otherwise = Nothing
r2_cond _ _ _ _ = Nothing
-- F(x, t-1)
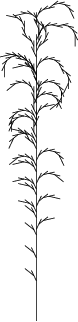
r2_repl _ _ (NodeDraw [t] x) = [ NodeDraw [t-1] x ]Modeling realistic trees requires two new features: variation in line width and 3-dimensional systems. This example is taken from ABOP pp. 60.
#define d1 94.74 /* divergence angle 1 */
#define d2 132.62 /* divergence angle 2 */
#define a 18.95 /* branching angle */
#define lr 1.109 /* elongation rate */
#define vr 1.732 /* width increase rate */
w = !(1)F(200)/(45)A
A : * -> !(vr )F(50)[&(a)F(50)A]/(d1)
[&(a)F(50)A]/(d2)[&(a)F(50)A]
F(l) : * -> F(l*lr )
!(w) : * -> !(w*vr )
- deterministic
- stochastic
- branching
- dummy variables
- context sensitive
- parametric
- stochastic sugar
- deterministic sugar
- branching sugar
- parametric sugar
- context sensitive sugar
- 2D visualization
- 3D handling
- 3D visualization
- animation
- polygons
- colors and such
- ABOP language parsing