Generalized Intersection Over Union: A Metric and a Loss for Bounding Box Regression
- It is good to learn by evaluation metrics (ex. IOU)
- IOU Loss gives only error between 0 and 1. However, using GIoU can give errors from 0 to 2.
- Results are better with the YOLO structure than with the RCNN structure.
# Hand-drawn picture example XD
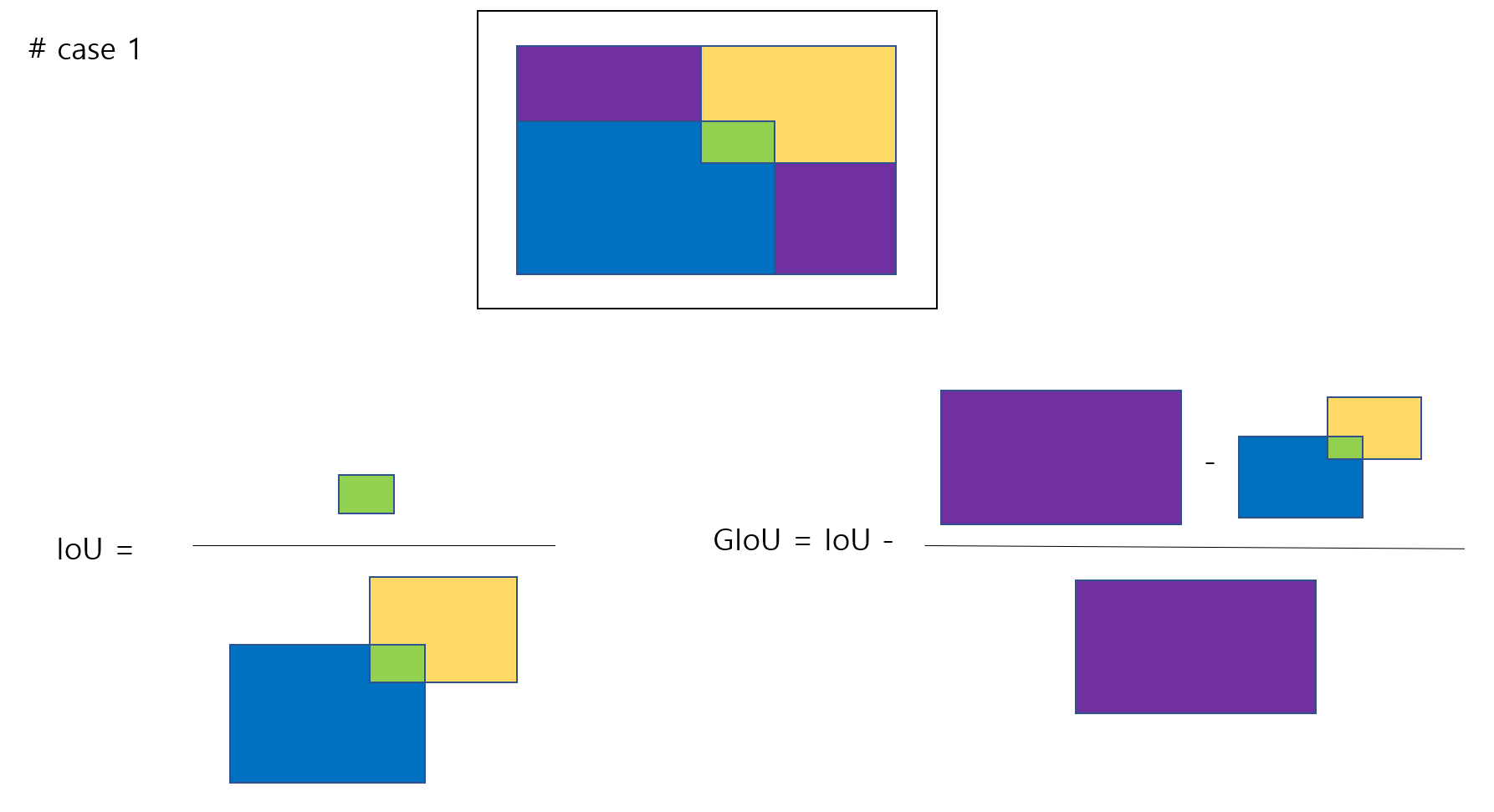
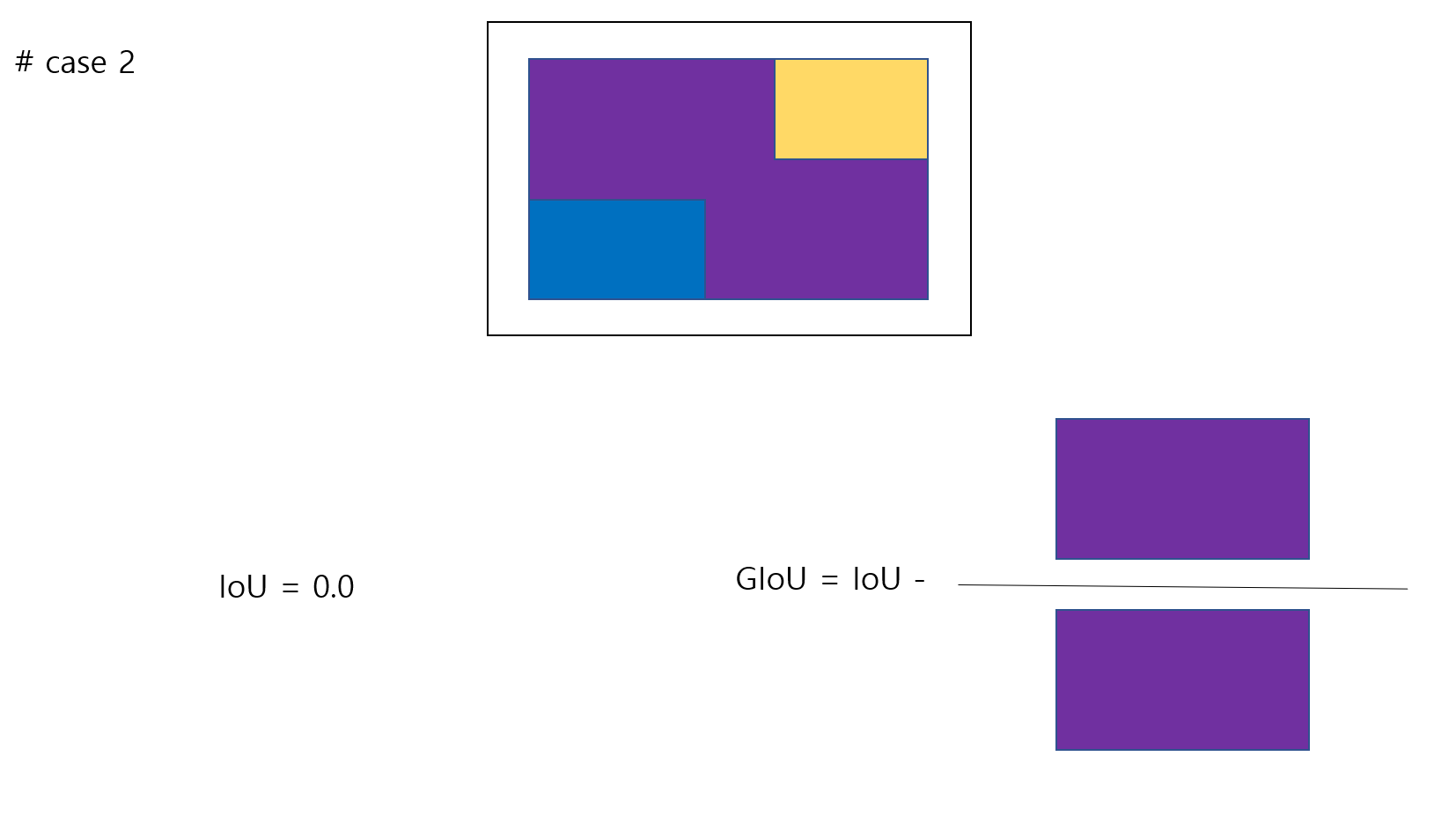
'''
# Copyright (C) 2019 * Ltd. All rights reserved.
# author : SangHyeon Jo <josanghyeokn@gmail.com>
GIoU = IoU - (C - (A U B))/C
GIoU_Loss = 1 - GIoU
'''
def GIoU(bboxes_1, bboxes_2):
# 1. calulate intersection over union
area_1 = (bboxes_1[..., 2] - bboxes_1[..., 0]) * (bboxes_1[..., 3] - bboxes_1[..., 1])
area_2 = (bboxes_2[..., 2] - bboxes_2[..., 0]) * (bboxes_2[..., 3] - bboxes_2[..., 1])
intersection_wh = tf.minimum(bboxes_1[:, :, 2:], bboxes_2[:, :, 2:]) - tf.maximum(bboxes_1[:, :, :2], bboxes_2[:, :, :2])
intersection_wh = tf.maximum(intersection_wh, 0)
intersection = intersection_wh[..., 0] * intersection_wh[..., 1]
union = (area_1 + area_2) - intersection
ious = intersection / tf.maximum(union, 1e-10)
# 2. (C - (A U B))/C
C_wh = tf.maximum(bboxes_1[..., 2:], bboxes_2[..., 2:]) - tf.minimum(bboxes_1[..., :2], bboxes_2[..., :2])
C_wh = tf.maximum(C_wh, 0.0)
C = C_wh[..., 0] * C_wh[..., 1]
giou = ious - (C - union) / tf.maximum(C, 1e-10)
return giou