To perform data analysis on sample titanic dataset.
This dataset contains demographics and passenger information from 891 of the 2224 passengers and crew on board the Titanic. You can view a description of this dataset on the Kaggle website, where the data was obtained (https://www.kaggle.com/c/titanic/data).
"One of the reasons that the shipwreck led to such loss of life was that there were not enough lifeboats for the passengers and crew. Although there was some element of luck involved in surviving the sinking, some groups of people were more likely to survive than others, such as women, children, and the upper-class."
What factors made people more likely to survive?
- Were social-economic standing a factor in survival rate?
- Did age, regardless of sex, determine your chances of survival?
- Did women and children have preference to lifeboats (survival)?
- How did children with nannies fare in comparison to children with parents?
Assumption: We are going to assume that everyone who survived made it to a life boat and it wasn't by chance or luck.
(from https://www.kaggle.com/c/titanic)
- survival Survival (0 = No; 1 = Yes)
- pclass Passenger Class (1 = 1st; 2 = 2nd; 3 = 3rd)
- name Name
- sex Sex
- age Age
- sibsp Number of Siblings/Spouses Aboard
- parch Number of Parents/Children Aboard
- ticket Ticket Number
- fare Passenger Fare
- cabin Cabin
- embarked Port of Embarkation (C = Cherbourg; Q = Queenstown; S = Southampton)
SPECIAL NOTES:
-
Pclass is a proxy for socio-economic status (SES) 1st ~ Upper; 2nd ~ Middle; 3rd ~ Lower
-
Age is in Years; Fractional if Age less than One (1) If the Age is Estimated, it is in the form xx.5
With respect to the family relation variables (i.e. sibsp and parch) some relations were ignored. The following are the definitions used for sibsp and parch.
- Sibling: Brother, Sister, Stepbrother, or Stepsister of Passenger Aboard Titanic
- Spouse: Husband or Wife of Passenger Aboard Titanic (Mistresses and Fiances Ignored)
- Parent: Mother or Father of Passenger Aboard Titanic
- Child: Son, Daughter, Stepson, or Stepdaughter of Passenger Aboard Titanic
Other family relatives excluded from this study include cousins, nephews/nieces, aunts/uncles, and in-laws. Some children travelled only with a nanny, therefore parch=0 for them. As well, some travelled with very close friends or neighbors in a village, however, the definitions do not support such relations.
import pandas
import matplotlib.pyplot as plt
data = pandas.read_csv('titanic_data.csv')
for column in data:
print columnPassengerId
Survived
Pclass
Name
Sex
Age
SibSp
Parch
Ticket
Fare
Cabin
Embarked
data.head()| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
Note: Some values for Age are NaN, while ticket and cabin values are alphanumeric and also missing values with NaN. Not a big deal but good to know. Based on current questions, will not require either Ticket or Cabin data.
Additional potential questions from reading data and data description
-
How did children with nannies fare in comparison to children with parents. Did the nanny "abandon" the child to save his/her own life?
- I would need additional information to determine if a child was indeed only on board with a nanny. For example, a child could be on board with an adult sibling. This would make Parch (parent) = 0 but it would be incorrect to say the child had a nanny.
- Need to review list for children with no siblings. These will be children with nannies; however, a child could have siblings and still have a nanny as well.
-
Did cabin location play a part in the survival rate without the consideration of class
- No data on where the cabins are actually located on the Titanic
- External source of this data could probably be found
flag = False
for entry in data['Survived']:
if entry not in [0, 1]:
print entry
flag = True
if flag == False:
print 'No inconsistent data'No inconsistent data
flag = False
for entry in data['Pclass']:
if entry not in [1, 2, 3]:
print entry
flag = True
if flag == False:
print 'No inconsistent data'No inconsistent data
flag = False
for entry in data['Sex']:
if entry not in ['male','female']:
print entry
flag = True
if flag == False:
print 'No inconsistent data'No inconsistent data
flag = False
for entry in data['Embarked']:
if entry not in ('C','Q','S'):
print entry
flag = True
if flag == False:
print 'No inconsistent data'nan
nan
Column embarked contains two 'NaN' values
flag = False
duplicates = data.duplicated()
for duplicate in duplicates:
if duplicate=='True':
print 'Duplicated Exists'
flag = True
if flag==False:
print 'No Duplicates'No Duplicates
data.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId 891 non-null int64
Survived 891 non-null int64
Pclass 891 non-null int64
Name 891 non-null object
Sex 891 non-null object
Age 714 non-null float64
SibSp 891 non-null int64
Parch 891 non-null int64
Ticket 891 non-null object
Fare 891 non-null float64
Cabin 204 non-null object
Embarked 889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.6+ KB
From the data description and questions to answer, I've determined that some dataset columns will not play a part in my analysis and these columns can therefore be removed. This will decluster the dataset and also help with processing performance of the dataset.
* PassengerId
* Name
* Ticket
* Cabin
I'll take a 2 step approach to data cleanup
1. Remove unnecessary columns
2. Fix missing and data format issues
Columns (PassengerId, Name, Ticket, Cabin) removed
titanic_data = data.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1)
titanic_data.head()| Survived | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | male | 22.0 | 1 | 0 | 7.2500 | S |
| 1 | 1 | 1 | female | 38.0 | 1 | 0 | 71.2833 | C |
| 2 | 1 | 3 | female | 26.0 | 0 | 0 | 7.9250 | S |
| 3 | 1 | 1 | female | 35.0 | 1 | 0 | 53.1000 | S |
| 4 | 0 | 3 | male | 35.0 | 0 | 0 | 8.0500 | S |
titanic_data.isnull().sum()Survived 0
Pclass 0
Sex 0
Age 177
SibSp 0
Parch 0
Fare 0
Embarked 2
dtype: int64
missing_age_bool = pandas.isnull(titanic_data['Age'])
titanic_data[missing_age_bool].head()| Survived | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | |
|---|---|---|---|---|---|---|---|---|
| 5 | 0 | 3 | male | NaN | 0 | 0 | 8.4583 | Q |
| 17 | 1 | 2 | male | NaN | 0 | 0 | 13.0000 | S |
| 19 | 1 | 3 | female | NaN | 0 | 0 | 7.2250 | C |
| 26 | 0 | 3 | male | NaN | 0 | 0 | 7.2250 | C |
| 28 | 1 | 3 | female | NaN | 0 | 0 | 7.8792 | Q |
missing_age_male = titanic_data[missing_age_bool]['Sex']=='male'
missing_age_female = titanic_data[missing_age_bool]['Sex']=='female'
print 'Number of missing age of male - ',missing_age_male.sum()
print 'Number of missing age of female - ',missing_age_female.sum()Number of missing age of male - 124
Number of missing age of female - 53
Missing Age data will affect Q2 - Did age, regardless of sex, determine your chances of survival? But graphing and summations shouldn't be a problem since they will be treated as zero(0) value. However, 177 is roughly 20% of our 891 sample dataset which seems like a lot to discount. Also, this needs to be accounted for if reviewing descriptive stats such as mean age.
Should keep note of the proportions across male and female...
- Age missing in male data: 124
- Age missing in female data: 53
data.describe()| PassengerId | Survived | Pclass | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|---|
| count | 891.000000 | 891.000000 | 891.000000 | 714.000000 | 891.000000 | 891.000000 | 891.000000 |
| mean | 446.000000 | 0.383838 | 2.308642 | 29.699118 | 0.523008 | 0.381594 | 32.204208 |
| std | 257.353842 | 0.486592 | 0.836071 | 14.526497 | 1.102743 | 0.806057 | 49.693429 |
| min | 1.000000 | 0.000000 | 1.000000 | 0.420000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 223.500000 | 0.000000 | 2.000000 | 20.125000 | 0.000000 | 0.000000 | 7.910400 |
| 50% | 446.000000 | 0.000000 | 3.000000 | 28.000000 | 0.000000 | 0.000000 | 14.454200 |
| 75% | 668.500000 | 1.000000 | 3.000000 | 38.000000 | 1.000000 | 0.000000 | 31.000000 |
| max | 891.000000 | 1.000000 | 3.000000 | 80.000000 | 8.000000 | 6.000000 | 512.329200 |
youngest_to_survive = titanic_data[titanic_data['Survived'] == 1]['Age'].min()
youngest_to_die = titanic_data[titanic_data['Survived'] == 0]['Age'].min()
oldest_to_survive = titanic_data[titanic_data['Survived'] == 1]['Age'].max()
oldest_to_die = titanic_data[titanic_data['Survived'] == 0]['Age'].max()
print 'Youngest_to_survive - ',youngest_to_survive
print 'Youngest_to_die - ',youngest_to_die
print 'Oldest_to_survive - ',oldest_to_survive
print 'Oldest_to_die - ',oldest_to_dieYoungest_to_survive - 0.42
Youngest_to_die - 1.0
Oldest_to_survive - 80.0
Oldest_to_die - 74.0
Data description states that Age can be fractional - Age is in Years; Fractional if Age less than One (1) If the Age is Estimated, it is in the form xx.5 - Therefore, 0.42 appears to be expected and normal data
Note: An interesting note is that all "new borns" survived.
Were social-economic standing a factor in survival rate?
group_by_class_survival = titanic_data.groupby(['Pclass', 'Survived', 'Sex']).size()
print group_by_class_survivalPclass Survived Sex
1 0 female 3
male 77
1 female 91
male 45
2 0 female 6
male 91
1 female 70
male 17
3 0 female 72
male 300
1 female 72
male 47
dtype: int64
def survival(pclass, sex):
group_by_class = titanic_data.groupby(['Pclass', 'Sex']).size()[pclass, sex].astype('float')
group_by_class_survived = titanic_data.groupby(['Pclass', 'Survived', 'Sex']).size()[pclass, 1, sex].astype('float')
print 'Total numbers of',sex,'of class',pclass,'-',group_by_class
print 'Total numbers of',sex,'of class',pclass,'who survived -',group_by_class_survived
survival_rate = ((group_by_class_survived/group_by_class)*100).round(2)
return survival_rate
print '\n\n'
print 'Effect of social economy in survival rate : \n'
print 'Class 1 - Male survival rate :\n',survival(1, 'male'),'%\n'
print 'Class 1 - Female survival rate \n:',survival(1, 'female'),'%\n'
print '-------------\n'
print 'Class 2 - Male survival rate :\n',survival(2, 'male'),'%\n'
print 'Class 2 - Female survival rate:\n',survival(2, 'female'),'%\n'
print '-------------\n'
print 'Class 3 - Male survival rate :\n',survival(3, 'male'),'%\n'
print 'Class 3 - Female survival rate :\n',survival(3, 'female'),'%\n'Effect of social economy in survival rate :
Class 1 - Male survival rate :
Total numbers of male of class 1 - 122.0
Total numbers of male of class 1 who survived - 45.0
36.89 %
Class 1 - Female survival rate
: Total numbers of female of class 1 - 94.0
Total numbers of female of class 1 who survived - 91.0
96.81 %
-------------
Class 2 - Male survival rate :
Total numbers of male of class 2 - 108.0
Total numbers of male of class 2 who survived - 17.0
15.74 %
Class 2 - Female survival rate:
Total numbers of female of class 2 - 76.0
Total numbers of female of class 2 who survived - 70.0
92.11 %
-------------
Class 3 - Male survival rate :
Total numbers of male of class 3 - 347.0
Total numbers of male of class 3 who survived - 47.0
13.54 %
Class 3 - Female survival rate :
Total numbers of female of class 3 - 144.0
Total numbers of female of class 3 who survived - 72.0
50.0 %
%matplotlib inline
titanic_data_survived = titanic_data
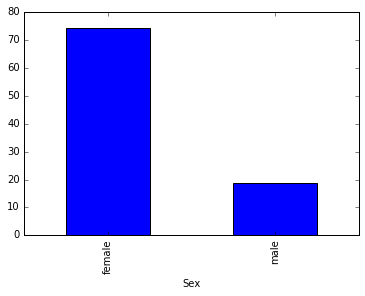
titanic_data_survived_grouped = titanic_data_survived.groupby(['Sex']).Survived.mean()*100
titanic_data_survived_grouped.plot(kind = 'bar')<matplotlib.axes._subplots.AxesSubplot at 0x90d19b0>
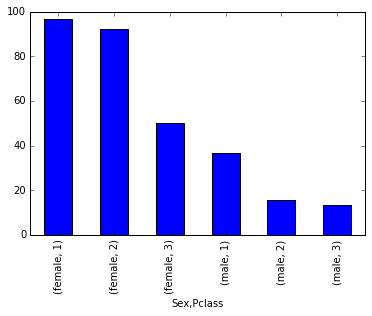
titanic_data_survived = titanic_data
titanic_data_survived_grouped = titanic_data_survived.groupby(['Sex', 'Pclass']).Survived.mean()*100
titanic_data_survived_grouped.plot(kind = 'bar')<matplotlib.axes._subplots.AxesSubplot at 0x9158160>
Based on the raw numbers it would appear as though passengers in Class 3 had a similar survival rate as those from Class 1 with 119 and 136 passengers surviving respectively. However, looking at the percentages of the overall passengers per class and the total numbers across each class, it can be assumed that a passenger from Class 1 is about 2.5x times more likely to survive than a passenger in Class 3.
Social-economic standing was a factor in survival rate of passengers.
- Class 1: 62.96%
- Class 2: 47.28%
- Class 3: 24.24%
Did age, regardless of sex and class, determine your chances of survival?
age_below_18 = len(titanic_data[titanic_data['Age']<18])
print 'Total number of passengers below 18 :',age_below_18
age_below_18_survived = len(titanic_data[titanic_data['Age']<18][titanic_data['Survived']==1])
print 'Total number of passengers below 18 who survived :',age_below_18_survived
print '\n'
age_below_50 = len(titanic_data[titanic_data['Age']>18][titanic_data['Age']<50])
print 'Total number of passengers below 50 :',age_below_50
age_below_50_survived = len(titanic_data[titanic_data['Age']>18][titanic_data['Age']<50][titanic_data['Survived']==1])
print 'Total number of passengers below 50 who survived :',age_below_50_survived
print '\n'
age_above_50 = len(titanic_data[titanic_data['Age']>50])
print 'Total number of passengers above 50 :',age_above_50
age_above_50_survived = len(titanic_data[titanic_data['Age']>50][titanic_data['Survived']==1])
print 'Total number of passengers above 50 who survived :',age_above_50_survived
print '\n'
print 'Below 18 survival rate :',((float(age_below_18_survived)/age_below_18)*100)
print 'Between 18 and 50 survival rate :',((float(age_below_50_survived)/age_below_50)*100)
print 'Above 50 survival rate :',((float(age_above_50_survived)/age_above_50)*100)Total number of passengers below 18 : 113
Total number of passengers below 18 who survived : 61
Total number of passengers below 50 : 501
Total number of passengers below 50 who survived : 193
Total number of passengers above 50 : 64
Total number of passengers above 50 who survived : 22
Below 18 survival rate : 53.98 %
Between 18 and 50 survival rate : 38.52 %
Above 50 survival rate : 34.37 %
print 'Number of missing age values of Male :',missing_age_male.sum()
print 'Number of missing age values of Female :',missing_age_female.sum()Number of missing age values of Male : 124
Number of missing age values of Female : 53
cleaned_age_data = titanic_data.dropna()
total_survivors = cleaned_age_data[cleaned_age_data['Survived']==1]['Age'].count()
total_non_survivors = cleaned_age_data[cleaned_age_data['Survived']==0]['Age'].count()
total_survivors_mean = cleaned_age_data[cleaned_age_data['Survived']==1]['Age'].mean()
total_non_survivors_mean = cleaned_age_data[cleaned_age_data['Survived']==0]['Age'].mean()
print 'Total Survivors : ',total_survivors
print 'Total Non-Survivors :',total_non_survivors
print 'Total Survivors Mean Age:',total_survivors_mean
print 'Total Non-Survivors Mean Age:',total_non_survivors_meanTotal Survivors : 288
Total Non-Survivors : 424
Total Survivors Mean Age: 28.1932986111
Total Non-Survivors Mean Age: 30.6261792453
cleaned_age_data.loc[(cleaned_age_data['Age']<18),'Age_Category'] = 'Young Aged'
cleaned_age_data.loc[(cleaned_age_data['Age']>17) & (cleaned_age_data['Age']<50),'Age_Category'] = 'Middle Aged'
cleaned_age_data.loc[(cleaned_age_data['Age']>50),'Age_Category'] = 'Old Aged'
cleaned_age_data.head()| Survived | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | Age_Category | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | male | 22.0 | 1 | 0 | 7.2500 | S | Middle Aged |
| 1 | 1 | 1 | female | 38.0 | 1 | 0 | 71.2833 | C | Middle Aged |
| 2 | 1 | 3 | female | 26.0 | 0 | 0 | 7.9250 | S | Middle Aged |
| 3 | 1 | 1 | female | 35.0 | 1 | 0 | 53.1000 | S | Middle Aged |
| 4 | 0 | 3 | male | 35.0 | 0 | 0 | 8.0500 | S | Middle Aged |
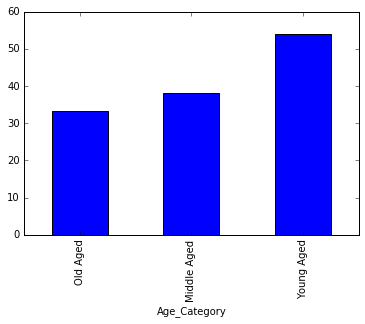
titanic_data_grouped_by_age_category = cleaned_age_data
titanic_data_survival_by_age = (titanic_data_grouped_by_age_category.groupby(['Age_Category']).Survived.mean()*100).sort_values()
titanic_data_survival_by_age.plot(kind = 'bar')<matplotlib.axes._subplots.AxesSubplot at 0x991d9e8>
Based on the above boxplot and calculated data, it would appear that age was a deciding factor in the passenger survival rate but the effect of age was too little and can be considered as insignificant.
Did women and children have preference to lifeboats and therefore survival (assuming there was no shortage of lifeboats)?
Assumption: With "child" not classified in the data, I'll need to assume a cutoff point. Therefore, I'll be using today's standard of under 18 as those to be considered as a child vs adult.
cleaned_age_data.loc[((cleaned_age_data['Sex']=='female') & (cleaned_age_data['Age']>=18)), 'Category'] = 'Woman'
cleaned_age_data.loc[(cleaned_age_data['Sex']=='male') & (cleaned_age_data['Age']>=18), 'Category'] = 'Man'
cleaned_age_data.loc[(cleaned_age_data['Age'] < 18),'Category'] = 'Child'
cleaned_age_data.head()| Survived | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | Age_Category | Category | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | male | 22.0 | 1 | 0 | 7.2500 | S | Middle Aged | Man |
| 1 | 1 | 1 | female | 38.0 | 1 | 0 | 71.2833 | C | Middle Aged | Woman |
| 2 | 1 | 3 | female | 26.0 | 0 | 0 | 7.9250 | S | Middle Aged | Woman |
| 3 | 1 | 1 | female | 35.0 | 1 | 0 | 53.1000 | S | Middle Aged | Woman |
| 4 | 0 | 3 | male | 35.0 | 0 | 0 | 8.0500 | S | Middle Aged | Man |
print cleaned_age_data.groupby(['Category', 'Survived']).size()Category Survived
Child 0 52
1 61
Man 0 325
1 70
Woman 0 47
1 157
dtype: int64
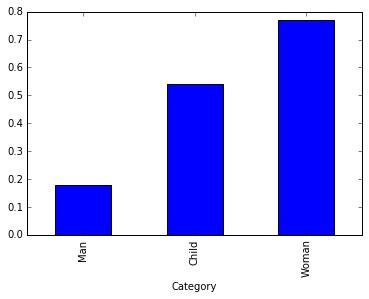
cleaned_age_grouped_by_category = cleaned_age_data.groupby('Category')
cleaned_age_grouped_by_category_survival = cleaned_age_grouped_by_category.Survived.mean().sort_values()
cleaned_age_grouped_by_category_survival.plot(kind = 'bar')<matplotlib.axes._subplots.AxesSubplot at 0x9cb6a20>
The data, and more so, the graphs tends to support the idea that "women and children first" possibly played a role in the survival of a number of people. It's a bit surprising that more children didn't survive but this could possibly be attributed to the mis-representation of what age is considered as the cut off for adults - i.e. if in the 1900's someone 15-17 were considered adults, they would not have been "saved" under the "women and children first" idea and would be made to fend for themselves. That would in turn, change the outcome of the above data and possible increase the number of children who survived.
How did children with nannies fare in comparison to children with parents. Did the nanny "abandon" children to save his/her own life?
- Need to review list for children with no parents. These will be children with nannies as stated in the data description
- Compare "normal" survival rate of children with parents against children with nannies
Assumptions:
-
If you're classified as a 'Child' (under 18) and have Parch > 0, then the value is associated to your Parents, eventhough it is possible to be under 18 and also have children
-
Classifying people as 'Child' represented by those under 18 years old is applying today's standards to the 1900 century
children_with_nanny = cleaned_age_data[cleaned_age_data['Category']=='Child'][cleaned_age_data['Parch']==0]
children_with_parents = cleaned_age_data[cleaned_age_data['Category']=='Child'][cleaned_age_data['Parch'] > 0]
print 'Number of childern with nanny:',children_with_nanny['Survived'].count()
print 'Number of childern with nanny who survived:',children_with_nanny[children_with_nanny['Survived']==1]['Survived'].count()
print 'Number of childern with nanny:',children_with_parents['Survived'].count()
print 'Number of childern with nanny who survived:',\
children_with_parents[children_with_parents['Survived']==1]['Survived'].count()Number of childern with nanny: 32
Number of childern with nanny who survived: 16
Number of childern with nanny: 81
Number of childern with nanny who survived: 45
print 'Percentage of children who survived with nanny:',\
(float(children_with_nanny[children_with_nanny['Survived']==1]['Survived'].count())/children_with_nanny['Survived'].count())*100
print 'Mean age of children who survived with nanny:',\
children_with_nanny[children_with_nanny['Survived']==1]['Age'].mean()Percentage of children who survived with nanny: 50.0
Mean age of children who survived with nanny: 14.6875
print 'Percentage of children who survived with parents:',\
(float(children_with_parents[children_with_parents['Survived']==1]['Survived'].count())/\
children_with_parents['Survived'].count())*100
print 'Mean age of children who survived with parents:',\
children_with_parents[children_with_parents['Survived']==1]['Age'].mean()Percentage of children who survived with parents: 55.5555555556
Mean age of children who survived with parents: 5.47044444444
cleaned_age_data.loc[((cleaned_age_data['Parch']==0) & (cleaned_age_data['Category']=='Child')), 'nanny_parents'] = 'With_nanny'
cleaned_age_data.loc[((cleaned_age_data['Parch']>0) & (cleaned_age_data['Category']=='Child')),'nanny_parents']='Without_nanny'
cleaned_age_data.head()| Survived | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | Age_Category | Category | nanny_parents | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | male | 22.0 | 1 | 0 | 7.2500 | S | Middle Aged | Man | NaN |
| 1 | 1 | 1 | female | 38.0 | 1 | 0 | 71.2833 | C | Middle Aged | Woman | NaN |
| 2 | 1 | 3 | female | 26.0 | 0 | 0 | 7.9250 | S | Middle Aged | Woman | NaN |
| 3 | 1 | 1 | female | 35.0 | 1 | 0 | 53.1000 | S | Middle Aged | Woman | NaN |
| 4 | 0 | 3 | male | 35.0 | 0 | 0 | 8.0500 | S | Middle Aged | Man | NaN |
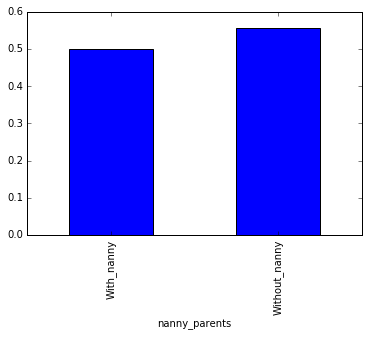
cleaned_age_data_nanny_group = cleaned_age_data.groupby('nanny_parents').Survived.mean()
cleaned_age_data_nanny_group.plot(kind = 'bar')<matplotlib.axes._subplots.AxesSubplot at 0x9f34cf8>
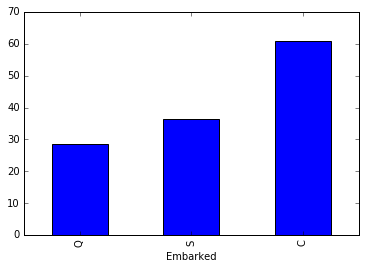
data_embarked_group = (cleaned_age_data.groupby('Embarked').Survived.mean()*100).sort_values()
data_embarked_group.plot(kind = 'bar')<matplotlib.axes._subplots.AxesSubplot at 0xa0329e8>
Based on the data analysis above, it would appear that the survival rate for children who were accompanied by parents vs those children accompanied by nannies was slighly higher for those with parents. The slight increase could be due to the average age of children with parents being younger, almost half, that of children with nannies.
- Percentage of children with nannies who survived: 50.0%
- Percentage of children with parents who survived: 55.56%
- Average age of surviving children with nannies: 15
- Average age of surviving children with parents: 7.0
The results of the analysis, although tentative, would appear to indicate that class and sex, namely, being a female with upper social-economic standing (first class), would give one the best chance of survival when the tragedy occurred on the Titanic. Age did not seem to be a major factor. While being a man in third class, gave one the lowest chance of survival. Women and children, across all classes, tend to have a higher survival rate than men in general but by no means did being a child or woman guarentee survival. Although, overall, children accompanied by parents (or nannies) had the best survival rate at over 50%.
- A portion of men and women did not have Age data and were removed from calculations which could have skewed some numbers.
- The category of 'children' was assumed to be anyone under the age of 18, using today's North American standard for adulthood which was certainly not the case in the 1900s.