Autodiff is a numerical optimization and linear algebra library for the Go / Golang programming language. It implements basic automatic differentation for many mathematical routines. The documentation of this package can be found here.
Autodiff has two different scalar types. The Real type allows to store first and second derivatives for the current value, whereas the BareReal type is a simple float64 which cannot store any information other than its value. Every scalar supports the following set of functions:
| Function | Description |
|---|---|
| Min | Minimum |
| Max | Maximum |
| Abs | Absolute value |
| Sign | Sign |
| Neg | Negation |
| Add | Addition |
| Sub | Substraction |
| Mul | Multiplication |
| Div | Division |
| Pow | Power |
| Sqrt | Square root |
| Exp | Exponential function |
| Log | Logarithm |
| Log1p | Logarithm of 1+x |
| Log1pExp | Logarithm of 1+Exp(x) |
| Logistic | Standard logistic function |
| Erf | Error function |
| Erfc | Complementary error function |
| LogErfc | Log complementary error function |
| Sigmoid | Numerically stable sigmoid function |
| Sin | Sine |
| Sinh | Hyperbolic sine |
| Cos | Cosine |
| Cosh | Hyperbolic cosine |
| Tan | Tangent |
| Tanh | Hyperbolic tangent |
| LogAdd | Addition on log scale |
| LogSub | Substraction on log scale |
| SmoothMax | Differentiable maximum |
| LogSmoothMax | Differentiable maximum on log scale |
| Gamma | Gamma function |
| Lgamma | Log gamma function |
| Mlgamma | Multivariate log gamma function |
| GammaP | Lower incomplete gamma function |
| BesselI | Modified Bessel function of the first kind |
| LogBesselI | Log of the Modified Bessel function of the first kind |
Autodiff supports vectors and matrices including basic linear algebra operations. Vectors support the following linear algebra operations:
| Function | Description |
|---|---|
| VaddV | Element-wise addition |
| VsubV | Element-wise substraction |
| VmulV | Element-wise multiplication |
| VdivV | Element-wise division |
| VaddS | Addition of a scalar |
| VsubS | Substraction of a scalar |
| VmulS | Multiplication with a scalar |
| VdivS | Division by a scalar |
| VdotV | Dot product |
Matrices support the following linear algebra operations:
| Function | Description |
|---|---|
| MaddM | Element-wise addition |
| MsubM | Element-wise substraction |
| MmulM | Element-wise multiplication |
| MdivM | Element-wise division |
| MaddS | Addition of a scalar |
| MsubS | Substraction of a scalar |
| MmulS | Multiplication with a scalar |
| MdivS | Division by a scalar |
| MdotM | Matrix product |
| Outer | Outer product |
The algorithms package contains more complex linear algebra and optimization routines:
| Package | Description |
|---|---|
| bfgs | Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm |
| blahut | Blahut algorithm (channel capacity) |
| cholesky | Cholesky and LDL factorization |
| determinant | Matrix determinants |
| eigensystem | Compute Eigenvalues and Eigenvectors |
| gaussJordan | Gauss-Jordan algorithm |
| gradientDescent | Vanilla gradient desent algorithm |
| gramSchmidt | Gram-Schmidt algorithm |
| hessenbergReduction | Matrix Hessenberg reduction |
| lineSearch | Line-search (satisfying the Wolfe conditions) |
| matrixInverse | Matrix inverse |
| msqrt | Matrix square root |
| msqrtInv | Inverse matrix square root |
| newton | Newton's method (root finding and optimization) |
| qrAlgorithm | QR-Algorithm for computing Schur decompositions |
| rprop | Resilient backpropagation |
| svd | Singular Value Decomposition (SVD) |
| saga | SAGA stochastic average gradient descent method |
Import the autodiff library with
import . "github.com/pbenner/autodiff"A scalar holding the value 1.0 can be defined in several ways, i.e.
a := NewScalar(RealType, 1.0)
b := NewReal(1.0)
c := NewBareReal(1.0)a and b are both Reals, however a has type Scalar whereas b has type *Real which implements a Scalar. Variable c is of type *BareReal which cannot carry any derivatives. Basic operations such as additions are defined on all Scalars, i.e.
a.Add(a, b)which stores the result of adding a and b in a. If autodiff/simple is imported, one may also use
d := Add(a, b)where the result is stored in a new variable d. The ConstReal type allows to define real constants without allocation of additional memory. For instance
a.Add(a, ConstReal(1.0))adds a constant value to a where a type cast is used to define the constant 1.0.
To differentiate a function
f := func(x, y Scalar) Scalar {
return Add(Mul(x, Pow(y, NewReal(3))), NewReal(4))
}first two reals are defined
x := NewReal(2)
y := NewReal(4)that store the value at which the derivative of f should be evaluated. Afterwards, x and y must be defined as variables with
Variables(2, x, y)where the first argument says that derivatives up to second order should be computed. After evaluating f, i.e.
z := f(x, y)the function value at (x,y) = (2, 4) can be retrieved with z.GetValue(). The first and second partial derivatives can be accessed with z.GetDerivative(i) and z.GetHessian(i, j), where the arguments specify the index of the variable. For instance, the derivative of f with respect to x is returned by z.GetDerivative(0), whereas the derivative with respect to y by z.GetDerivative(1).
Vectors and matrices can be created with
v := NewVector(RealType, []float64{1,2})
m := NewMatrix(RealType, 2, 2, []float64{1,2,3,4})where v has length 2 and m is a 2x2 matrix. With
v := NullVector(RealType, 2)
m := NullMatrix(RealType, 2, 2)all values are initially set to zero. Vector and matrix elements can be accessed with the At method, which returns a reference to the Scalar, i.e.
m.At(1,1).Add(v.At(0), v.At(1))adds the first two values in v and stores the result in the lower right element of the matrix m. Autodiff supports basic linear algebra operations, for instance, the vector matrix product can be computed with
w := NullVector(RealType, 2)
w.MdotV(m, v)where the result is stored in w. Other operations, such as computing the eigenvalues and eigenvectors of a matrix, require importing the respective package from the algorithm library, i.e.
import "github.com/pbenner/autodiff/algorithm/eigensystem"
lambda, _, _ := eigensystem.Run(m)Compare vanilla gradient descent with resilient backpropagation
import . "github.com/pbenner/autodiff"
import "github.com/pbenner/autodiff/algorithm/gradientDescent"
import "github.com/pbenner/autodiff/algorithm/rprop"
import . "github.com/pbenner/autodiff/simple"
f := func(x Vector) Scalar {
// x^4 - 3x^3 + 2
return Add(Sub(Pow(x.At(0), NewReal(4)), Mul(NewReal(3), Pow(x.At(0), NewReal(3)))), NewReal(2))
}
x0 := NewVector(RealType, []float64{8})
// vanilla gradient descent
xn1, _ := gradientDescent.Run(f, x0, 0.0001, gradientDescent.Epsilon{1e-8})
// resilient backpropagation
xn2, _ := rprop.Run(f, x0, 0.0001, 0.4, rprop.Epsilon{1e-8})Compute the inverse r of a matrix m by minimizing the Frobenius norm ||mb - I||
import . "github.com/pbenner/autodiff"
import "github.com/pbenner/autodiff/algorithm/rprop"
import . "github.com/pbenner/autodiff/simple"
m := NewMatrix(RealType, 2, 2, []float64{1,2,3,4})
I := IdentityMatrix(RealType, 2)
r := m.Clone()
// objective function
f := func(x Vector) Scalar {
r.SetValues(x)
s := Mnorm(MsubM(MmulM(m, r), I))
return s
}
x, _ := rprop.Run(f, r.GetValues(), 0.01, 0.1, rprop.Epsilon{1e-12})
r.SetValues(x)Find the root of a function f with initial value x0 = (1,1)
import . "github.com/pbenner/autodiff"
import "github.com/pbenner/autodiff/algorithm/newton"
import . "github.com/pbenner/autodiff/simple"
f := func(x Vector) Vector {
y := NilVector(2)
// y1 = x1^2 + x2^2 - 6
// y2 = x1^3 - x2^2
y.At(0).Sub(Add(Pow(x.At(0), NewReal(2)), Pow(x.At(1), NewReal(2))), NewReal(6))
y.At(1).Sub(Pow(x.At(0), NewReal(3)), Pow(x.At(1), NewReal(2)))
return y
}
x0 := NewVector(RealType, []float64{1,1})
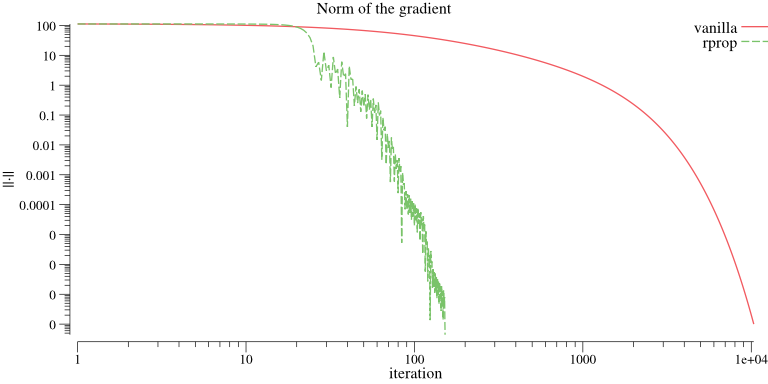
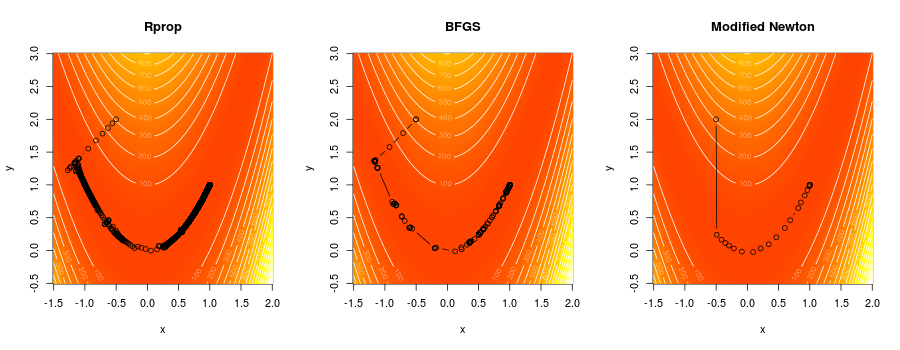
xn, _ := newton.RunRoot(f, x0, newton.Epsilon{1e-8})Compare Newton's method, BFGS and Rprop for minimizing Rosenbrock's function
import . "github.com/pbenner/autodiff"
import "github.com/pbenner/autodiff/algorithm/rprop"
import "github.com/pbenner/autodiff/algorithm/bfgs"
import "github.com/pbenner/autodiff/algorithm/newton"
import . "github.com/pbenner/autodiff/simple"
f := func(x Vector) (Scalar, error) {
// f(x1, x2) = (a - x1)^2 + b(x2 - x1^2)^2
// a = 1
// b = 100
// minimum: (x1,x2) = (a, a^2)
a := NewReal( 1.0)
b := NewReal(100.0)
s := Pow(Sub(a, x.At(0)), NewReal(2.0))
t := Mul(b, Pow(Sub(x.At(1), Mul(x.At(0), x.At(0))), NewReal(2.0)))
return Add(s, t), nil
}
hook_bfgs := func(x, gradient Vector, y Scalar) bool {
fmt.Println("x :", x)
fmt.Println("gradient:", gradient)
fmt.Println("y :", y)
fmt.Println()
return false
}
hook_rprop := func(gradient, step []float64, x Vector, y Scalar) bool {
fmt.Println("x :", x)
fmt.Println("gradient:", gradient)
fmt.Println("y :", y)
fmt.Println()
return false
}
hook_newton := func(x, gradient Vector, hessian Matrix, y Scalar) bool {
fmt.Println("x :", x)
fmt.Println("gradient:", gradient)
fmt.Println("y :", y)
fmt.Println()
return false
}
x0 := NewVector(RealType, []float64{-0.5, 2})
rprop.Run(f, x0, 0.05, []float64{1.2, 0.8},
rprop.Hook{hook_rprop},
rprop.Epsilon{1e-10})
bfgs.Run(f, x0,
bfgs.Hook{hook_bfgs},
bfgs.Epsilon{1e-10})
newton.RunMin(f, x0,
newton.HookMin{hook_newton},
newton.Epsilon{1e-8},
newton.HessianModification{"LDL"})Maximize the function f(x, y) = x + y subject to x^2 + y^2 = 1 by finding the critical point of the corresponding Lagrangian
import . "github.com/pbenner/autodiff"
import "github.com/pbenner/autodiff/algorithm/newton"
import . "github.com/pbenner/autodiff/simple"
// define the Lagrangian
f := func(x Vector) (Scalar, error) {
// x + y + lambda(x^2 + y^2 - 1)
y := Add(Add(x.At(0), x.At(1)), Mul(x.At(2), Sub(Add(Mul(x.At(0), x.At(0)), Mul(x.At(1), x.At(1))), NewReal(1))))
return y, nil
}
// initial value
x0 := NewVector(RealType, []float64{3, 5, 1})
// run Newton's method
xn, _ := newton.RunCrit(
f, x0,
newton.Epsilon{1e-8})