腾讯&字节等：最小的k个数

[sisterAn]

话不多说，来一道题目加深一下理解吧：

输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

 示例 1：

输入：arr = [3,2,1], k = 2
输出：[1,2] 或者 [2,1]

示例 2：

输入：arr = [0,1,2,1], k = 1
输出：[0]

限制：

• 0 <= k <= arr.length <= 10000
• 0 <= arr[i] <= 10000

附赠leetcode地址：leetcode

[Malenconiaprincep]

1. js api

var newsort = arr.sort((a, b) => a - b)
return newsort.slice(0, k)

2. 快排

function quicksort(arr) {
    if(arr.length <= 1) return arr
    var pivotIndex = Math.floor(arr.length / 2)
    var pivot = arr.splice(pivotIndex, 1)[0];
    var left = []
    var right = []
    for(let i=0; i < arr.length; i++) {
        if(arr[i] < pivot) {
            left.push(arr[i])
        } else {
            right.push(arr[i])
        }
    }
   return quicksort(left).concat(pivot, quicksort(right))
}

[plane-hjh]

简单粗暴

排序+ slice

先把输入的 n 个数排序，排序之后位于前面的 k 个数就是最小的 k 个数。

/**
 * @param {number[]} arr
 * @param {number} k
 * @return {number[]}
 */
const getLeastNumbers = function(arr, k) {
    arr.sort((a, b) => a - b)

    return arr.slice(0, k)
};

但是这样的时间复杂度是 O(nlogn)，并不是我们想要的

快排

快排的 关键 在于先在数组中选择一个数字，接下来把数组中的数字分为两部分，比选择的数字小的数字移到数组的左边，比选择的数字大的数字移到数组的右边。这个函数可以这样实现

function partition (arr, low, high) {
    let x = arr[high];
    let i = low - 1;
    for(let j = low; j < high; j++) {
        if(arr[j] <= x){
            i++;
            [arr[i], arr[j]] = [arr[j], arr[i]]
        }
    }
    [arr[i+1], arr[high]] = [arr[high], arr[i+1]]
    return i + 1;
}

比第 k 个数字小的所有数组都位于数组的左边，比第 k 个数字大的都位于右边

/**
 * @param {number[]} arr
 * @param {number} k
 * @return {number[]}
 */
const getLeastNumbers = function(arr, k) {
    const length = arr.length;
    if (k >= length) return arr;
    let left = 0,
        right = length - 1;
    let index = partition(arr, left, right);
    while (index !== k) {
        if (index < k) {
            left = index + 1;
            index = partition(arr, left, right);
        } else if (index > k) {
            right = index - 1;
            index = partition(arr, left, right);
        }
    }

    return arr.slice(0, k);
};

时间复杂度为 O(n) , 缺点是会修改到输入的数字

备注：看了一早上这种方法的实现，脑子不够用了。附本人觉得的优秀答案解答

[0undefined0]

排序加获取

function quicksort(arr) {
  if (arr.length <= 1) return arr;
  const pivotIndex = Math.floor(arr.length / 2);
  const pivot = arr.splice(pivotIndex, 1)[0];
  const left = [];
  const right = [];
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return quicksort(left).concat(pivot, quicksort(right));
}
function findK(arr, k) {
 return quicksort(arr).slice(0, k);
}

[sisterAn]

这是一道典型的 Top k 问题

所谓 Top k 问题？简单来说就是在一组数据里面找到频率出现最高的前 k 个数，或前 k 大（当然也可以是前 k 小）的数。

这种问题我们该怎么处理喃？

最简单的就是将数组进行排序（可以是最简单的快排），取前 K 个数就可以了，so easy

解答一：数组排序，取前 k 个数

代码实现：

let getLeastNumbers = function(arr, k) {
    return arr.sort((a, b) => a - b).slice(0, k);
}

复杂度分析：

• 时间复杂度：O(nlogn)
• 空间复杂度：O(logn)

注意：

在 V8 引擎 7.0 版本之前，数组长度小于10时， Array.prototype.sort() 使用的是插入排序，否则用快速排序。

在 V8 引擎 7.0 版本之后就舍弃了快速排序，因为它不是稳定的排序算法，在最坏情况下，时间复杂度会降级到 O(n²)。

而是采用了一种混合排序的算法：TimSort 。

这种功能算法最初用于Python语言中，严格地说它不属于以上10种排序算法中的任何一种，属于一种混合排序算法：

在数据量小的子数组中使用插入排序，然后再使用归并排序将有序的子数组进行合并排序，时间复杂度为 O(nlogn) 。

解法二：构建大顶堆求 Top k问题

我们也可以通过构造一个大顶堆来解决，大顶堆上的任意节点值都必须大于等于其左右子节点值，即堆顶是最大值。

所以我们可以重数组中取出 k 个元素构造一个大顶堆，然后将其余元素与大顶堆对比，如果小于堆顶则替换堆顶，然后堆化，所有元素遍历完成后，堆中的元素即为前 k 个最小值

具体步骤如下：

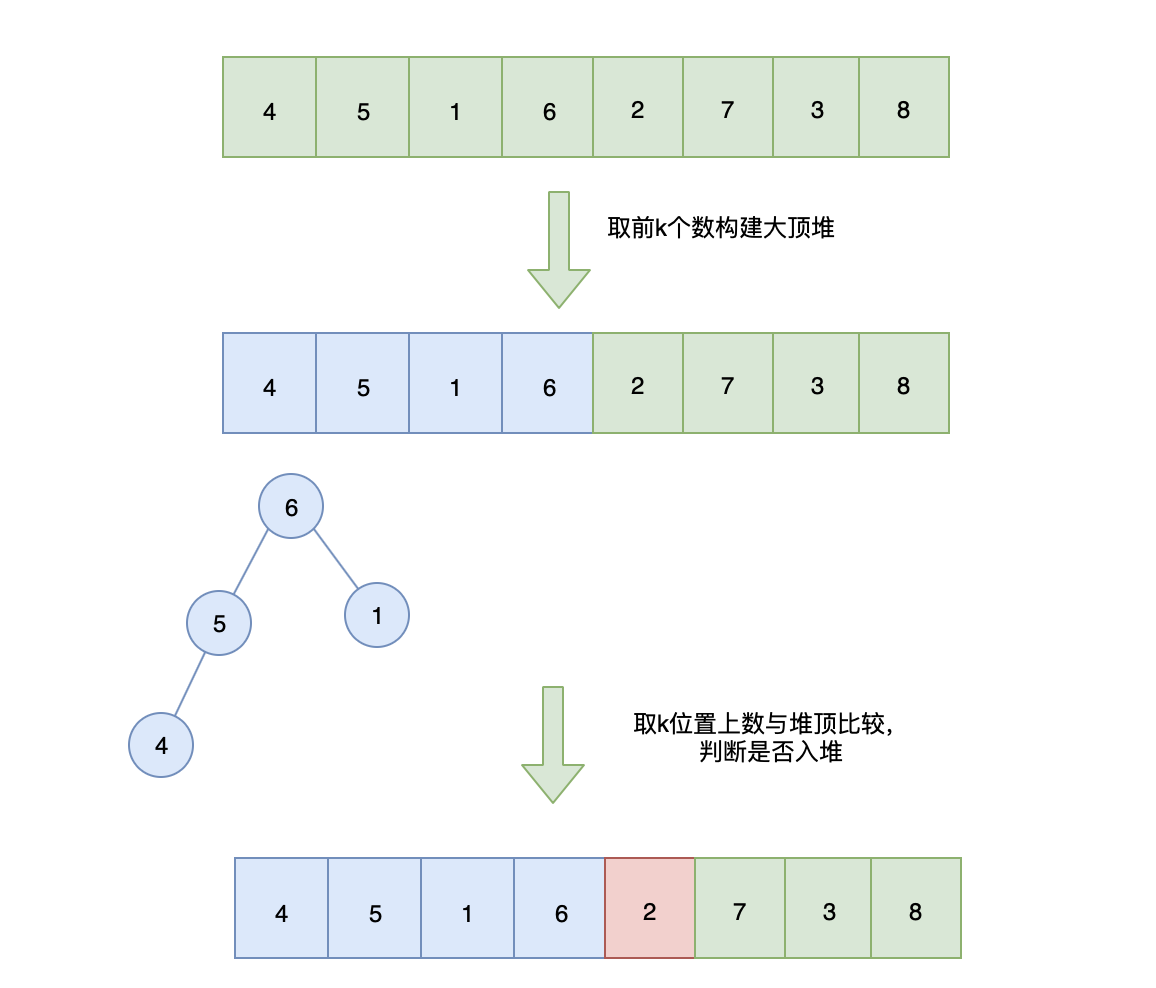
• 从数组中取前 k 个数（ 0 到 k-1 位），构造一个大顶堆
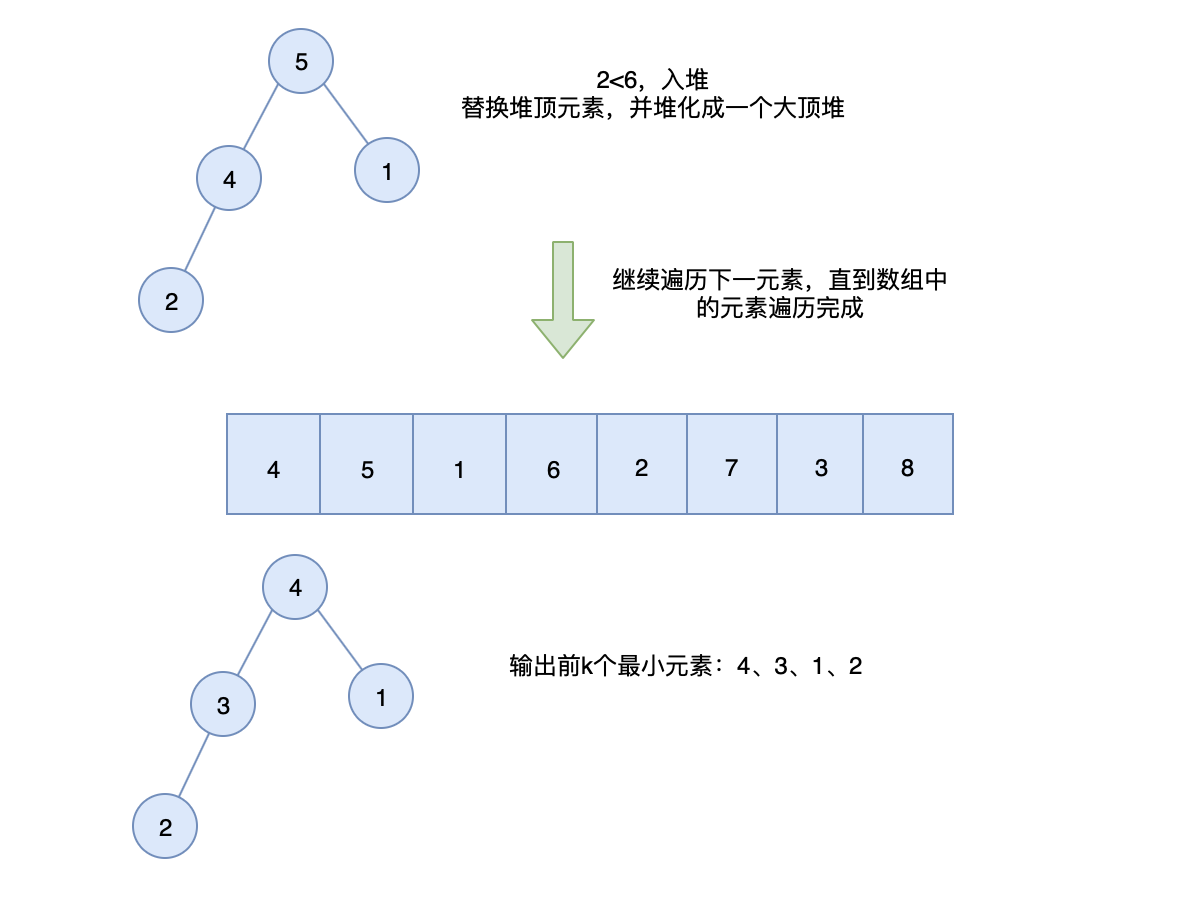
• 从 k 位开始遍历数组，每一个数据都和大顶堆的堆顶元素进行比较，如果大于堆顶元素，则不做任何处理，继续遍历下一元素；如果小于堆顶元素，则将这个元素替换掉堆顶元素，然后再堆化成一个大顶堆。
• 遍历完成后，堆中的数据就是前 K 小的数据

代码实现：

let getLeastNumbers = function(arr, k) {
    // 从 arr 中取出前 k 个数，构建一个大顶堆
    let heap = [,], i = 0
    while(i < k) {
       heap.push(arr[i++]) 
    }
    buildHeap(heap, k)
    
    // 从 k 位开始遍历数组
    for(let i = k; i < arr.length; i++) {
        if(heap[1] > arr[i]) {
            // 替换并堆化
            heap[1] = arr[i]
            heapify(heap, k, 1)
        }
    }
    
    // 删除heap中第一个元素
    heap.shift()
    return heap
};

// 原地建堆，从后往前，自上而下式建大顶堆
let buildHeap = (arr, k) => {
    if(k === 1) return
    // 从最后一个非叶子节点开始，自上而下式堆化
    for(let i = Math.floor(k/2); i>=1 ; i--) {
        heapify(arr, k, i)
    }
}

// 堆化
let heapify = (arr, k, i) => {
    // 自上而下式堆化
    while(true) {
        let maxIndex = i
        if(2*i <= k && arr[2*i] > arr[i]) {
            maxIndex = 2*i
        }
        if(2*i+1 <= k && arr[2*i+1] > arr[maxIndex]) {
            maxIndex = 2*i+1
        }
        if(maxIndex !== i) {
            swap(arr, i, maxIndex)
            i = maxIndex
        } else {
            break
        }
    }
}

// 交换
let swap = (arr, i , j) => {
    let temp = arr[i]
    arr[i] = arr[j]
    arr[j] = temp
}

复杂度分析：

• 时间复杂度：遍历数组需要 O(n) 的时间复杂度，一次堆化需要 O(logk) 时间复杂度，所以利用堆求 Top k 问题的时间复杂度为 O(nlogk)
• 空间复杂度：O(k)

利用堆求 Top k 问题的优势

这种求 Top k 问题是可以使用排序来处理，但当我们需要在一个动态数组中求 Top k 元素怎么办喃？

动态数组可能会插入或删除元素，难道我们每次求 Top k 问题的时候都需要对数组进行重新排序吗？那每次的时间复杂度都为 O(nlogn)

这里就可以使用堆，我们可以维护一个 K 大小的小顶堆，当有数据被添加到数组中时，就将它与堆顶元素比较，如果比堆顶元素大，则将这个元素替换掉堆顶元素，然后再堆化成一个小顶堆；如果比堆顶元素小，则不做处理。这样，每次求 Top k 问题的时间复杂度仅为 O(logk)

更多堆内容可查看 前端进阶算法9：看完这篇，再也不怕堆排序、Top K、中位数问题面试了

解法三：计数排序

计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。

作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。它是一种典型的拿空间换时间的排序算法

代码实现：

let getLeastNumbers = function(arr, k) {
    return countingSort(arr, 10000, k)
}

let countingSort = (arr, maxValue, k) => {
    // 开辟的新的数组，用于将输入的数据值转化为键存储
    var bucket = new Array(maxValue + 1),
        sortedIndex = 0,
        arrLen = arr.length,
        bucketLen = maxValue + 1

    // 存储
    for (var i = 0; i < arrLen; i++) {
        if (!bucket[arr[i]]) {
            bucket[arr[i]] = 0
        }
        bucket[arr[i]]++
    }

    // 将数据从bucket按顺序写入res中，控制仅仅输出前k个
    let res = []
    for (var j = 0; j < bucketLen; j++) {
        while(bucket[j]-- > 0 && sortedIndex < k) {
            res[sortedIndex++] = j
        }
        if(sortedIndex === k) {
            break
        }
    }
    return res
}

复杂度分析：

• 时间复杂度：O(n + m)，其中 m 表示数据范围
• 空间复杂度：O(k + m)
  同时V8也对数组提供了slow、fast存储，一定程度上提高了计数排序的性能，具体可查看 前端进阶算法2：从Chrome V8源码看JavaScript数组（附赠腾讯面试题）

leetcode

[XW666]

//使用冒泡排序

const countingSort = (arr, k) => {
for (let i = 0; i < arr.length; i++) {
for (let j = i + 1; j < arr.length; j++) {

    if (arr[i] > arr[j]) {
      let val = arr[i];
      arr[i] = arr[j];
      arr[j] = val
    }
  }
}
return arr.slice(0, k)

}

[AAAngelina]

借鉴快排的**
`var smallestK = function (arr, k) {
sort(arr, 0, arr.length - 1, k);
return arr.slice(0, k);
}

function sort(arr, l, r, k) {
if (l >= r) return;
let pos = quicksort(arr, l, r);
let n = pos - l + 1;
if (n === k) {
return;
} else if (n < k) {
sort(arr, pos + 1, r, k - n)
} else if (n > k) {
sort(arr, l, pos - 1, k)
}
}

function quicksort(arr, l, r) {
let baseval = arr[l], index = l;
while (l < r) {
while (l < r && arr[l] <= baseval) l++;
while (l < r && arr[r] > baseval) r--;
if (l < r) {
[arr[l], arr[r]] = [arr[r], arr[l]];
l++;
r--;
}
}
[arr[index], arr[l]] = [arr[l], arr[index]];
return l;
}`

[Jet12138]

/**

• @param {number[]} arr

• @param {number} k

• @return {number[]}
  */
  function swap(arr, i , j){
  let temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
  }
  // 堆化
  function heapify(arr, n, i){
  // n 代表这颗树里面有n个节点。
  // i 代表要对第i个节点做堆化操作
  // 自上而下式堆化

  if(i>=n){
  return ;
  }
  let maxindex = i;
  let c1 = 2i+1; //左子节点的值对应arr中的索引
  let c2 = 2i+2; //右子节点的值对应arr中的索引

  if(c1<n && arr[c1]>arr[i]){
  maxindex = c1;
  }
  if(c2<n && arr[c2]>arr[maxindex]){
  maxindex = c2;
  }
  if(maxindex !== i){
  swap(arr, maxindex, i);

   heapify(arr, n, maxindex);
  

  }

}

// 原地建堆，从后往前，自上而下式建大顶堆(顶元素是堆中最大的。)
function build_heap(arr, n){
let lastnode = n-1; // 堆数组的最后一个值的索引
let lastparent = Math.floor((lastnode-1)/2);

// 从最后一个非叶子节点开始，自上而下式堆化
for(let i = lastparent; i>=0; i--){
    heapify(arr, n, i);
}

}
var getLeastNumbers = function(arr, k) {
let heap = [];
// 从 arr 中取出前 k 个数，构建一个大顶堆
for(let i=0; i<k; i++){
heap.push(arr[i]);
}
build_heap(heap, k);

for(let i= k; i<arr.length; i++){
if(arr[i]<heap[0]){
// 替换堆顶元素并堆化（自顶而下）
heap[0] = arr[i];
heapify(heap, k, 0);
}
}

return heap;
};