前端进阶算法9:看完这篇,再也不怕堆排序、Top K、中位数问题面试了
sisterAn opened this issue · 10 comments
引言
堆是前端进阶必不可少的知识,也是面试的重难点,例如内存堆与垃圾回收、Top K 问题等,这篇文章将从基础开始梳理整个堆体系,按以下步骤来讲:
- 什么是堆
- 怎样建堆
- 堆排序
- 内存堆与垃圾回收
- Top K 问题
- 中位数问题
- 最后来一道leetcode题目,加深理解
下面开始吧👇
一、堆
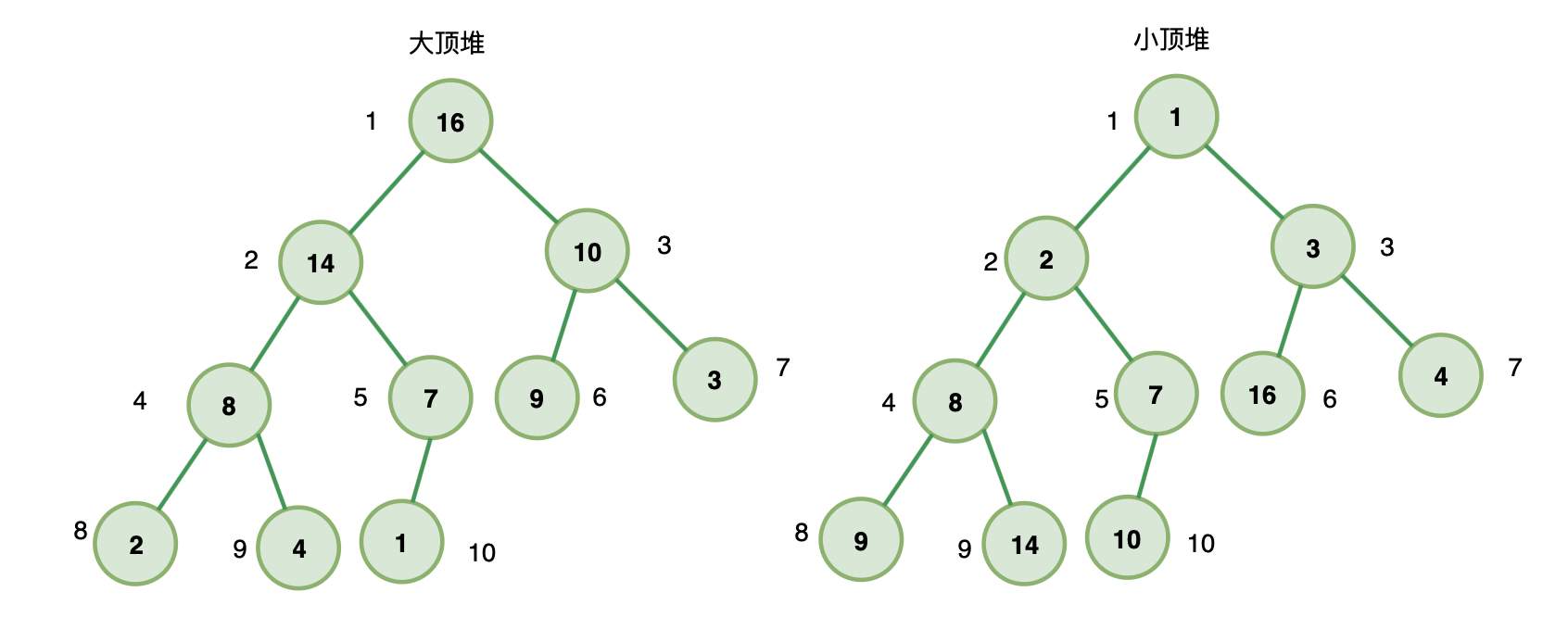
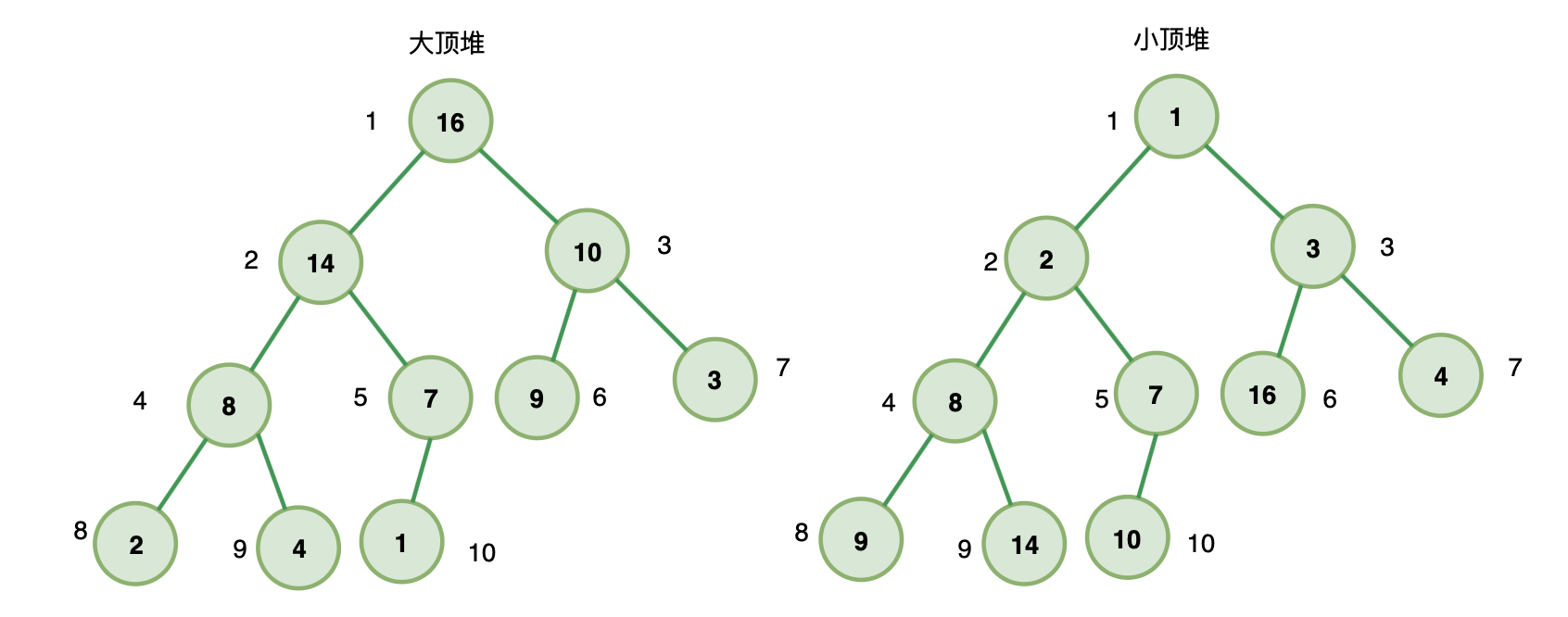
满足下面两个条件的就是堆:
- 堆是一个完全二叉树
- 堆上的任意节点值都必须大于等于(大顶堆)或小于等于(小顶堆)其左右子节点值
如果堆上的任意节点都大于等于子节点值,则称为 大顶堆
如果堆上的任意节点都小于等于子节点值,则称为 小顶堆
也就是说,在大顶堆中,根节点是堆中最大的元素;
在小顶堆中,根节点是堆中最小的元素;
二、怎样创建一个大(小)顶堆
我们在上一节说过,完全二叉树适用于数组存储法( 前端进阶算法7:小白都可以看懂的树与二叉树 ),而堆又是一个完全二叉树,所以它可以直接使用数组存储法存储:
简单来说: 堆其实可以用一个数组表示,给定一个节点的下标 i (i从1开始) ,那么它的父节点一定为 A[i/2] ,左子节点为 A[2i] ,右子节点为 A[2i+1]
function Heap() {
let items = [,]
}那么怎样去创建一个大顶堆(小顶堆)喃?
常用的方式有两种:
- 插入式创建:每次插入一个节点,实现一个大顶堆(或小顶堆)
- 原地创建:又称堆化,给定一组节点,实现一个大顶堆(或小顶堆)
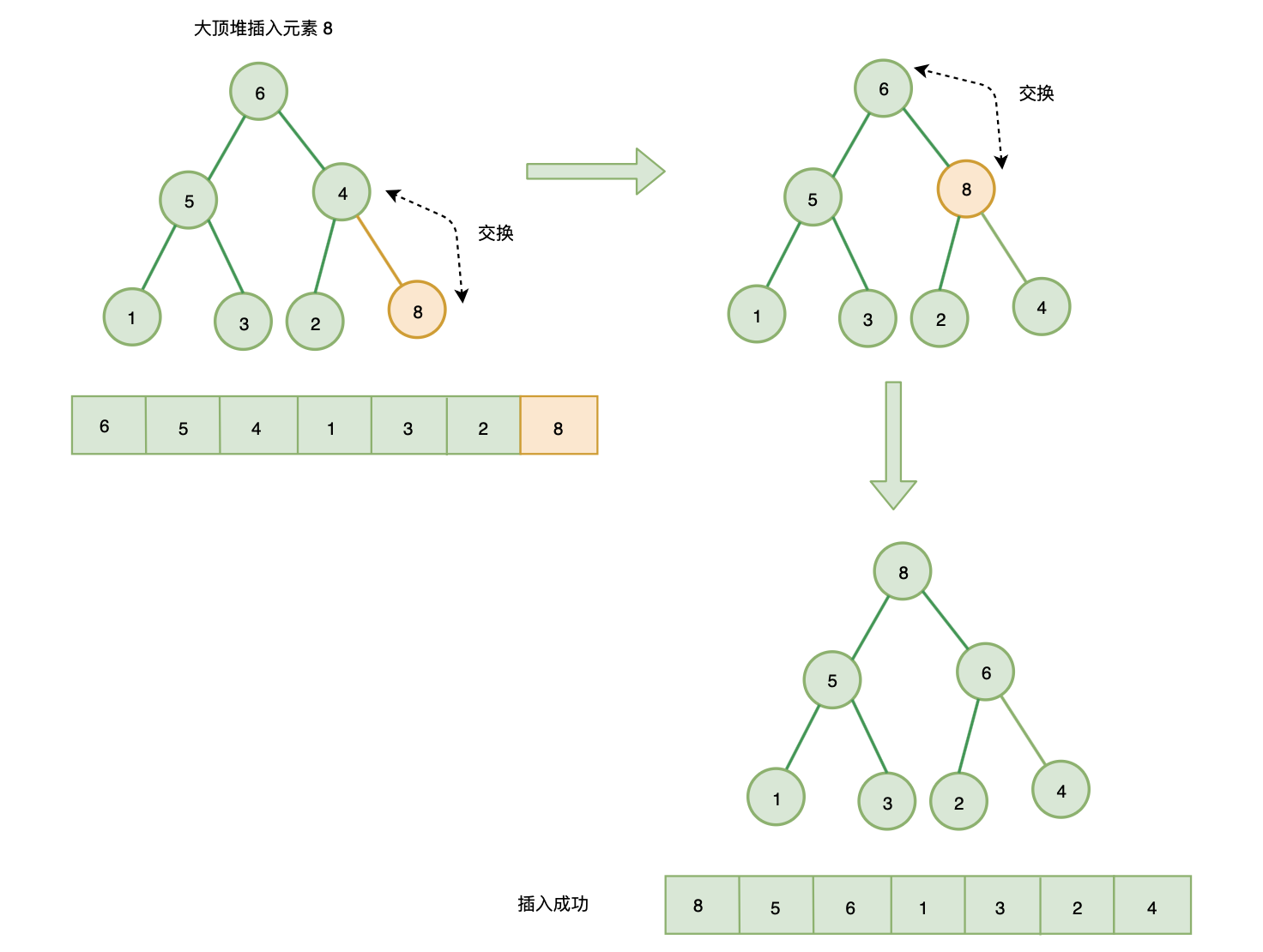
三、插入式建堆
插入节点:
- 将节点插入到队尾
- 自下往上堆化: 将插入节点与其父节点比较,如果插入节点大于父节点(大顶堆)或插入节点小于父节点(小顶堆),则插入节点与父节点调整位置
- 一直重复上一步,直到不需要交换或交换到根节点,此时插入完成。
代码实现:
function insert(key) {
items.push(key)
// 获取存储位置
let i = items.length-1
while (i/2 > 0 && items[i] > items[i/2]) {
swap(items, i, i/2); // 交换
i = i/2;
}
}
function swap(items, i, j) {
let temp = items[i]
items[i] = items[j]
items[j] = temp
}时间复杂度: O(logn),为树的高度
四、原地建堆(堆化)
假设一组序列:
let arr = [,1, 9, 2, 8, 3, 7, 4, 6, 5]原地建堆的方法有两种:一种是承袭上面插入的**,即从前往后、自下而上式堆化建堆;与之对应的另一种是,从后往前、自上往下式堆化建堆。其中
- 自下而上式堆化 :将节点与其父节点比较,如果节点大于父节点(大顶堆)或节点小于父节点(小顶堆),则节点与父节点调整位置
- 自上往下式堆化 :将节点与其左右子节点比较,如果存在左右子节点大于该节点(大顶堆)或小于该节点(小顶堆),则将子节点的最大值(大顶堆)或最小值(小顶堆)与之交换
所以,自下而上式堆是调整节点与父节点(往上走),自上往下式堆化是调整节点与其左右子节点(往下走)。
1. 从前往后、自下而上式堆化建堆
这里以小顶堆为例,
代码实现:
// 原地建堆
function buildHeap(items, heapSize) {
while(heapSize < items.length - 1) {
heapSize ++
heapify(items, heapSize)
}
}
function heapify(items, i) {
// 自下而上式堆化
while (Math.floor(i/2) > 0 && items[i] < items[Math.floor(i/2)]) {
swap(items, i, Math.floor(i/2)); // 交换
i = Math.floor(i/2);
}
}
function swap(items, i, j) {
let temp = items[i]
items[i] = items[j]
items[j] = temp
}
// 测试
var items = [,5, 2, 3, 4, 1]
// 初始有效序列长度为 1
buildHeap(items, 1)
console.log(items)
// [empty, 1, 2, 3, 5, 4]测试成功
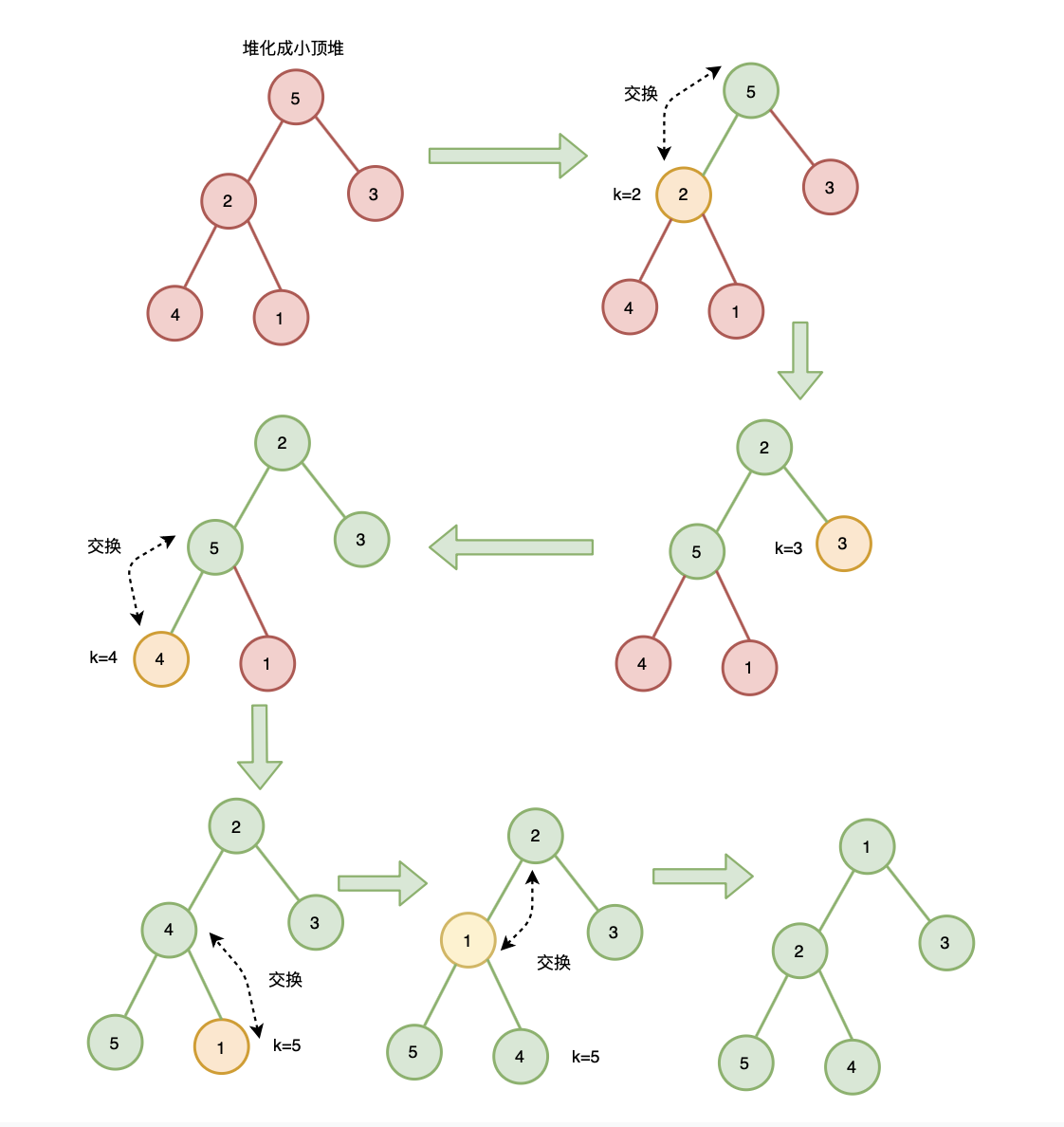
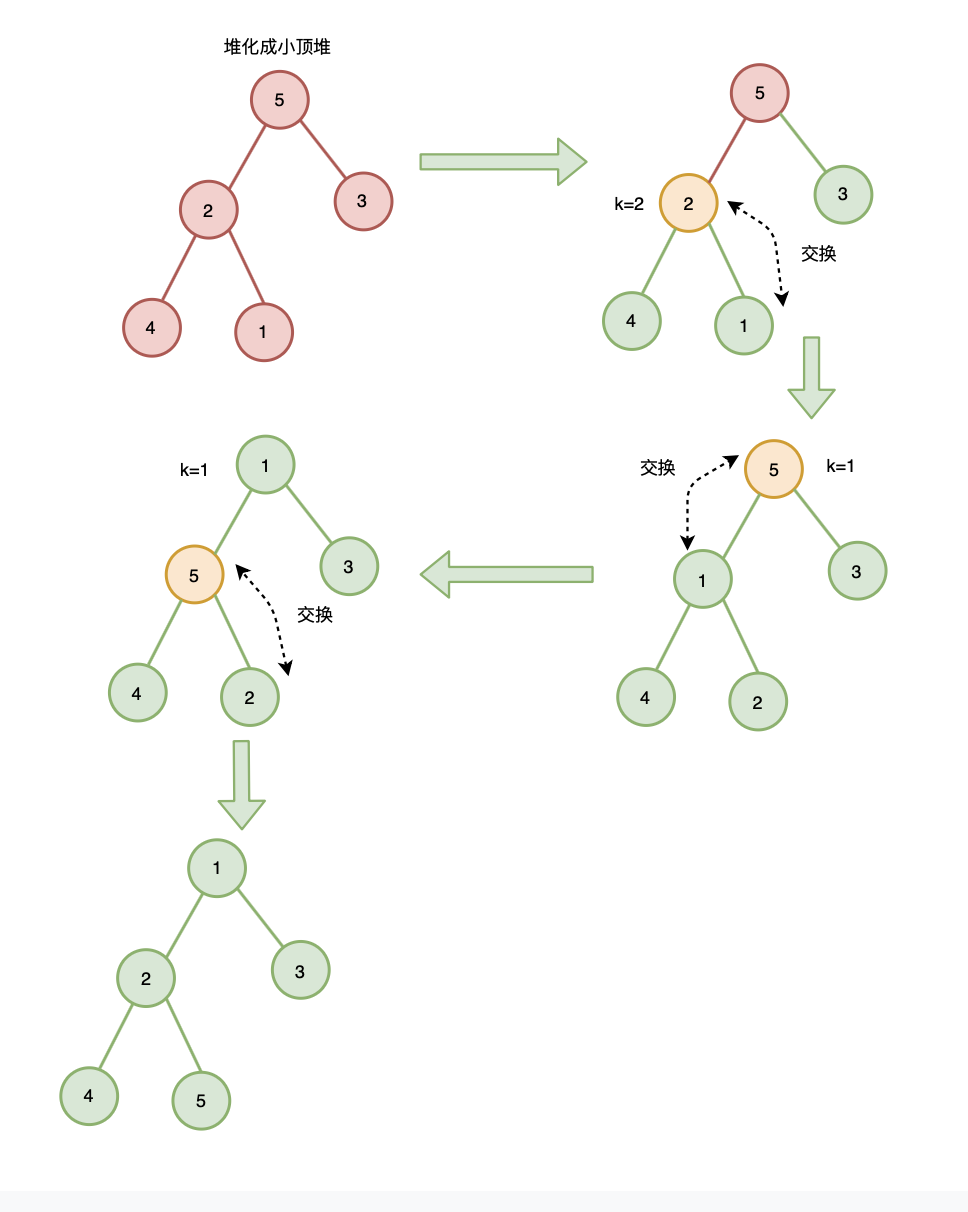
2. 从后往前、自上而下式堆化建堆
这里以小顶堆为例
注意:从后往前并不是从序列的最后一个元素开始,而是从最后一个非叶子节点开始,这是因为,叶子节点没有子节点,不需要自上而下式堆化。
最后一个子节点的父节点为 n/2 ,所以从 n/2 位置节点开始堆化:
代码实现
// 原地建堆
// items: 原始序列
// heapSize: 初始有效序列长度
function buildHeap(items, heapSize) {
// 从最后一个非叶子节点开始,自上而下式堆化
for (let i = Math.floor(heapSize/2); i >= 1; --i) {
heapify(items, heapSize, i);
}
}
function heapify(items, heapSize, i) {
// 自上而下式堆化
while (true) {
var minIndex = i;
if(2*i <= heapSize && items[i] > items[i*2] ) {
minIndex = i*2;
}
if(2*i+1 <= heapSize && items[minIndex] > items[i*2+1] ) {
minIndex = i*2+1;
}
if (minIndex === i) break;
swap(items, i, minIndex); // 交换
i = minIndex;
}
}
function swap(items, i, j) {
let temp = items[i]
items[i] = items[j]
items[j] = temp
}
// 测试
var items = [,5, 2, 3, 4, 1]
// 因为 items[0] 不存储数据
// 所以:heapSize = items.length - 1
buildHeap(items, items.length - 1)
console.log(items)
// [empty, 1, 2, 3, 4, 5]测试成功
五、排序算法:堆排序
1. 原理
堆是一棵完全二叉树,它可以使用数组存储,并且大顶堆的最大值存储在根节点(i=1),所以我们可以每次取大顶堆的根结点与堆的最后一个节点交换,此时最大值放入了有效序列的最后一位,并且有效序列减1,有效堆依然保持完全二叉树的结构,然后堆化,成为新的大顶堆,重复此操作,知道有效堆的长度为 0,排序完成。
完整步骤为:
- 将原序列(n个)转化成一个大顶堆
- 设置堆的有效序列长度为 n
- 将堆顶元素(第一个有效序列)与最后一个子元素(最后一个有效序列)交换,并有效序列长度减1
- 堆化有效序列,使有效序列重新称为一个大顶堆
- 重复以上2步,直到有效序列的长度为 1,排序完成
2. 动图演示
3. 代码实现
function heapSort(items) {
// 构建大顶堆
buildHeap(items, items.length-1)
// 设置堆的初始有效序列长度为 items.length - 1
let heapSize = items.length - 1
for (var i = items.length - 1; i > 1; i--) {
// 交换堆顶元素与最后一个有效子元素
swap(items, 1, i);
// 有效序列长度减 1
heapSize --;
// 堆化有效序列(有效序列长度为 currentHeapSize,抛除了最后一个元素)
heapify(items, heapSize, 1);
}
return items;
}
// 原地建堆
// items: 原始序列
// heapSize: 有效序列长度
function buildHeap(items, heapSize) {
// 从最后一个非叶子节点开始,自上而下式堆化
for (let i = Math.floor(heapSize/2); i >= 1; --i) {
heapify(items, heapSize, i);
}
}
function heapify(items, heapSize, i) {
// 自上而下式堆化
while (true) {
var maxIndex = i;
if(2*i <= heapSize && items[i] < items[i*2] ) {
maxIndex = i*2;
}
if(2*i+1 <= heapSize && items[maxIndex] < items[i*2+1] ) {
maxIndex = i*2+1;
}
if (maxIndex === i) break;
swap(items, i, maxIndex); // 交换
i = maxIndex;
}
}
function swap(items, i, j) {
let temp = items[i]
items[i] = items[j]
items[j] = temp
}
// 测试
var items = [,1, 9, 2, 8, 3, 7, 4, 6, 5]
heapSort(items)
// [empty, 1, 2, 3, 4, 5, 6, 7, 8, 9]测试成功
4. 复杂度分析
**时间复杂度:**建堆过程的时间复杂度是 O(n) ,排序过程的时间复杂度是 O(nlogn) ,整体时间复杂度是 O(nlogn)
空间复杂度: O(1)
六、内存堆与垃圾回收
前端面试高频考察点,瓶子君已经在 栈 章节中介绍过,点击前往 前端进阶算法5:全方位解读前端用到的栈结构(+leetcode刷题)
七、堆的经典应用: Top K 问题(常见于腾讯、字节等面试中)
什么是 Top K 问题?简单来说就是在一组数据里面找到频率出现最高的前 K 个数,或前 K 大(当然也可以是前 K 小)的数。
这种问题我们该怎么处理喃?我们以从数组中取前 K 大的数据为例,可以按以下步骤来:
- 从数组中取前
K个数,构造一个小顶堆 - 从
K+1位开始遍历数组,每一个数据都和小顶堆的堆顶元素进行比较,如果小于堆顶元素,则不做任何处理,继续遍历下一元素;如果大于堆顶元素,则将这个元素替换掉堆顶元素,然后再堆化成一个小顶堆。 - 遍历完成后,堆中的数据就是前 K 大的数据
遍历数组需要 O(N) 的时间复杂度,一次堆化需要 O(logK) 时间复杂度,所以利用堆求 Top K 问题的时间复杂度为 O(NlogK)。
利用堆求 Top K 问题的优势
也许很多人会认为,这种求 Top K 问题可以使用排序呀,没必要使用堆呀
其实是可以使用排序来做的,将数组进行排序(可以是最简单的快排),去前 K 个数就可以了,so easy
但当我们需要在一个动态数组中求 Top K 元素怎么办喃,动态数组可能会插入或删除元素,难道我们每次求 Top K 问题的时候都需要对数组进行重新排序吗?那每次的时间复杂度都为 O(NlogN)
这里就可以使用堆,我们可以维护一个 K 大小的小顶堆,当有数据被添加到数组中时,就将它与堆顶元素比较,如果比堆顶元素大,则将这个元素替换掉堆顶元素,然后再堆化成一个小顶堆;如果比堆顶元素小,则不做处理。这样,每次求 Top K 问题的时间复杂度仅为 O(logK)
八、堆的经典应用:中位数问题
除了 Top K 问题,堆还有一个经典的应用场景就是求中位数问题
中位数,就是处于中间的那个数:
[1, 2, 3, 4, 5] 的中位数是 3
[1, 2, 3, 4, 5, 6] 的中位数是 3, 4
即:
当 n % 2 !== 0 时,中位数为:arr[(n-1)/2]
当 n % 2 === 0 时,中位数为:arr[n/2], arr[n/2 + 1]
如何利用堆来求解中位数问题喃?
这里需要维护两个堆:
- 大顶堆:用来存取前 n/2 个小元素,如果 n 为奇数,则用来存取前
Math.floor(n/2) + 1个元素 - 小顶堆:用来存取后 n/2 个大元素
那么,中位数就为:
- n 为奇数:中位数是大顶堆的堆顶元素
- n 为偶数:中位数是大顶堆的堆顶元素与小顶堆的堆顶元素
当数组为动态数组时,每当数组中插入一个元素时,都需要如何调整堆喃?
如果插入元素比大顶堆的堆顶要大,则将该元素插入到小顶堆中;如果要小,则插入到大顶堆中。
当出入完后后,如果大顶堆、小顶堆中元素的个数不满足我们已上的要求,我们就需要不断的将大顶堆的堆顶元素或小顶堆的堆顶元素移动到另一个堆中,直到满足要求
由于插入元素到堆、移动堆顶元素都需要堆化,所以,插入的时间复杂度为 O(logN) ,每次插入完成后求中位数仅仅需要返回堆顶元素即可,时间复杂度为 O(1)
中位数的变形:TP 99 问题
TP 99 问题:指在一个时间段内(如5分钟),统计某个方法(或接口)每次调用所消耗的时间,并将这些时间按从小到大的顺序进行排序,取第 99% 的那个值作为 TP99 值;
例如某个接口在 5 分钟内被调用了100次,每次耗时从 1ms 到 100ms之间不等数据,将请求耗时从小到大排列,TP99 就是取第 100*0.99 = 99 次请求耗时 ,类似地 TP50、TP90,TP99越小,说明这个接口的性能越好
所以,针对 TP99 问题,我们同样也可以维护两个堆,一个大顶堆,一个小顶堆。大顶堆中保存前 99% 个数据,小顶堆中保存后 1% 个数据。大顶堆堆顶的数据就是我们要找的 99% 响应时间。
本小节参考极客时间的:数据结构与算法之美
九、总结
堆是一个完全二叉树,并且堆上的任意节点值都必须大于等于(大顶堆)或小于等于(小顶堆)其左右子节点值,推可以采用数组存储法存储,可以通过插入式建堆或原地建堆,堆的重要应用有:
- 推排序
- Top K 问题:堆化,取前 K 个元素
- 中位数问题:维护两个堆,一大(前50%)一小(后50%),奇数元素取大顶堆的堆顶,偶数取取大、小顶堆的堆顶
JavaScript 的存储机制分为代码空间、栈空间以及堆空间,代码空间用于存放可执行代码,栈空间用于存放基本类型数据和引用类型地址,堆空间用于存放引用类型数据,当调用栈中执行完成一个执行上下文时,需要进行垃圾回收该上下文以及相关数据空间,存放在栈空间上的数据通过 ESP 指针来回收,存放在堆空间的数据通过副垃圾回收器(新生代)与主垃圾回收器(老生代)来回收。
十、leetcode刷题:最小的k个数
话不多说,来一道题目加深一下理解吧:
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
示例 1:
输入:arr = [3,2,1], k = 2
输出:[1,2] 或者 [2,1]示例 2:
输入:arr = [0,1,2,1], k = 1
输出:[0]限制:
0 <= k <= arr.length <= 100000 <= arr[i] <= 10000
题目详情已提交到 #59 ,欢迎解答,欢迎star
对于我这个对二叉树、堆排序完全外行的人,遇到的一些问题,我参考了很多文章后发现的:
1,从前往后、自下而上式堆化建堆,找到的这个根节点,您没解释清楚怎么找到这个根节点,您的图中就直接是k=2了,为啥从这个节点开始找,完全没说。
2,”最后一个子节点的父节点为 n/2 ,所以从 n/2 位置节点开始堆化:“,为啥最后一个子节点的父节点是n/2,完全没解释。是不是有个定义是这么写的?完全没说,然后就开始下面的了。此时我内心:先这么记着吧,要不然你还能把作者找出来问问呀?
此时我继续看图,结果图中就只有”交换“,为啥要这么交换,完全没说。交换的条件是啥,为啥,完全不解释。我内心:先这么记着吧,作者说要交换那就交换吧。(之所以比较纠结,因为图中,当前节点一会儿跟子节点比较交换,一会儿有去找父节点比较交换,有个原则不行吗,比如说,先找子再找父,你只要说了这个原则,那我就马上懂了,可是你也没说啊,我只能猜了)
类似的这种,我感觉有些模糊的地方有点多,导致我就看不下去了。。。。
@woaixiangbao 你的疑惑来源于你对完全二叉树的基本性质不熟悉。你可以尝试自己用一个数组来表示一下完全二叉树,然后找几个节点观察一下,就会发现完全二叉树的父子节点的位置是有规律的,至于这个规律是什么,可以记住,也可以不记,大不了用到的时候写个简单的二叉树推一下。
堆排序推荐看这个视频https://www.bilibili.com/video/BV1Eb41147dK?from=search&seid=16051892050619509521&spm_id_from=333.337.0.0
讲解的很好,我有好多疑惑看了之后都弄懂了
我看了好几篇文章,都是说左边的孩子的i值计算是这样的:
跟你的2*i 不一样,怎么回事?
你把根节点用arr索引标记时标记索引为0,即你把arr[0]放到根节点,那么这个堆里根节点的索引为 i ,则根节点的左子节点的索引与根节点索引的关系就是=2i+1 ,当你把根节点用arr索引标记时标记索引为1,那么这个堆里根节点的索引为 i ,则根节点的左子节点的索引与根节点索引的关系就是=2i , 你自己画个堆的完全二叉树结构然后给它用索引标记一下看下过程就能很容易看出来根与左右子节点索引方面的对应关系的。一种情况就是你说的根节点填的是索引0, 上面层主给的解法中,它往根节点填的索引是1 。可以很容易看出来对应关系的,这个没有特别的科学依据,无厘头的,看出来的。
大根堆的基础知识网上搜了一个,如下文章:
https://blog.csdn.net/m0_59356888/article/details/125444573
它heapify 那个函数里为啥用 2i表示节点i的左子节点,2i+1表示节点i的右子节点。很明显 , i 指的是在数组里的索引,我们回想这个数组填满堆的顺序是从顶层往下层,每层从左往右依次填满,他们每个节点的值对应的在数组里的索引就是(0, 1, 2, 。。。或者就是1,2,3,...或者就是2,3,4,....。反正填满这个堆结构用到的这些arr[i],i 得是连续的,索引依次增加 1 )然后现在这个答案中堆顶部根它填充的是索引1,则根下面一层(即第二层)的索引是2和3,第三层的索引是4,5,6,7。此时依次按照索引递增然后从上层到下层,每层从左到右填下去,会发现,它里面任意拿出一个二叉结构(比如(1,2,3))的根节点索引是i,它左子节点的索引就是2i ,而它右子节点的索引就是2i+1 (就是比2*i 多 1,毕竟用数组里的值填充堆的过程是从上往下,从左往右挨着填充的。 )。
我看了好几篇文章,都是说左边的孩子的i值计算是这样的:
跟你的2*i 不一样,怎么回事?
分隔线*******
关于 “最小的k个数” 这道题,给你个解法:
/**
-
@param {number[]} arr
-
@param {number} k
-
@return {number[]}
*/
function swap(arr, i , j){
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// 堆化
function heapify(arr, n, i){
// n 代表这颗树里面有n个节点。
// i 代表要对第i个节点做堆化操作
// 自上而下式堆化if(i>=n){
return ;
}
let maxindex = i;
let c1 = 2i+1; //左子节点的值对应arr中的索引
let c2 = 2i+2; //右子节点的值对应arr中的索引if(c1<n && arr[c1]>arr[i]){
maxindex = c1;
}
if(c2<n && arr[c2]>arr[maxindex]){
maxindex = c2;
}
if(maxindex !== i){
swap(arr, maxindex, i);heapify(arr, n, maxindex);}
}
// 原地建堆,从后往前,自上而下式建大顶堆(顶元素是堆中最大的。)
function build_heap(arr, n){
let lastnode = n-1; // 堆数组的最后一个值的索引
let lastparent = Math.floor((lastnode-1)/2);
// 从最后一个非叶子节点开始,自上而下式堆化
for(let i = lastparent; i>=0; i--){
heapify(arr, n, i);
}
}
var getLeastNumbers = function(arr, k) {
let heap = [];
// 从 arr 中取出前 k 个数,构建一个大顶堆
for(let i=0; i<k; i++){
heap.push(arr[i]);
}
build_heap(heap, k);
for(let i= k; i<arr.length; i++){
if(arr[i]<heap[0]){
// 替换堆顶元素并堆化(自顶而下)
heap[0] = arr[i];
heapify(heap, k, 0);
}
}
return heap;
};
class Solution {
public:
void maxHeapify(vector& a, int i, int heapSize) {
int l = i * 2 + 1, r = i * 2 + 2, largest = i;
if (l < heapSize && a[l] > a[largest]) {
largest = l;
}
if (r < heapSize && a[r] > a[largest]) {
largest = r;
}
if (largest != i) {
swap(a[i], a[largest]);
maxHeapify(a, largest, heapSize);
}
}
void buildMaxHeap(vector<int>& a, int heapSize) {
for (int i = heapSize / 2; i >= 0; --i) {
maxHeapify(a, i, heapSize);
}
}
int findKthLargest(vector<int>& nums, int k) {
int heapSize = nums.size();
buildMaxHeap(nums, heapSize);
for (int i = nums.size() - 1; i >= nums.size() - k + 1; --i) {
swap(nums[0], nums[i]);
--heapSize;
maxHeapify(nums, 0, heapSize);
}
return nums[0];
}
};
这段代码中的maxHeapify是不是没有必要加递归?
class Solution { public: void maxHeapify(vector& a, int i, int heapSize) { int l = i * 2 + 1, r = i * 2 + 2, largest = i; if (l < heapSize && a[l] > a[largest]) { largest = l; } if (r < heapSize && a[r] > a[largest]) { largest = r; } if (largest != i) { swap(a[i], a[largest]); maxHeapify(a, largest, heapSize); } }
void buildMaxHeap(vector<int>& a, int heapSize) { for (int i = heapSize / 2; i >= 0; --i) { maxHeapify(a, i, heapSize); } } int findKthLargest(vector<int>& nums, int k) { int heapSize = nums.size(); buildMaxHeap(nums, heapSize); for (int i = nums.size() - 1; i >= nums.size() - k + 1; --i) { swap(nums[0], nums[i]); --heapSize; maxHeapify(nums, 0, heapSize); } return nums[0]; }}; 这段代码中的maxHeapify是不是没有必要加递归?
为什么加递归?我认为是:为了自顶向下都筛选一遍,如果不加递归那一句,代码就只比较了root和root的两个子节点。实际上,如果root值是最大或者最小的,它应该从该完全二叉树的顶部开始一次次向下交换位置,直到位置换到该完全二叉树的底部。