Sequence Alignment Problem

The dynamic programming approach is used in the basic version of sequence alignment problem solution.
The combination of divide and conquer, and dynamic programming is used in the efficient version of the sequence alignment algorithm.
Here, the problem is divided into sub problems and solve them recursively.
In each subproblem, The string X is split into half and the position y_split_pos is calculated by memory efficient version of sequence alignment to split Y string.
Finally, the base case is to find out the alignment when length of X and Y is less than or equal to 2.

Time Complexity: O(m*n)
Space Complexity: O(m*n)

Time Complexity: O(m*n)
Space Complexity: O(m+n)

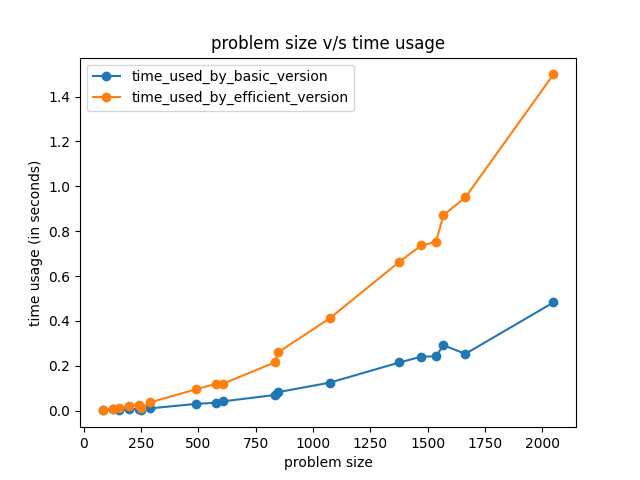
Time taken by efficient version is higher than the basic version of sequence alignment algorithm.
The overhead of recursion for divide and conquer, as well as the overhead for finding y_split_pos for Y string causes the time. for efficient algorithm to be little greater than basic version which contains only m*n iterations.
Therefore, the overhead associated with the efficient algorithm causes the time to be a bit greater than the basic version.

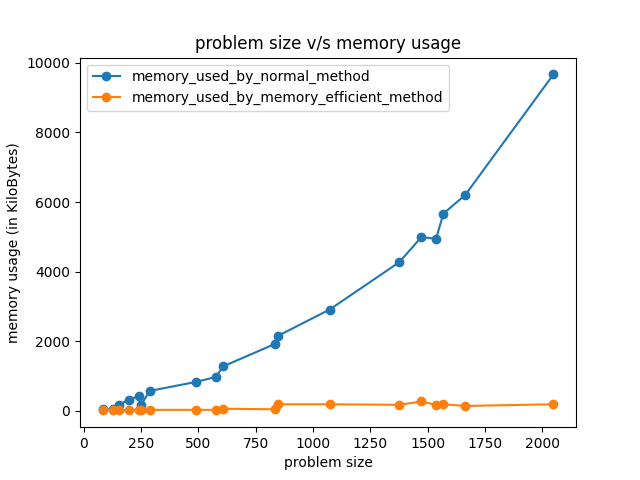
The efficient algorithm uses 2*k (k being the size of Y string) array to calculate the minimum sequence alignment for every recursion in divide_and_conquer method. Hence, the max memory allocated will be less than 2*n (n is the max size of string Y).
Whereas, in case of basic version, the memory allocated is m*n, which causes the memory size to increase linearly proportional to the input size.

sk112/sequence_alignment_problem